本稿には、2023年に実施された統計検定1級『統計数理』 問2の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。
- 著作権の関係上、問題文は、掲載することができません。申し訳ありませんが、閲覧者のみなさまでご用意いただければ幸いです。
- この答案は、あくまでも筆者が自作したものであり、公式なものではありません。正式な答案については、公式問題集をご参照ください。
- 計算ミスや誤字・脱字などがありましたら、コメントなどでご指摘いただければ大変助かります。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
〔1〕カイ2乗分布の確率密度関数の概形
与えられた確率密度関数に $k=1,2,3$ を代入すると、$0 \le y$ の範囲において、 \begin{align} f_1 \left(y\right)=\frac{1}{2^\frac{1}{2}\Gamma \left(\frac{1}{2}\right)}y^{-\frac{1}{2}}e^{-\frac{y}{2}}=\frac{1}{\sqrt{2\pi}}\frac{1}{\sqrt y}e^{-\frac{y}{2}}\\ f_2 \left(y\right)=\frac{1}{2\Gamma \left(1\right)}y^0e^{-\frac{y}{2}}=\frac{1}{2}e^{-\frac{y}{2}}\\ f_3 \left(y\right)=\frac{1}{2^\frac{3}{2}\Gamma \left(\frac{3}{2}\right)}y^\frac{1}{2}e^{-\frac{y}{2}}=\frac{1}{\sqrt{2\pi}}\sqrt y e^{-\frac{y}{2}} \end{align} それぞれの1階微分を求めると、 \begin{align} f_1^\prime \left(y\right)&=\frac{1}{\sqrt{2\pi}} \left(e^{-\frac{y}{2}} \cdot \frac{1}{dy}y^{-\frac{1}{2}}+y^{-\frac{1}{2}} \cdot \frac{1}{dy}e^{-\frac{y}{2}}\right)\\ &=\frac{1}{\sqrt{2\pi}} \left(-\frac{1}{2}y^{-\frac{3}{2}}e^{-\frac{y}{2}}-\frac{1}{2}y^{-\frac{1}{2}}e^{-\frac{y}{2}}\right)\\ &=-\frac{1}{2\sqrt{2\pi}}\frac{1}{\sqrt y}e^{-\frac{y}{2}} \left(\frac{1}{y}+1\right) \end{align} \begin{align} f_2^\prime \left(y\right)=-\frac{1}{4}e^{-\frac{y}{2}} \end{align} \begin{align} f_3^\prime \left(y\right)&=\frac{1}{\sqrt{2\pi}} \left(e^{-\frac{y}{2}} \cdot \frac{1}{dy}y^\frac{1}{2}+y^\frac{1}{2} \cdot \frac{1}{dy}e^{-\frac{y}{2}}\right)\\ &=\frac{1}{\sqrt{2\pi}} \left(\frac{1}{2}y^{-\frac{1}{2}}e^{-\frac{y}{2}}-\frac{1}{2}y^\frac{1}{2}e^{-\frac{y}{2}}\right)\\ &=\frac{1}{2\sqrt{2\pi}}e^{-\frac{y}{2}} \left(\frac{1}{\sqrt y}-\sqrt y\right) \end{align} 増減表は、 \begin{array}{c|ccccc} y & 0 & \cdots & 1 & \cdots \\ \hline f_1^\prime \left(y\right) & -\infty & - & - & - \\ \hline f_1 \left(y\right) & \infty & \searrow & \frac{1}{\sqrt{2\pi e}} & \searrow \\ \hline f_2^\prime \left(y\right) & 0 & - & - & - \\ \hline f_2 \left(y\right) & \frac{1}{2} & \searrow & \frac{1}{\sqrt e} & \searrow \\ \hline f_3^\prime \left(y\right) & \infty & + & 0 & - \\ \hline f_3 \left(y\right) & 0 & \nearrow & \frac{\sqrt e}{\sqrt{2\pi}} & \searrow \\ \hline \end{array} グラフの概形を描くと、以下のようになる。 $\blacksquare$
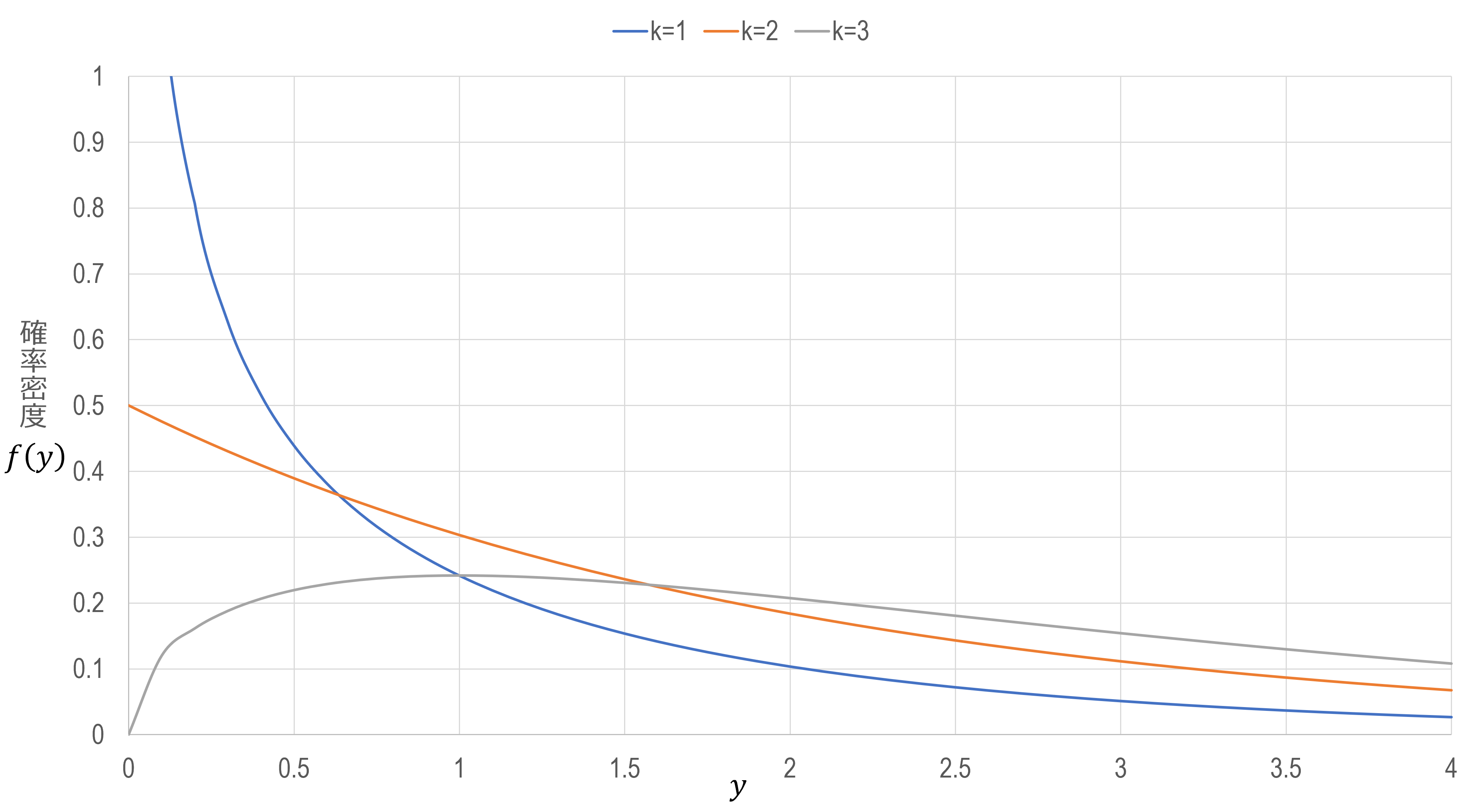
〔2〕確率変数変換
以下のように変数変換すると、 \begin{align} \left\{\begin{matrix}x=\frac{z}{\sqrt{y_1}}&-\infty \lt x \lt \infty\\s=y_1&0 \lt s \lt \infty\\\end{matrix}\right.\Rightarrow \left\{\begin{matrix}z=x\sqrt s&-\infty \lt z \lt \infty\\y_1=s&0 \lt y_1 \lt \infty\\\end{matrix}\right. \end{align} 変数変換のヤコビアンは、 \begin{align} J&= \left|\begin{matrix}\frac{\partial z}{\partial x}&\frac{\partial y_1}{\partial x}\\\frac{\partial z}{\partial s}&\frac{\partial y_1}{\partial s}\\\end{matrix}\right|\\ &= \left|\begin{matrix}\sqrt s&0\\\frac{x}{2\sqrt s}&1\\\end{matrix}\right|\\ &=\sqrt s \end{align} このとき、$x,s$ の同時確率密度関数 $f_{X,S} \left(x,s\right)=f \left\{z \left(x,s\right),y_1 \left(x,s\right)\right\} \left|J\right|$ は、 \begin{align} f_{X,S} \left(x,s\right)&=\varphi \left(x\sqrt s\right) \cdot f_1 \left(s\right) \cdot \sqrt s\\ &=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2s}{2}} \cdot \frac{1}{\sqrt{2\pi}}\frac{1}{\sqrt s}e^{-\frac{s}{2}} \cdot \sqrt s\\ &=\frac{1}{2\pi}e^{-\frac{s}{2} \left(1+x^2\right)} \end{align} よって、周辺確率密度関数の定義式 $f \left(x\right)=\int_{-\infty}^{\infty}f \left(x,s\right)ds$ より、$X$ の周辺確率密度関数は、 \begin{align} g \left(x\right)&=\int_{0}^{\infty}{\frac{1}{2\pi}e^{-\frac{s}{2} \left(1+x^2\right)}ds}\\ &=\frac{1}{2\pi} \left[-\frac{2}{1+x^2}e^{-\frac{s}{2} \left(1+x^2\right)}\right]_0^\infty\\ &=\frac{1}{\pi \left(1+x^2\right)} \left\{0- \left(-1\right)\right\}\\ &=\frac{1}{\pi \left(1+x^2\right)} \end{align} $\blacksquare$
〔3〕変数変換後の確率密度関数
確率変数 $X,W$ の関係は、 \begin{gather} W=\tan^{-1}{X}\Leftrightarrow X=\tan{W}\\ -\frac{\pi}{2} \lt w \lt \frac{\pi}{2}\Leftrightarrow-\infty \lt x \lt \infty \end{gather} 変数変換後の確率密度関数の公式 $g \left(y\right)=f \left[h^{-1} \left(y\right)\right] \left|\frac{d}{dy}h^{-1} \left(y\right)\right|$ より、 \begin{align} h \left(w\right)&=\frac{1}{\pi \left(1+\tan^2{w}\right)} \cdot \frac{d}{dw}\tan{w}\\ &=\frac{1}{\pi} \cdot \frac{1}{\frac{\cos^2{w}+\sin^2{w}}{\cos^2{w}}} \cdot \frac{1}{\cos^2{w}}\\ &=\frac{1}{\pi} \cdot \cos^2{w} \cdot \frac{1}{\cos^2{w}}\\ &=\frac{1}{\pi} \end{align} これは、区間 $ \left(-\frac{\pi}{2},\frac{\pi}{2}\right)$ の一様分布の確率密度関数である。 $\blacksquare$
〔4〕乱数の生成法
これは、区間 $ \left(0,1\right)$ 上の一様分布に従う乱数 $U_1,\ U_2,\ \cdots $ を \begin{align} \pi \left(U_1-0.5\right),\ \pi \left(U_2-0.5\right),\ \cdots \end{align} とし、 \begin{align} X_1=\tan{ \left\{\pi \left(U_1-0.5\right)\right\}},\ X_2=\tan{ \left\{\pi \left(U_2-0.5\right)\right\}},\ \cdots \end{align} とすればよい。 $\blacksquare$



0 件のコメント:
コメントを投稿