本稿には、2021年に実施された統計検定1級『医薬生物学』 問1の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。
- 著作権の関係上、問題文は、掲載することができません。申し訳ありませんが、閲覧者のみなさまでご用意いただければ幸いです。
- この答案は、あくまでも筆者が自作したものであり、公式なものではありません。正式な答案については、公式問題集をご参照ください。
- 計算ミスや誤字・脱字などがありましたら、コメントなどでご指摘いただければ大変助かります。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
〔1〕イベント確率密度関数と生存関数・ハザード関数の関係
条件付き確率の定義より、 \begin{align} \lambda \left(t\right)&=\lim_{\Delta t\rightarrow0}{\frac{1}{\Delta t}}P \left(t \le T \le t+\Delta t\middle| t \le T\right)\\ &=\lim_{\Delta t\rightarrow0}{\frac{1}{\Delta t}\frac{P \left(t \le T \le t+\Delta t,t \le T\right)}{P \left(t \le T\right)}}\\ &=\lim_{\Delta t\rightarrow0}{\frac{P \left(t \le T \le t+\Delta t\right)}{\Delta t}\frac{1}{P \left(t \le T\right)}} \end{align} 生存関数の定義 $S \left(t\right)=P \left(t \le T\right)$ より、 \begin{align} \lambda \left(t\right)=\lim_{\Delta t\rightarrow0}{\frac{P \left(t \le T \le t+\Delta t\right)}{\Delta t}\frac{1}{S \left(t\right)}} \end{align} イベント確率の分布関数の定義より、 \begin{align} \lambda \left(t\right)=\lim_{\Delta t\rightarrow0}{\frac{F \left(t+\Delta t\right)-F \left(t\right)}{\Delta t}\frac{1}{S \left(t\right)}} \end{align} 微分の定義と分布関数と確率密度関数の関係より、 \begin{gather} \lambda \left(t\right)=\frac{1}{S \left(t\right)} \cdot \frac{d}{dt}F \left(t\right)=\frac{f \left(t\right)}{S \left(t\right)}\\ f \left(t\right)=\lambda \left(t\right) \cdot S \left(t\right) \end{gather} $\blacksquare$
〔2〕カプラン・マイヤー法による生存関数の推定
カプラン・マイヤー法により生存関数を推定すると以下のようになる。
| 経過時間
$t_i$ | リスク集合
$n_i$ | イベント数
$d_i$ | 打ち切り数
$c_i$ | 生存者数
$s_i$ | 生存関数
$\hat{S} \left(t_i\right)$ | 生存関数
$1-\hat{S} \left(t_i\right)$ |
|---|---|---|---|---|---|---|
| $4$ | $8$ | $0$ | $1$ | $8-0=8$ | $\frac{8}{8}=1$ | $1-1=0$ |
| $6$ | $7$ | $0$ | $1$ | $7-0=7$ | $1\times\frac{7}{7}=1$ | $1-1=0$ |
| $8$ | $6$ | $0$ | $1$ | $6-0=6$ | $1\times\frac{6}{6}=1$ | $1-1=0$ |
| $10$ | $5$ | $1$ | $0$ | $5-1=4$ | $1\times\frac{4}{5}=\frac{4}{5}$ | $1-\frac{4}{5}=\frac{1}{5}$ |
| $12$ | $4$ | $1$ | $0$ | $4-1=3$ | $\frac{4}{5}\times\frac{3}{4}=\frac{3}{5}$ | $1-\frac{3}{5}=\frac{2}{5}$ |
| $14$ | $3$ | $1$ | $0$ | $3-1=2$ | $\frac{3}{5}\times\frac{2}{3}=\frac{2}{5}$ | $1-\frac{2}{5}=\frac{3}{5}$ |
| $16$ | $2$ | $0$ | $1$ | $2-0=2$ | $\frac{2}{5}\times\frac{2}{2}=\frac{2}{5}$ | $1-\frac{2}{5}=\frac{3}{5}$ |
| $18$ | $1$ | $1$ | $0$ | $1-1=0$ | $\frac{2}{5}\times\frac{0}{1}=0$ | $1-0=1$ |
グラフを描くと、以下のようになる。
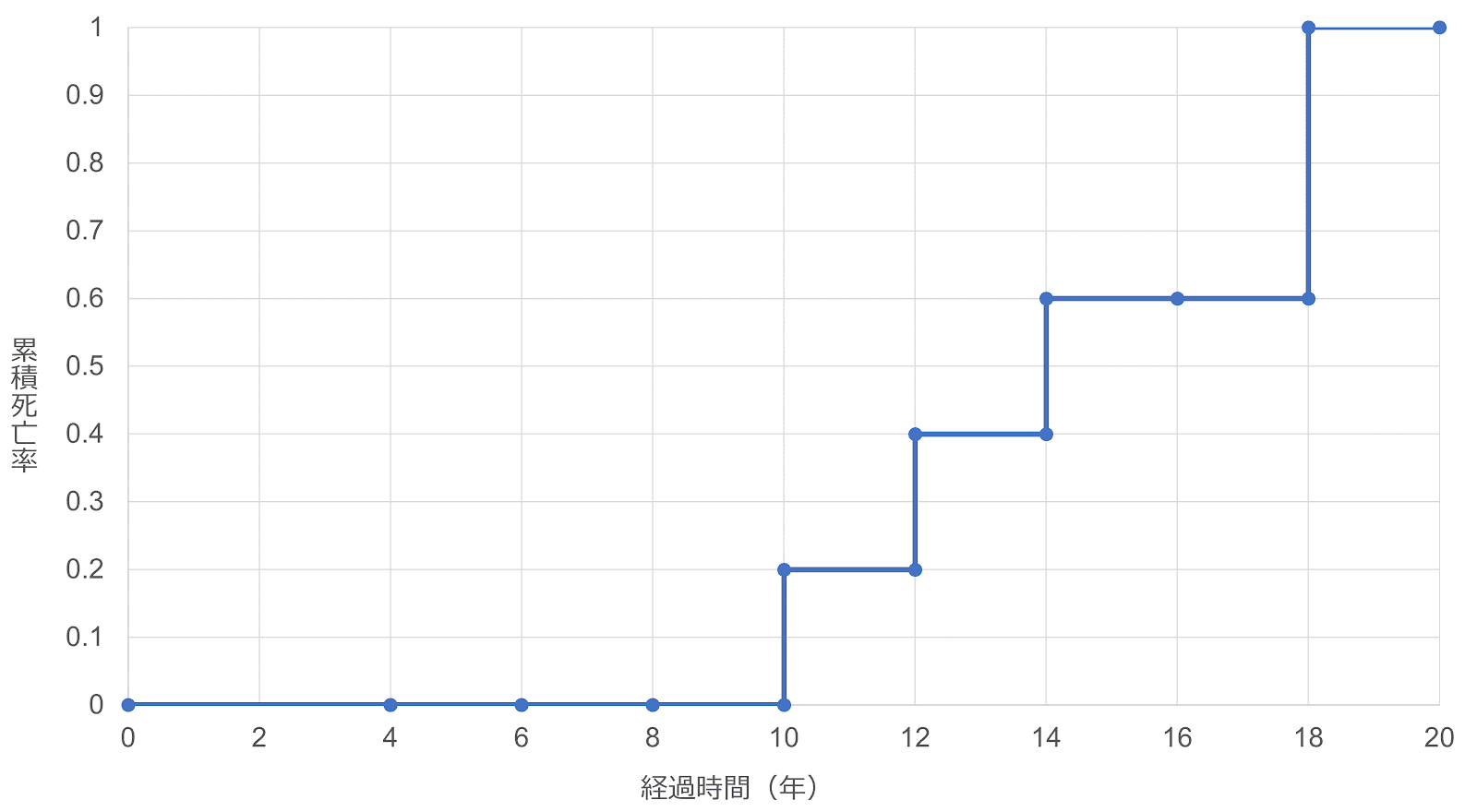
〔3〕イベントごとの累積イベント発現関数の導出
〔1〕の結果より、 \begin{gather} f_1 \left(t\right)=\lambda_1 \left(t\right) \cdot S_2 \left(t\right)\\ f_2 \left(t\right)=\lambda_2 \left(t\right) \cdot S_2 \left(t\right) \end{gather} 分布関数と確率密度関数の関係より、 \begin{gather} F_1 \left(t\right)=\int_{0}^{t}{\lambda_1 \left(u\right) \cdot S_2 \left(u\right)du}\\ F_2 \left(t\right)=\int_{0}^{t}{\lambda_2 \left(u\right) \cdot S_2 \left(u\right)du} \end{gather} $\blacksquare$
〔4〕イベントごとの累積イベント発現関数の推定
問題文の定義に沿って各値を算出すると以下のようになる。
| $t_i$ | $j$ | $t_{ji}$ | $d_{1i}$ | $d_{2i}$ | $n_{ji}$ | ${\hat{S}}_2 \left(t_{ji}\right)$ | ${\hat{S}}_2 \left(t_{ji}^-\right)$ | ${\hat{F}}_1 \left(t\right)$ | ${\hat{F}}_2 \left(t\right)$ |
|---|---|---|---|---|---|---|---|---|---|
| $0$ | ― | ― | $0$ | $0$ | $8$ | $\frac{8}{8}=1$ | $1$ | $\frac{0}{8}\times1=0$ | $\frac{0}{8}\times1=0$ |
| $4$ | $2$ | $t_{21}$ | $0$ | $1$ | $8$ | $1\times\frac{7}{8}=\frac{7}{8}$ | $1$ | $0+\frac{0}{8}\times1=0$ | $0+\frac{1}{8}\times1=\frac{1}{8}$ |
| $6$ | $2$ | $t_{22}$ | $0$ | $1$ | $7$ | $\frac{7}{8}\times\frac{6}{7}=\frac{3}{4}$ | $\frac{7}{8}$ | $0+\frac{0}{7}\times\frac{7}{8}=0$ | $\frac{1}{8}+\frac{1}{7}\times\frac{7}{8}=\frac{1}{4}$ |
| $8$ | $0$ | ― | $0$ | $0$ | $6$ | $\frac{3}{4}\times\frac{6}{6}=\frac{3}{4}$ | $\frac{3}{4}$ | $0+\frac{0}{6}\times\frac{3}{4}=0$ | $\frac{1}{4}+\frac{0}{6}\times\frac{3}{4}=\frac{1}{4}$ |
| $10$ | $1$ | $t_{11}$ | $1$ | $0$ | $5$ | $\frac{3}{4}\times\frac{4}{5}=\frac{3}{5}$ | $\frac{3}{4}$ | $0+\frac{1}{5}\times\frac{3}{4}=\frac{3}{20}$ | $\frac{1}{4}+\frac{0}{5}\times\frac{3}{4}=\frac{1}{4}$ |
| $12$ | $1$ | $t_{12}$ | $1$ | $0$ | $4$ | $\frac{3}{5}\times\frac{3}{4}=\frac{9}{20}$ | $\frac{3}{5}$ | $\frac{3}{20}+\frac{1}{4}\times\frac{3}{5}=\frac{3}{10}$ | $\frac{1}{4}+\frac{0}{4}\times\frac{3}{5}=\frac{1}{4}$ |
| $14$ | $1$ | $t_{13}$ | $1$ | $0$ | $3$ | $\frac{9}{20}\times\frac{2}{3}=\frac{3}{10}$ | $\frac{9}{20}$ | $\frac{3}{10}+\frac{1}{3}\times\frac{9}{20}=\frac{9}{20}$ | $\frac{1}{4}+\frac{0}{3}\times\frac{9}{20}=\frac{1}{4}$ |
| $16$ | $0$ | ― | $0$ | $0$ | $2$ | $\frac{3}{10}\times\frac{2}{2}=\frac{3}{10}$ | $\frac{3}{10}$ | $\frac{9}{20}+\frac{0}{2}\times\frac{3}{10}=\frac{9}{20}$ | $\frac{1}{4}+\frac{0}{2}\times\frac{3}{10}=\frac{1}{4}$ |
| $18$ | $1$ | $t_{14}$ | $1$ | $0$ | $1$ | $\frac{3}{10}\times\frac{0}{1}=0$ | $\frac{3}{10}$ | $\frac{9}{20}+\frac{1}{1}\times\frac{3}{10}=\frac{3}{4}$ | $\frac{1}{4}+\frac{0}{1}\times\frac{3}{10}=\frac{1}{4}$ |
したがって、(あ)6(い)5(う)0.15(え)0.75(お)0.125(か)0.25 $\blacksquare$
〔5〕競合リスクに対する考慮の有無の比較
グラフを描くと、以下のようになる。
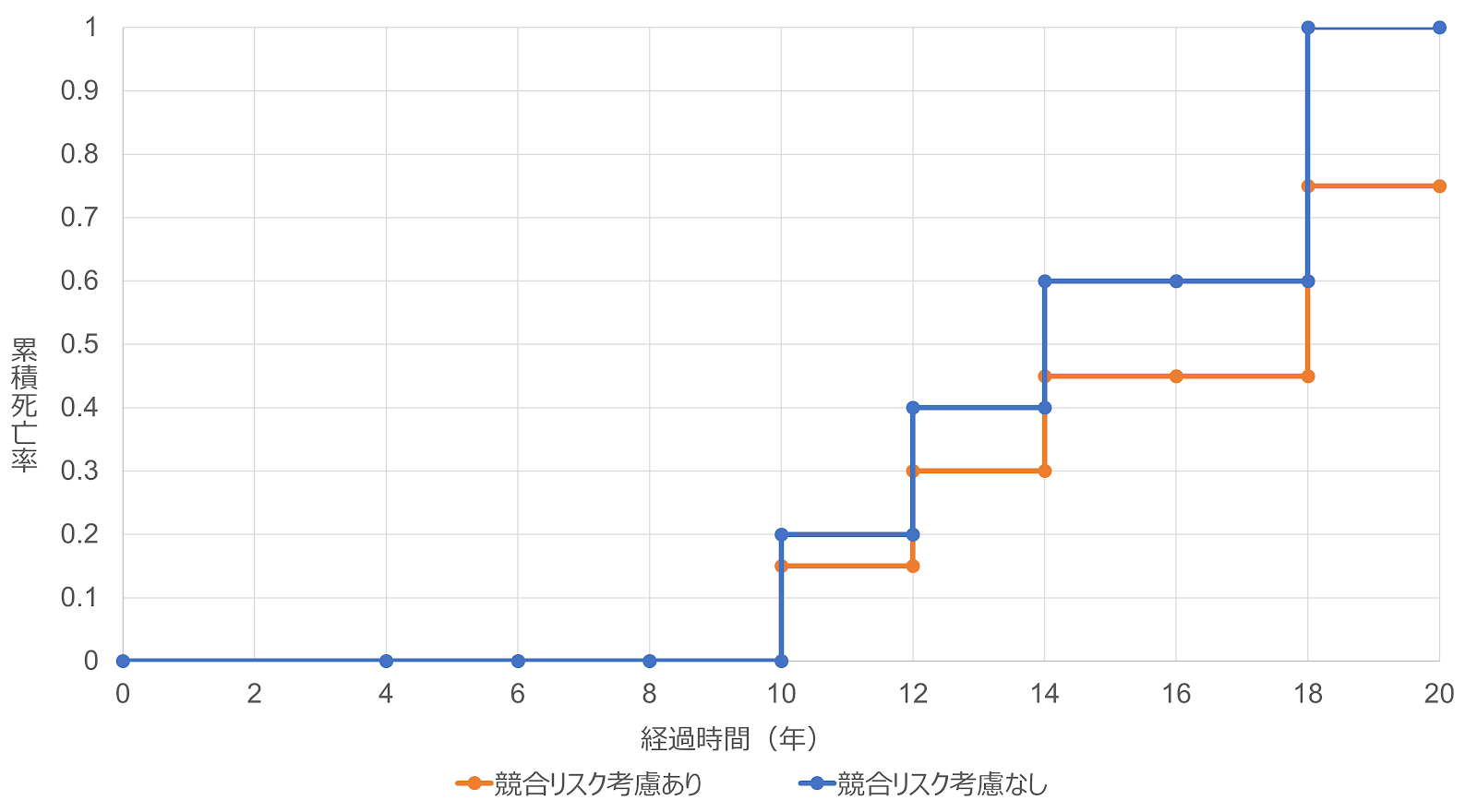
(競合リスクに対する考慮の有無の比較)



0 件のコメント:
コメントを投稿