本稿には、2024年に実施された統計検定1級『統計数理』 問4の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。
- 統計検定の問題の使用に関する規約により禁止されているため、問題文は掲載することができません。公式サイトで公開されているものなどをご参照ください。
- この答案は、あくまでも筆者が自作したものであり、公式なものではありません。正式な答案については、公式問題集をご参照ください。
- 計算ミスや誤字・脱字などがありましたら、コメントなどでご指摘いただければ大変助かります。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
〔1〕経験分布関数(累積度数分布)
得られたデータに対する度数分布表と経験分関数のグラフを書くと、それぞれ以下のようになる。 $\blacksquare$
| $x$ | 度数 | 累積相対度数 |
|---|---|---|
| $1$ | $1$ | $\frac{1}{5}$ |
| $2$ | $2$ | $\frac{3}{5}$ |
| $3$ | $1$ | $\frac{4}{5}$ |
| $6$ | $1$ | $1$ |
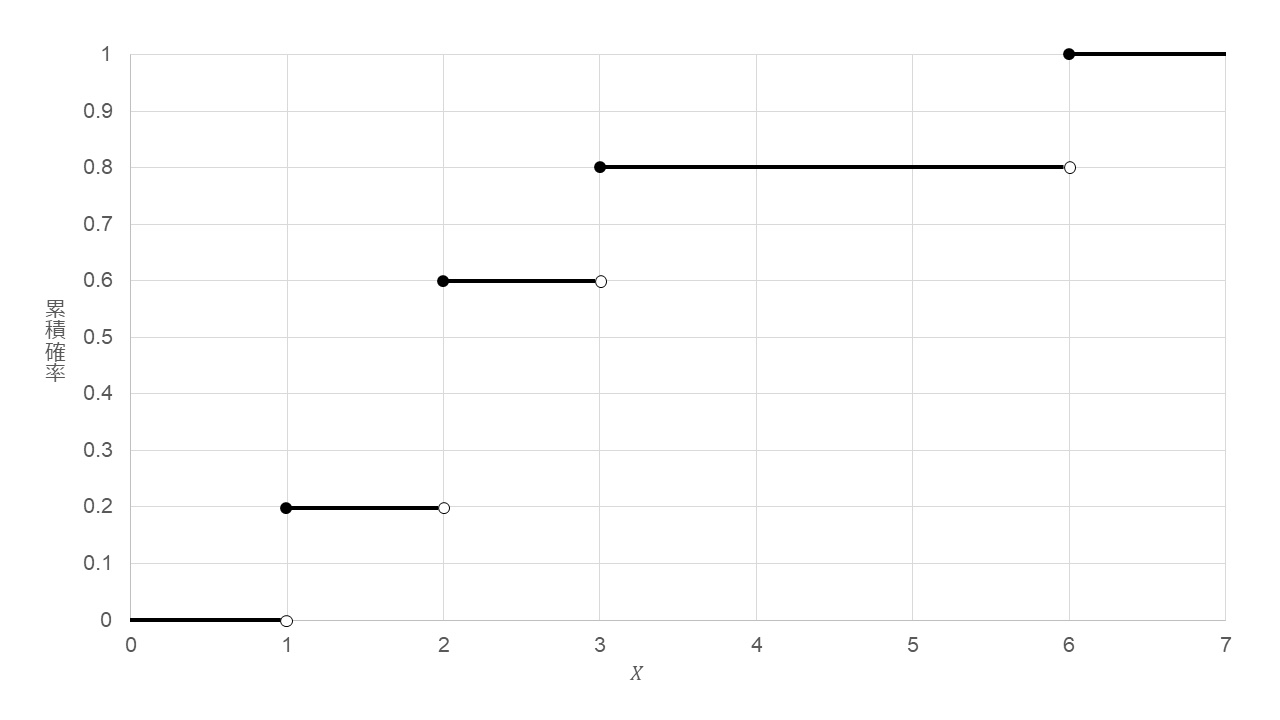
〔2〕標本平均と経験分布関数の関係
標本平均の値は、 \begin{align} \bar{X}&=1\times\frac{1}{5}+2\times\frac{2}{5}+3\times\frac{1}{5}+6\times\frac{1}{5}\\ &=1\times\frac{1}{5}+2\times \left(\frac{3}{5}-\frac{1}{5}\right)+3\times \left(\frac{4}{5}-\frac{3}{5}\right)+6\times \left(1-\frac{4}{5}\right) \end{align} この値は、経験分布関数において、以下に示す領域の面積を表している。 $\blacksquare$

〔3〕期待値と累積分布関数との関係
累積分布関数の定義式より、確率変数が非負の値のみを取る場合、 \begin{align} \int_{0}^{\infty} \left\{1-F \left(x\right)\right\}dx&=\int_{0}^{\infty} \left\{1-\int_{0}^{x}f \left(t\right)dt\right\}dx\\ &=\int_{0}^{\infty} \left\{\int_{0}^{\infty}f \left(t\right)dt-\int_{0}^{x}f \left(t\right)dt\right\}dx\\ &=\int_{0}^{\infty} \left(\int_{x}^{\infty}f \left(t\right)dt\right)dx \end{align} この計算において、$x,t$ の定義域は、 \begin{gather} 0 \le x \left( \le \infty\right)\\ x \le t \left( \le \infty\right) \end{gather} したがって、積分領域は、 \begin{gather} D= \left\{ \left(x,t\right)\middle|\ 0 \le x \le t,\ t\colon0 \le t \left( \le \infty\right)\right\} \end{gather} 本問の確率密度関数は、可積分な連続関数、かつ非負な連続関数であることから、積分の順序を入れ替えて、 \begin{align} \int_{0}^{\infty} \left\{1-F \left(x\right)\right\}dx&=\int_{0}^{\infty} \left(\int_{0}^{t}f \left(t\right)dx\right)dt\\ &=\int_{0}^{\infty}f \left(t\right) \left(\int_{0}^{t}dx\right)dt\\ &=\int_{0}^{\infty}{ \left[x \cdot f \left(t\right)\right]_0^tdt}\\ &=\int_{0}^{\infty}{t \cdot f \left(t\right)dt}\\ &=E \left(X\right) \end{align} $\blacksquare$
〔4〕指数分布とガンマ分布の混合分布
与式を計算すると、 \begin{align} f \left(x\right)&=\int_{0}^{\infty}{\lambda e^{-\lambda x} \cdot \frac{\beta^\alpha}{\Gamma \left(\alpha\right)}\lambda^{\alpha-1}e^{-\beta\lambda}d\lambda}\\ &=\frac{\beta^\alpha}{\Gamma \left(\alpha\right)}\int_{0}^{\infty}{\lambda^{ \left(\alpha+1\right)-1} \cdot e^{- \left(\beta+x\right)\lambda}d\lambda} \end{align} ガンマ関数の公式 \begin{align} \frac{\Gamma \left(a\right)}{b^a}=\int_{0}^{\infty}{\lambda^{a-1} \cdot e^{-b\lambda}d\lambda} \end{align} より、 $a=\alpha+1,b= \left(\beta+x\right)$ とし、与えられたガンマ関数の性質 $\Gamma \left(\alpha+1\right)=\alpha\Gamma \left(\alpha\right)$ を用いると、 \begin{align} f \left(x\right)&=\int_{0}^{\infty}{\lambda e^{-\lambda x} \cdot \frac{\beta^\alpha}{\Gamma \left(\alpha\right)}\lambda^{\alpha-1}e^{-\beta\lambda}d\lambda}\\ &=\frac{\beta^\alpha}{\Gamma \left(\alpha\right)} \cdot \frac{\Gamma \left(\alpha+1\right)}{ \left(\beta+x\right)^{\alpha+1}}\\ &=\frac{\alpha\beta^\alpha}{ \left(\beta+x\right)^{\alpha+1}} \end{align} $\blacksquare$
〔5〕混合分布の期待値
〔4〕で求めた混合分布の累積分布関数は、 \begin{align} F \left(x\right)&=\int_{0}^{x}{\frac{\alpha\beta^\alpha}{ \left(\beta+t\right)^{\alpha+1}}dt}\\ &=\alpha\beta^\alpha \left[-\frac{1}{\alpha} \cdot \frac{1}{ \left(\beta+x\right)^\alpha}\right]_0^x\\ &=\alpha\beta^\alpha \left(-\frac{1}{\alpha \left(\beta+x\right)^\alpha}+\frac{1}{\alpha\beta^\alpha}\right)\\ &=1- \left(\frac{\beta}{\beta+x}\right)^\alpha \end{align} 〔3〕の結果より、 \begin{align} E \left(X\right)&=\int_{0}^{\infty}{1- \left\{1- \left(\frac{\beta}{\beta+x}\right)^\alpha\right\}dx}\\ &=\int_{0}^{\infty}{ \left(\frac{\beta}{\beta+x}\right)^\alpha d x}\\ &=\beta^\alpha \left[-\frac{1}{\alpha-1} \cdot \frac{1}{ \left(\beta+x\right)^{\alpha-1}}\right]_0^\infty\\ &=\frac{\beta^\alpha}{\alpha-1} \left(\frac{1}{\beta^{\alpha-1}}-\lim_{x\rightarrow\infty}{\frac{1}{ \left(\beta+x\right)^{\alpha-1}}}\right) \end{align} ここで、まず \begin{gather} \alpha-1 \neq 0\\ \alpha \neq 1 \end{gather} また、$0 \lt \alpha \lt 1$ のとき、 \begin{align} \lim_{x\rightarrow\infty}{\frac{1}{ \left(\beta+x\right)^{\alpha-1}}} \end{align} が発散してしまうため、期待値が存在する範囲は、 \begin{align} 1 \lt \alpha \end{align} このとき、期待値は、 \begin{align} E \left(X\right)&=\frac{\beta^\alpha}{\alpha-1} \cdot \frac{1}{\beta^{\alpha-1}}\\ &=\frac{\beta}{\alpha-1} \end{align} $\blacksquare$



0 件のコメント:
コメントを投稿