統計検定 1級 2024年 医薬生物学 問2 治療効果の推定量の比較

本稿には、2024年に実施された統計検定1級『医薬生物学』 問2の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。

• 統計検定の問題の使用に関する規約により禁止されているため、問題文は掲載することができません。公式サイトで公開されているものなどをご参照ください。
• この答案は、あくまでも筆者が自作したものであり、公式なものではありません。正式な答案については、公式問題集をご参照ください。
• 計算ミスや誤字・脱字などがありましたら、コメントなどでご指摘いただければ大変助かります。
• スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。

 

〔1〕治療効果の推定量の分散①

問題文の条件より、 \begin{gather} E \left(X_{Ti}\right)=\mu_T^X, \quad E \left(Y_{Ti}\right)=\mu_T^Y, \quad E \left(X_{Ci}\right)=\mu_C^X, \quad E \left(Y_{Ci}\right)=\mu_C^Y\\ V \left(X_{Ti}\right)=V \left(Y_{Ti}\right)=V \left(X_{Ci}\right)=V \left(Y_{Ci}\right)=\sigma^2\\ \mathrm{Cov} \left(X_{Ti},Y_{Ti}\right)=\mathrm{Cov} \left(X_{Ci},Y_{Ci}\right)=\sigma^2\rho \end{gather} 被験者間のデータは互いに独立なので、 \begin{gather} \mathrm{Cov} \left(X_{Ti},X_{Ci}\right)=\mathrm{Cov} \left(X_{Ti},Y_{Ci}\right)=\mathrm{Cov} \left(Y_{Ti},X_{Ci}\right)=\mathrm{Cov} \left(Y_{Ti},Y_{Ci}\right)=0 \end{gather} 標本平均の期待値と分散の公式より、 \begin{gather} V \left({\bar{X}}_T\right)=V \left({\bar{Y}}_T\right)=V \left({\bar{X}}_C\right)=V \left({\bar{Y}}_C\right)=\frac{\sigma^2}{n} \end{gather}

標本平均どうしの共分散について、共分散の性質より、 \begin{align} \mathrm{Cov} \left(\bar{X},\bar{Y}\right)&=\mathrm{Cov} \left(\frac{1}{n}\sum_{i=0}^{n}X_i,\frac{1}{n}\sum_{i=0}^{n}Y_i\right)\\ &=\frac{1}{n} \cdot \frac{1}{n} \cdot \mathrm{Cov} \left(\sum_{i=0}^{n}X_i,\sum_{i=0}^{n}Y_i\right)\\ &=\frac{1}{n^2}\mathrm{Cov} \left(\sum_{i=0}^{n}X_i,\sum_{i=0}^{n}Y_i\right) \end{align} ここで、共分散には分配法則のようなものが成り立つことから、 \begin{align} \mathrm{Cov} \left(\bar{X},\bar{Y}\right)&=\frac{1}{n^2}\mathrm{Cov} \left\{ \left(X_1+X_2+ \cdots X_n\right), \left(Y_1+Y_2+ \cdots Y_n\right)\right\}\\ &=\frac{1}{n^2} \left\{\sum_{i=0}^{n}{\mathrm{Cov} \left(X_i,Y_i\right)}+\sum_{i=1}^{n}\sum_{j \neq i}{\mathrm{Cov} \left(X_i,Y_j\right)}\right\}\\ &=\frac{1}{n^2} \left\{n \cdot \mathrm{Cov} \left(X_i,Y_i\right)+0\right\}\\ &=\frac{\sigma^2\rho}{n} \end{align} これと同様に考え方から、 \begin{gather} \mathrm{Cov} \left({\bar{X}}_T,{\bar{Y}}_T\right)=\mathrm{Cov} \left({\bar{X}}_C,{\bar{Y}}_C\right)=\frac{\sigma^2\rho}{n}\\ \mathrm{Cov} \left({\bar{X}}_T,{\bar{X}}_C\right)=\mathrm{Cov} \left({\bar{X}}_T,{\bar{Y}}_C\right)=\mathrm{Cov} \left({\bar{Y}}_T,{\bar{X}}_C\right)=\mathrm{Cov} \left({\bar{Y}}_T,{\bar{Y}}_C\right)=0 \end{gather}

治療効果の推定量 ${\hat{\delta}}_d$ の分散は、和の分散の一般公式より、 \begin{align} V \left({\hat{\delta}}_d\right)&=V \left({\bar{Y}}_T-{\bar{Y}}_C\right)\\ &=V \left({\bar{Y}}_T\right)+V \left({\bar{Y}}_C\right)-2\mathrm{Cov} \left({\bar{Y}}_T,{\bar{Y}}_C\right)\\ &=\frac{\sigma^2}{n}+\frac{\sigma^2}{n}-0\\ &=\frac{2\sigma^2}{n} \end{align} $\blacksquare$

 

〔2〕治療効果の推定量の分散②

治療効果の推定量 ${\hat{\delta}}_c$ の分散は、和の分散の一般公式より、$0$ になるものの記載を省略すると、 \begin{align} V \left({\hat{\delta}}_c\right)&=V \left({\bar{Y}}_T-{\bar{X}}_T-{\bar{Y}}_C+{\bar{X}}_C\right)\\ &=V \left({\bar{Y}}_T\right)+V \left({\bar{X}}_T\right)+V \left({\bar{Y}}_C\right)+V \left({\bar{X}}_C\right)-2\mathrm{Cov} \left({\bar{Y}}_T,{\bar{X}}_T\right)-2\mathrm{Cov} \left({\bar{Y}}_C,{\bar{X}}_C\right)\\ &=\frac{\sigma^2}{n}\times4-\frac{2\sigma^2\rho}{n}\times2\\ &=\frac{4\sigma^2 \left(1-\rho\right)}{n} \end{align} $\blacksquare$

 

〔3〕回帰モデル

〔3-1〕最小二乗法によるパラメータの推定

まず、標本平均の定義式の変形より、 \begin{gather} \sum_{i=0}^{n}X_{Ti}=n{\bar{X}}_T, \quad \sum_{i=0}^{n}Y_{Ti}=n{\bar{Y}}_T\\ \sum_{i=0}^{n}X_{Ci}=n{\bar{X}}_T, \quad \sum_{i=0}^{n}Y_{Ci}=n{\bar{Y}}_T \end{gather}

試験治療群における誤差項は、 \begin{align} \varepsilon_{Ti}&=Y_{Ti}- \left(\alpha+\delta_a+\rho X_{Ti}\right)\\ \sum_{i}^{n}\varepsilon_{Ti}^2&=\sum_{i}^{n} \left\{Y_{Ti}- \left(\alpha+\delta_a+\rho X_{Ti}\right)\right\}^2 \end{align} 対照治療群における誤差項は、 \begin{align} \varepsilon_{Ci}&=Y_{Ci}- \left(\alpha+\rho X_{Ci}\right)\\ \sum_{i}^{n}\varepsilon_{Ci}^2&=\sum_{i}^{n} \left\{Y_{Ci}- \left(\alpha+\rho X_{Ci}\right)\right\}^2 \end{align} したがって、二乗誤差の総和は、 \begin{align} E=\sum_{i}^{n} \left\{Y_{Ti}- \left(\alpha+\delta_a+\rho X_{Ti}\right)\right\}^2+\sum_{i}^{n} \left\{Y_{Ci}- \left(\alpha+\rho X_{Ci}\right)\right\}^2 \end{align} 最小二乗法による推定を行うため、$E$ をパラメータ $\alpha$ で偏微分したものを $0$ として計算すると、 \begin{align} \frac{\partial E}{\partial\alpha}&=\sum_{i}^{n}2 \left\{Y_{Ti}- \left(\alpha+\delta_a+\rho X_{Ti}\right)\right\} \left(-1\right)+\sum_{i}^{n}2 \left\{Y_{Ci}- \left(\alpha+\rho X_{Ci}\right)\right\} \left(-1\right)\\ 0&=-2 \left[\sum_{i}^{n} \left\{Y_{Ti}- \left(\alpha+\delta_a+\rho X_{Ti}\right)\right\}+\sum_{i}^{n} \left\{Y_{Ci}- \left(\alpha+\rho X_{Ci}\right)\right\}\right]\\ &=\sum_{i}^{n} \left(Y_{Ti}-\rho X_{Ti}\right)-n \left(\alpha+\delta_a\right)+\sum_{i}^{n} \left(Y_{Ci}-\rho X_{Ci}\right)-n\alpha\\ &=\sum_{i}^{n}Y_{Ti}-\rho\sum_{i}^{n}X_{Ti}+\sum_{i}^{n}Y_{Ci}-\rho\sum_{i}^{n}X_{Ci}-2n\alpha-n\delta_a\\ &=n \left({\bar{Y}}_T-\rho{\bar{X}}_T+{\bar{Y}}_C-\rho{\bar{X}}_C-2\alpha-\delta_a\right) \end{align} したがって、 \begin{align} 2\alpha+\delta_a={\bar{Y}}_T-\rho{\bar{X}}_T+{\bar{Y}}_C-\rho{\bar{X}}_C\tag{1} \end{align} パラメータ $\delta_a$ についても同様に、 \begin{align} \frac{\partial E}{\partial\delta_a}&=\sum_{i}^{n}2 \left\{Y_{Ti}- \left(\alpha+\delta_a+\rho X_{Ti}\right)\right\}\\ 0&=2 \left[\sum_{i}^{n} \left(Y_{Ti}-\rho X_{Ti}\right)-n \left(\alpha+\delta_a\right)\right]\\ &=2n \left\{{\bar{Y}}_T-\rho{\bar{X}}_T- \left(\alpha+\delta_a\right)\right\}\\ &={\bar{Y}}_T-\rho{\bar{X}}_T- \left(\alpha+\delta_a\right) \end{align} したがって、 \begin{align} \alpha+\delta_a={\bar{Y}}_T-\rho{\bar{X}}_T\tag{2} \end{align} $2\times \left(2\right)- \left(1\right)$ より、 \begin{align} {\hat{\delta}}_a&=2{\bar{Y}}_T-2\rho{\bar{X}}_T- \left({\bar{Y}}_T-\rho{\bar{X}}_T+{\bar{Y}}_C-\rho{\bar{X}}_C\right)\\ &={\bar{Y}}_T-{\bar{Y}}_C-\rho{\bar{X}}_T+\rho{\bar{X}}_C \end{align} したがって、係数比較すると、 \begin{align} c_1=1, \quad c_2=-1, \quad c_3=-\rho, \quad c_4=\rho \end{align} $\blacksquare$

 

〔3-2〕治療効果の推定量の分散③

〔3-1〕の結果と和の分散の一般公式より、$0$ になる項の記載を省略すると、 \begin{align} V \left({\hat{\delta}}_a\right)&=V \left({\bar{Y}}_T-{\bar{Y}}_C-\rho{\bar{X}}_T+\rho{\bar{X}}_C\right)\\ &=V \left({\bar{Y}}_T\right)+V \left({\bar{Y}}_C\right)+\rho^2V \left({\bar{X}}_T\right)+\rho^2V \left({\bar{X}}_C\right)+2\mathrm{Cov} \left({\bar{Y}}_T,-\rho{\bar{X}}_T\right)+2\mathrm{Cov} \left(-{\bar{Y}}_C,\rho{\bar{X}}_C\right)\\ &=\frac{\sigma^2}{n}\times2+\frac{\sigma^2\rho^2}{n}\times2-2 \cdot \rho \cdot \frac{\sigma^2\rho}{n}\times2\\ &=\frac{2\sigma^2-2\sigma^2\rho^2}{n}\\ &=\frac{2\sigma^2 \left(1-\rho^2\right)}{n} \end{align} $\blacksquare$

 

〔4〕治療効果の推定量の期待値

標本平均の期待値の公式より、 \begin{align} E \left({\bar{Y}}_T\right)=\mu_T^Y \quad E \left({\bar{X}}_T\right)=\mu_T^X \quad E \left({\bar{Y}}_C\right)=\mu_C^Y \quad E \left({\bar{X}}_C\right)=\mu_C^X \end{align} それぞれの推定量の期待値を求めると、 \begin{align} E \left({\hat{\delta}}_d\right)&=E \left({\bar{Y}}_T-{\bar{Y}}_C\right)\\ &=E \left({\bar{Y}}_T\right)-E \left({\bar{Y}}_C\right)\\ &=\mu_T^Y-\mu_C^Y \end{align} \begin{align} E \left({\hat{\delta}}_c\right)&=E \left({\bar{Y}}_T-{\bar{X}}_T-{\bar{Y}}_C+{\bar{X}}_C\right)\\ &=E \left({\bar{Y}}_T\right)-E \left({\bar{X}}_T\right)- \left\{E \left({\bar{Y}}_C\right)-E \left({\bar{X}}_C\right)\right\}\\ &= \left(\mu_T^Y-\mu_C^Y\right)- \left(\mu_T^X-\mu_C^X\right) \end{align} \begin{align} E \left({\hat{\delta}}_a\right)&=E \left({\bar{Y}}_T-{\bar{Y}}_C-\rho{\bar{X}}_T+\rho{\bar{X}}_C\right)\\ &=E \left({\bar{Y}}_T\right)-E \left({\bar{Y}}_C\right)-\rho E \left({\bar{X}}_T\right)+\rho E \left({\bar{X}}_C\right)\\ &= \left(\mu_T^Y-\mu_C^Y\right)-\rho \left(\mu_T^X-\mu_C^X\right) \end{align} したがって、$E \left({\hat{\delta}}_d\right)=E \left({\hat{\delta}}_c\right)=E \left({\hat{\delta}}_a\right)$ となるための条件は、 \begin{align} \mu_T^X-\mu_C^X=0 \end{align} $\blacksquare$

 

〔5〕推定量の相対効率

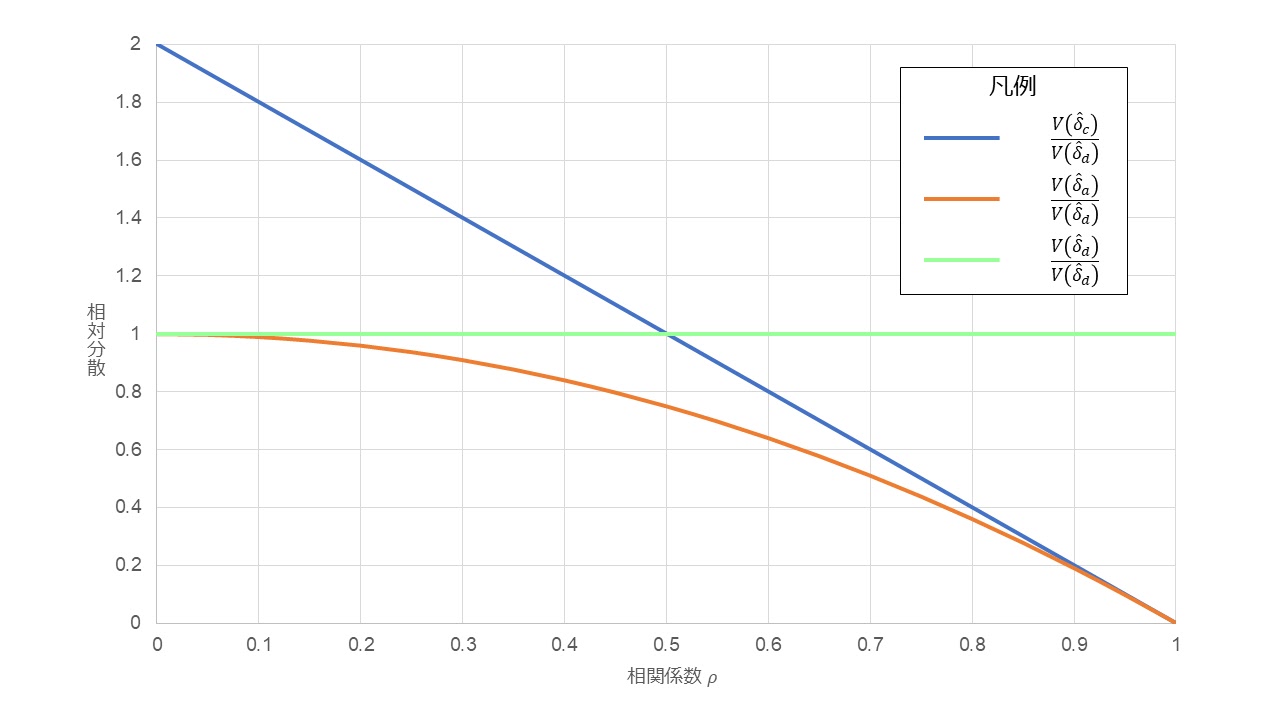
これまでの結果から、 \begin{align} \frac{V \left({\hat{\delta}}_c\right)}{V \left({\hat{\delta}}_d\right)}&=\frac{4\sigma^2 \left(1-\rho\right)}{n} \cdot \frac{n}{2\sigma^2}\\ &=2 \left(1-\rho\right) \end{align} \begin{align} \frac{V \left({\hat{\delta}}_a\right)}{V \left({\hat{\delta}}_d\right)}&=\frac{2\sigma^2 \left(1-\rho^2\right)}{n} \cdot \frac{n}{2\sigma^2}\\ &=1-\rho^2 \end{align}

これをグラフにすると、以下のようになる。 $\blacksquare$

 

関連記事

• 標本平均の期待値と分散
• 共分散の定義と基本性質
• 相関係数の定義と基本性質
• 確率変数の和（差）の分散の一般公式