統計検定 1級 2017年 統計数理 問2 連続一様分布の上限値の推定

本稿には、2017年に実施された統計検定1級『統計数理』 問2の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。

〔1〕連続一様分布の最尤推定量

本問において、確率変数 $X$ は \begin{align} \mathrm{U} \sim \left(0,\theta\right) \end{align} 尤度関数 $L \left(\theta\right)$ を求めると、 \begin{align} L \left(\theta\right)&=\prod_{i=1}^{n}\frac{1}{\theta}\\ &=\frac{1}{\theta^n} \end{align} 対数尤度関数 $l \left(\theta\right)=\log{L \left(\theta\right)}$ を求めると、 \begin{align} l \left(\theta\right)=-n\log{\theta} \end{align} ここで、この対数尤度関数は、$0 \lt \theta$ において単調減少な関数であり、論理的に、 \begin{align} X_{\mathrm{max}} \le \theta \end{align} という制約があるため、 実際には、 \begin{align} l \left(\theta\right)= \left\{\begin{matrix}0&\theta \lt X_{\mathrm{max}}\\-n\log{\theta}&X_{\mathrm{max}} \le \theta\\\end{matrix}\right. \end{align} したがって、対数尤度関数は、 \begin{align} \hat{\theta}=X_{\mathrm{max}} \end{align} において最大となるから、 最尤推定量の定義より、$\theta$ の最尤推定量は $\hat{\theta}=X_{\mathrm{max}}$ である。 $\blacksquare$

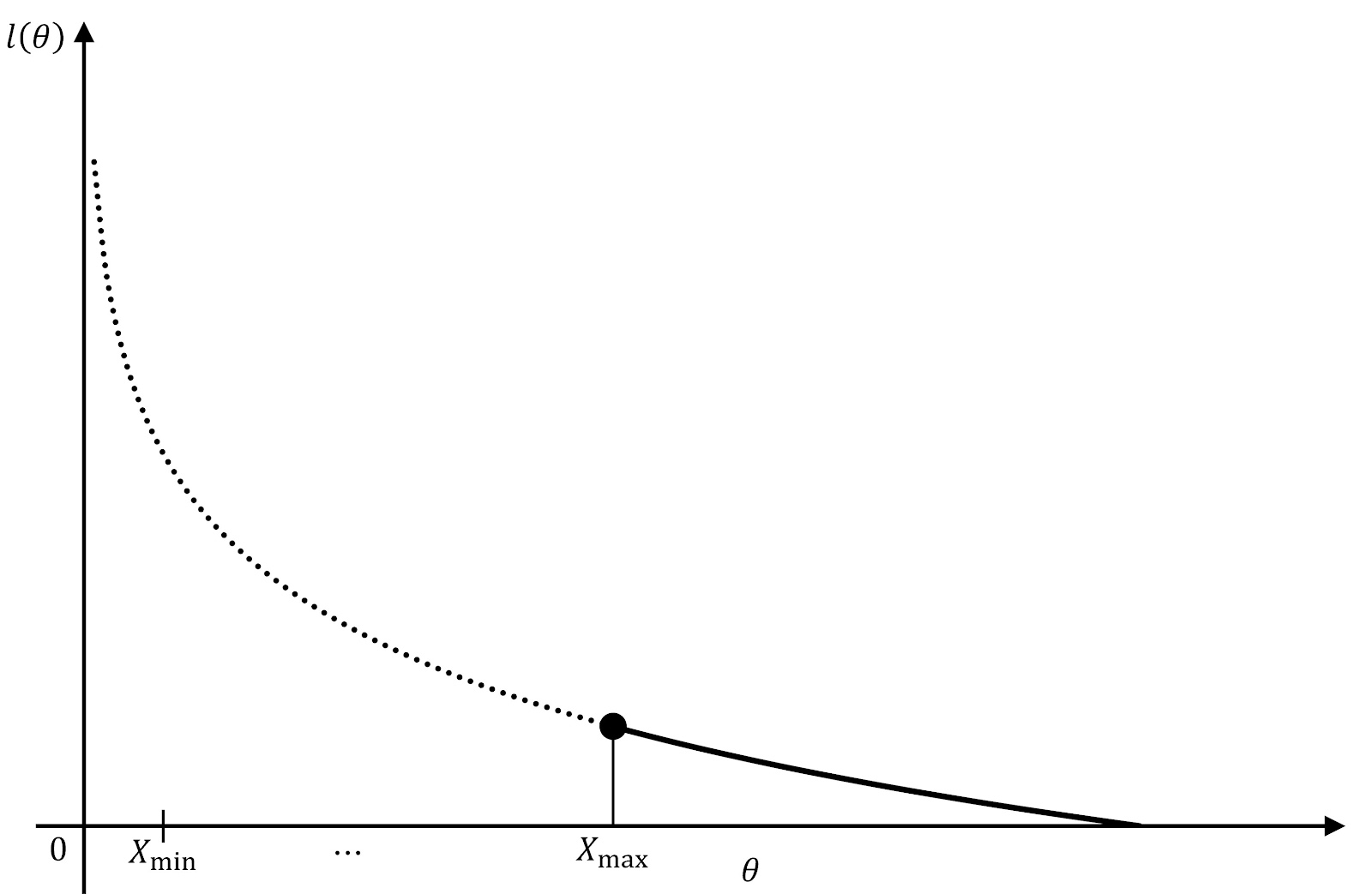
〔2〕連続一様分布の不偏推定量

期待値の定義式 $E \left(X\right)=\int_{-\infty}^{\infty}{x \cdot f \left(x\right)dx}$ より、この分布の期待値は、 \begin{align} E \left(X\right)&=\int_{0}^{\theta}{x \cdot \frac{1}{\theta}dx}\\ &=\frac{1}{\theta} \left[\frac{1}{2}x^2\right]_0^\theta\\ &=\frac{1}{\theta} \left(\frac{b^2}{2}-\frac{a^2}{2}\right)\\ &=\frac{1}{\theta} \cdot \frac{\theta^2}{2}\\ &=\frac{\theta}{2} \end{align} $\theta^\prime$ の期待値を取ると、 \begin{align} E \left(\theta^\prime\right)&=E \left(\frac{2}{n}\sum_{i=1}^{n}X_i\right)\\ &=\frac{2}{n}E \left(\sum_{i=1}^{n}X_i\right)\\ &=\frac{2}{n}\sum_{i=1}^{n}E \left(X_i\right)\\ &=\frac{2}{n} \cdot \frac{n\theta}{2}\\ &=\theta \end{align} よって、$E \left(\hat{\theta}\right)=\theta$ が成り立つので、$\theta^\prime$ は $\theta$ の不偏推定量である。 $\blacksquare$

〔3〕最大値の分布

（i）累積分布関数
累積分布関数の定義式 $F \left(x\right)=\int_{-\infty}^{x}f \left(t\right)dt$ より、
$0 \lt x \le \theta$ のとき \begin{align} F \left(x\right)&=\int_{0}^{x}{\frac{1}{\theta}dt}\\ &=\frac{1}{\theta}\int_{0}^{x}{1 \cdot d t}\\ &=\frac{1}{\theta} \left[t\right]_0^x\\ &=\frac{x}{\theta} \end{align}

（ii）最大値の分布
最大値が $x$ 以下となるとき、すべての $X_i$ が $x$ 以下となるので、 \begin{align} F_{\mathrm{max}} \left(x\right)=P \left(X_1 \le x,X_2 \le x, \cdots X_n \le x\right) \end{align} すべての確率変数は互いに独立であるため、この確率は、 \begin{align} F_{\mathrm{max}} \left(x\right)&=P \left(X_1 \le x\right) \cdot P \left(X_2 \le x\right) \cdot \cdots \cdot P \left(X_n \le x\right)\\ &=F \left(x\right) \cdot F \left(x\right) \cdot \cdots \cdot F \left(x\right)\\ &= \left\{F \left(x\right)\right\}^n\\ &=\frac{x^n}{\theta^n} \end{align} 累積分布関数と確率密度関数の関係 $f \left(x\right)=\frac{d}{dx}F \left(x\right)$ より、 \begin{align} f_{\mathrm{max}} \left(x\right)=\frac{nx^{n-1}}{\theta^n} \end{align}

（iii）$\theta^{\prime\prime}$ の期待値
期待値の定義式 $E \left(X\right)=\int_{-\infty}^{\infty}{x \cdot f \left(x\right)dx}$ より、 \begin{align} E \left(X_{\mathrm{max}}\right)&=\int_{0}^{\theta}{x \cdot \frac{nx^{n-1}}{\theta^n}dx}\\ &=\frac{n}{\theta^n}\int_{0}^{\theta}{x^n \cdot d x}\\ &=\frac{n}{\theta^n} \left[\frac{1}{n+1}x^{n+1}\right]_0^\theta\\ &=\frac{n}{\theta^n} \cdot \frac{1}{n+1}\theta^{n+1}\\ &=\frac{n}{n+1} \cdot \theta\\ \end{align} 期待値の性質 $E \left(aX\right)=aE \left(X\right)$ より、 \begin{align} E \left(\theta^{\prime\prime}\right)&=E \left(\frac{n+1}{n}X_{\mathrm{max}}\right)\\ &=\frac{n+1}{n}E \left(X_{\mathrm{max}}\right)\\ &=\frac{n+1}{n} \cdot \frac{n}{n+1} \cdot \theta\\ &=\theta \end{align} よって、$E \left(\hat{\theta}\right)=\theta$ が成り立つので、$\theta^{\prime\prime}$ は $\theta$ の不偏推定量である。 $\blacksquare$

〔4〕不偏推定量の相対効率

（i）$\theta^\prime$ の分散
2乗の期待値の定義式 $E \left(X^2\right)=\int_{-\infty}^{\infty}{x^2 \cdot f \left(x\right)dx}$ より、 \begin{align} E \left(X^2\right)&=\int_{0}^{\theta}x^2 \cdot \frac{1}{\theta}dx\\ &=\frac{1}{\theta} \left[\frac{1}{3}x^3\right]_0^\theta\\ &=\frac{\theta^2}{3} \end{align} 分散の公式 $V \left(X\right)=E \left(X^2\right)- \left\{E \left(X\right)\right\}^2$ より、 \begin{align} V \left(X\right)&=\frac{\theta^2}{3}-\frac{\theta^2}{4}\\ &=\frac{\theta^2}{12} \end{align} これを用いて、$\theta^\prime$ の分散を求めると、 \begin{align} V \left(\theta^\prime\right)&=V \left(\frac{2}{n}\sum_{i=1}^{n}X_i\right)\\ &=\frac{4}{n^2}\sum_{i=1}^{n}V \left(X_i\right)\\ &=\frac{4}{n^2} \cdot \frac{n\theta^2}{12}\\ &=\frac{\theta^2}{3n} \end{align}

（ii）$\theta^\prime$ の分散
2乗の期待値の定義式 $E \left(X^2\right)=\int_{-\infty}^{\infty}{x^2 \cdot f \left(x\right)dx}$ より、 \begin{align} E \left(X_{\mathrm{max}}^2\right)&=\int_{0}^{\theta}x^2 \cdot \frac{n}{\theta^n}x^{n-1}dx\\ &=\frac{n}{\theta^n} \left[\frac{1}{n+2}x^{n+2}\right]_0^\theta\\ &=\frac{n}{\theta^n} \cdot \frac{\theta^{n+2}}{n+2}\\ &=\frac{n}{n+2}\theta^2 \end{align} 分散の公式 $V \left(X\right)=E \left(X^2\right)- \left\{E \left(X\right)\right\}^2$ より、 \begin{align} V \left(X_{\mathrm{max}}\right)&=\frac{n}{n+2}\theta^2-\frac{n^2}{ \left(n+1\right)^2}\theta^2\\ &=\frac{n \left(n^2+2n+1\right)-n^2 \left(n+2\right)}{ \left(n+2\right) \left(n+1\right)^2}\theta^2\\ &=\frac{n^3+2n^2+n-n^3-2n^2}{ \left(n+2\right) \left(n+1\right)^2}\theta^2\\ &=\frac{n}{ \left(n+2\right) \left(n+1\right)^2}\theta^2 \end{align} これを用いて、$\theta^{\prime\prime}$ の分散を求めると、 \begin{align} V \left(\theta^{\prime\prime}\right)&=V \left(\frac{n+1}{n}X_{\mathrm{max}}\right)\\ &=\frac{ \left(n+1\right)^2}{n^2}V \left(X_{\mathrm{max}}\right)\\ &=\frac{ \left(n+1\right)^2}{n^2} \cdot \frac{n}{ \left(n+2\right) \left(n+1\right)^2}\theta^2\\ &=\frac{\theta^2}{n \left(n+2\right)} \end{align}

（iii）推定量の分散の大小関係
$n \left(n+2\right)$ と $3n$ の大小関係について、$1 \le n$ なので、 \begin{align} n \left(n+2\right)-3n&=n^2+2n-3n\\ &=n^2-n\\ &=n \left(n-1\right) \geq 0 \end{align} よって、 \begin{align} 3n \le n \left(n+2\right)\Leftrightarrow\frac{1}{3n} \geq \frac{1}{n \left(n+2\right)} \end{align} これより、$n=1$ のときは、 \begin{align} V \left(\theta^\prime\right)=V \left(\theta^{\prime\prime}\right) \end{align} $2 \le n$ のときは、 \begin{align} V \left(\theta^\prime\right) \gt V \left(\theta^{\prime\prime}\right) \end{align} すなわち、サンプルサイズが2以上であれば、$\theta^{\prime\prime}$ の方がより望ましい。 $\blacksquare$

関連記事

• 連続一様分布の期待値・分散
• 推定量の評価
• 最尤推定法とモーメント法
• 最大値・最小値の分布