本稿には、2015年に実施された統計検定1級『統計数理』 問2の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。
- 著作権の関係上、問題文は、掲載することができません。申し訳ありませんが、閲覧者のみなさまでご用意いただければ幸いです。
- この答案は、あくまでも筆者が自作したものであり、公式なものではありません。正式な答案については、公式問題集をご参照ください。
- 計算ミスや誤字・脱字などがありましたら、コメントなどでご指摘いただければ大変助かります。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
〔1〕有意確率の算出
正規分布の標本平均の従う分布は、 \begin{align} \bar{X} \sim \mathrm{N} \left(\mu,\frac{1}{n}\right) \end{align} これを標準化した値は、 \begin{align} \sqrt n \left(\bar{X}-\mu\right)=Z_1 \sim \mathrm{N} \left(0,1\right) \end{align} 帰無仮説 $\mu=0$ において、$n=10,\bar{x}=0.3,\bar{x}=0.6$ のときの有意確率は、 \begin{gather} P \left(0.3 \cdot \sqrt{10} \le Z_0\right)\cong P \left(0.95 \le Z_0\right)=0.1711\\ P \left(0.6 \cdot \sqrt{10} \le Z_0\right)\cong P \left(1.90 \le Z_0\right)=0.0287 \end{gather} グラフの概形を描くと以下のようになる。 $\blacksquare$
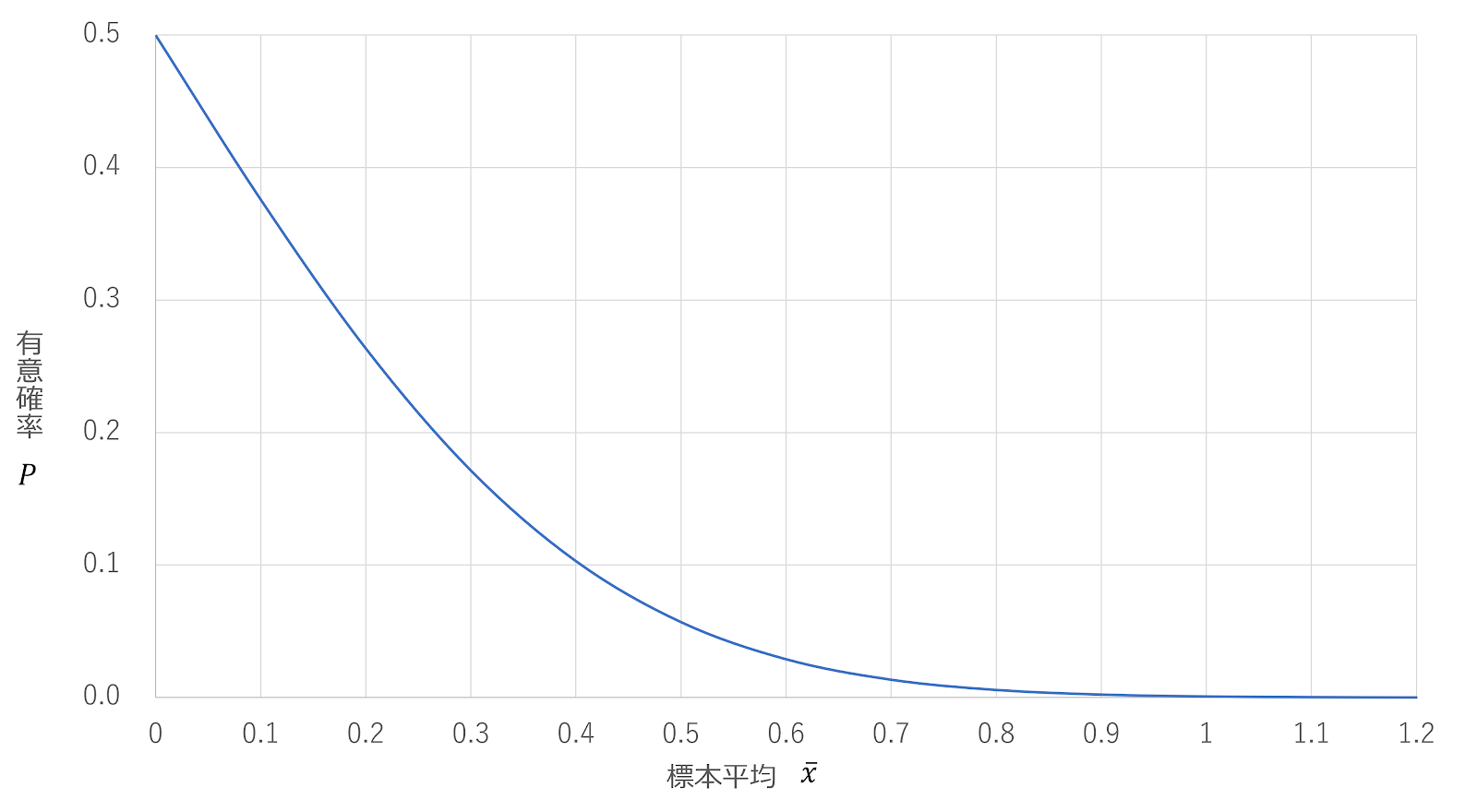
〔2〕分布関数による有意確率の表現
〔1〕と同様に考えると、 \begin{align} P&=P \left(\sqrt n\bar{x} \le Z_0\right)\\ &=1-P \left(Z_0 \le \sqrt n\bar{x}\right)\\ &=1-\Phi \left(\sqrt n\bar{x}\right) \end{align} $P$-値が $\alpha$ より小さくなるとき、 \begin{gather} P \left(\sqrt n\bar{X} \le Z_0\right) \lt \alpha\Leftrightarrow z_\alpha \lt \sqrt n\bar{X}\\ \frac{1}{\sqrt n}z_\alpha \lt \bar{X} \end{gather} したがって、$P$-値が $\alpha$ より小さくなることと、$\bar{x}$ が棄却域に落ちることは同等である。 $\blacksquare$
〔3〕検出力の算出
検出力の定義式より、 \begin{align} 1-\beta&=P \left(z_\alpha \le \sqrt n\bar{X}\middle|0 \lt \mu\right)\\ &=P \left\{z_\alpha-\mu\sqrt n \le \sqrt n \left(\bar{X}-\mu\right)\middle|0 \lt \mu\right\}\\ &=P \left(z_\alpha-\mu\sqrt n \le Z_1\middle|0 \lt \mu\right) \end{align} $\alpha=0.05\Leftrightarrow z_\alpha=1.64$ のとき \begin{align} 1-\beta=P \left(1.64-\mu\sqrt n \le Z_1\middle|0 \lt \mu\right) \end{align} (i)$n=9,\mu=0.4$ のとき \begin{align} 1-\beta&=P \left(1.64-0.4\sqrt9 \le Z_1\right)\\ &=P \left(0.44 \le Z_1\right)\\ &=0.3300 \end{align} (ii)$n=9,\mu=0.8$ のとき \begin{align} 1-\beta&=P \left(1.64-0.8\sqrt9 \le Z_1\right)\\ &=P \left(-0.76 \le Z_1\right)\\ &=0.7764 \end{align} (iii)$n=16,\mu=0.4$ のとき \begin{align} 1-\beta&=P \left(1.64-0.4\sqrt{16} \le Z_1\right)\\ &=P \left(0.04 \le Z_1\right)\\ &=0.4840 \end{align} (ii)$n=16,\mu=0.8$ のとき \begin{align} 1-\beta&=P \left(1.64-0.8\sqrt{16} \le Z_1\right)\\ &=P \left(-1.56 \le Z_1\right)\\ &=0.9406 \end{align} グラフの概形を描くと以下のようになる。 $\blacksquare$
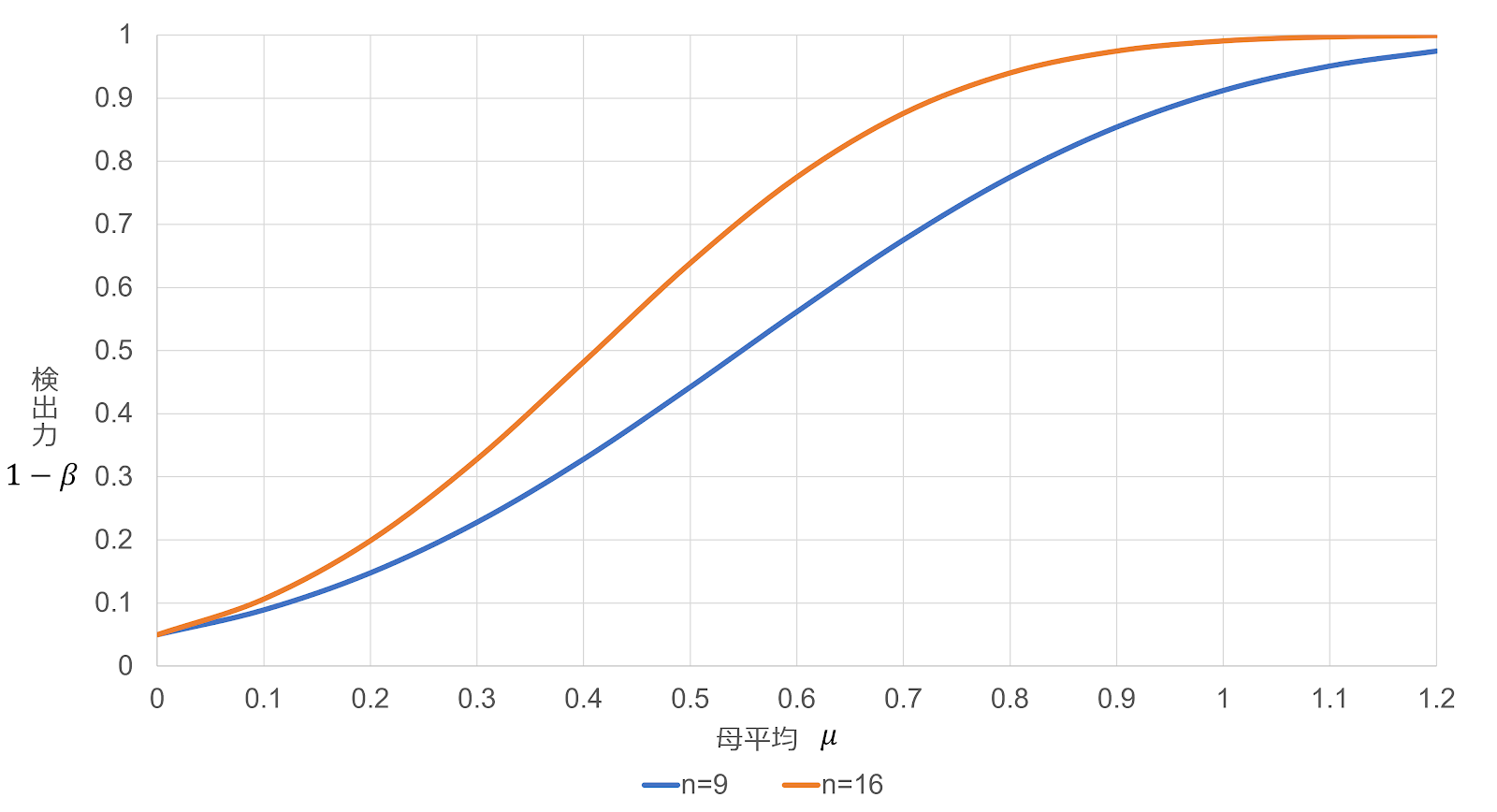
〔4〕サンプルサイズの設計
〔3〕の結果より、$\mu=0.5,1-\beta \geq 0.8$ のとき、 \begin{gather} P \left(1.64-0.5\sqrt n \le Z_1\right) \le 0.8\\ 1.64-0.5\sqrt n \le Z_{0.8}\\ 1.64-0.5\sqrt n \le -0.84\\ 1.64+0.84 \le 0.5\sqrt n\\ 4.96 \le \sqrt n\\ 24.6 \le n \end{gather} これを満たす最小の整数を考えると、サンプルサイズは、 \begin{align} 25 \le n \end{align} $\blacksquare$
〔5〕一様最強力検定の導出
本問の場合、ネイマン・ピアソンの基本定理の内容は、単純仮説による検定問題 \begin{align} \begin{matrix}H_0:\mu=0&H_1:\mu=\mu_1 \left( \gt 0\right)\\\end{matrix} \end{align} を考えるにあたり、 尤度比を標本平均 $\bar{x}$ の関数 \begin{align} \lambda \left(x\right)=\frac{f_1 \left(\boldsymbol{x}\middle|\mu=\mu_1\right)}{f_0 \left(\boldsymbol{x}\middle|\mu=0\right)}=g \left(\bar{x}\right) \end{align} として、 「以下の棄却域と検定関数をもつ検定が有意水準を $\alpha$ とする最強力検定である」というものである。 \begin{align} \varphi \left(\theta;\boldsymbol{x}\right)= \left\{\begin{matrix}\lambda \left(x\right) \lt k&\mathrm{0:Accept\ }H_0\\\lambda \left(x\right) \gt k&\mathrm{1:Reject\ }H_0\\\end{matrix}\right.\\ \Leftrightarrow\varphi \left(\theta;\boldsymbol{x}\right)= \left\{\begin{matrix}\bar{x} \lt k^\prime&\mathrm{0:Accept\ }H_0\\\bar{x} \gt k^\prime&\mathrm{1:Reject\ }H_0\\\end{matrix}\right. \end{align} ただし、定数 $k^\prime$ は、$0 \lt k^\prime$ を満たし、 \begin{align} P \left\{\bar{x}\in R\middle|\mu=0\right\}=\alpha \end{align} 本問の場合、棄却域を \begin{align} \frac{z_\alpha}{\sqrt n} \lt \bar{x} \end{align} とすることで、 第1種の過誤の確率が $\alpha$ に制御できる。この棄却域は、$\mu_1 \left( \gt 0\right)$ の値に依存しないので、一様最強力検定である。 $\blacksquare$



0 件のコメント:
コメントを投稿