本稿には、2013年に実施された統計検定1級『統計数理』 問1の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。
- 著作権の関係上、問題文は、掲載することができません。申し訳ありませんが、閲覧者のみなさまでご用意いただければ幸いです。
- この答案は、あくまでも筆者が自作したものであり、公式なものではありません。正式な答案については、公式問題集をご参照ください。
- 計算ミスや誤字・脱字などがありましたら、コメントなどでご指摘いただければ大変助かります。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
〔1〕期待値・標準偏差・相関係数の算出
題意において、 \begin{gather} Y=1-X\\ 0 \lt X \le \frac{1}{2}\\ \frac{1}{2} \le Y \lt 1\\ \end{gather} であり、 確率変数 $X$ と $Y$ は、それぞれ、 \begin{align} X \sim \mathrm{U} \left(0,\frac{1}{2}\right) \quad Y \sim \mathrm{U} \left(\frac{1}{2},1\right) \end{align} 確率変数 $X$ の累積分布関数と確率密度関数は、 \begin{gather} G \left(x\right)= \left\{\begin{matrix}0&x \le 0\\2x&0 \lt x \le \frac{1}{2}\\1&\frac{1}{2} \lt x\\\end{matrix}\right.\\ g \left(x\right)= \left\{\begin{matrix}2&0 \lt x \le \frac{1}{2}\\0&\mathrm{other}\\\end{matrix}\right. \end{gather}
(i)期待値
(i-x)期待値の定義式 $E \left(X\right)=\int_{-\infty}^{\infty}{x \cdot f \left(x\right)dx}$ より、
\begin{align}
E \left(X\right)&=\int_{0}^{\frac{1}{2}}2xdx\\
&= \left[x^2\right]_0^{\frac{1}{2}}\\
&=\frac{1}{4}
\end{align}
(i-y)期待値の性質 $E \left(aX+b\right)=aE \left(X\right)+b$ より、
\begin{align}
E \left(Y\right)&=E \left(1-X\right)\\
&=1-\frac{1}{4}\\
&=\frac{3}{4}
\end{align}
(ii)標準偏差
(ii-x)2乗の期待値の定義式 $E \left(X^2\right)=\int_{-\infty}^{\infty}{x^2 \cdot f \left(x\right)dx}$ より、
\begin{align}
E \left(X^2\right)&=\int_{0}^{\frac{1}{2}}{2x^2dx}\\
&= \left[\frac{2}{3}x^3\right]_0^{\frac{1}{2}}\\
&=\frac{2}{3} \left(\frac{1}{8}-0\right)\\
&=\frac{1}{12}
\end{align}
分散の公式 $V \left(X\right)=E \left(X^2\right)- \left\{E \left(X\right)\right\}^2$ より、
\begin{align}
V \left(X\right)&=\frac{1}{12}-\frac{1}{16}\\
&=\frac{1}{48}
\end{align}
したがって、標準偏差は、
\begin{align}
\sigma_X&=\frac{1}{4\sqrt3}
\end{align}
(ii-y)
\begin{align}
E \left(Y^2\right)&=E \left\{ \left(1-X\right)^2\right\}\\
&=E \left(1-2X+X^2\right)\\
&=1-2E \left(X\right)+E \left(X^2\right)\\
&=1-2 \cdot \frac{1}{4}+\frac{1}{12}\\
&=\frac{7}{12}
\end{align}
分散の公式 $V \left(X\right)=E \left(X^2\right)- \left\{E \left(X\right)\right\}^2$ より、
\begin{align}
V \left(Y\right)&=\frac{7}{12}-\frac{9}{16}\\
&=\frac{1}{48}
\end{align}
したがって、標準偏差は、
\begin{align}
\sigma_Y&=\frac{1}{4\sqrt3}
\end{align}
(iii)相関係数
共分散の公式 $\mathrm{Cov} \left(X,Y\right)=E \left(XY\right)-E \left(X\right)E \left(Y\right)$ より、
\begin{align}
\mathrm{Cov} \left(X,Y\right)&=E \left\{X \left(1-X\right)\right\}-E \left(X\right)E \left(1-X\right)\\
&=E \left(X-X^2\right)-E \left(X\right) \left\{1-E \left(X\right)\right\}\\
&=E \left(X\right)-E \left(X^2\right)-E \left(X\right)+ \left\{E \left(X\right)\right\}^2\\
&=-V \left(X\right)
\end{align}
相関係数の定義式 $\rho_{XY}=\frac{\mathrm{Cov} \left(X,Y\right)}{\sigma_X \cdot \sigma_Y}$ より、
\begin{align}
\rho_{XY}&=-\frac{V \left(X\right)}{\sqrt{V \left(X\right)} \cdot \sqrt{V \left(Y\right)}}\\
&=\frac{V \left(X\right)}{\sqrt{V \left(X\right)} \cdot \sqrt{V \left(X\right)}}\\
&=-1
\end{align}
$\blacksquare$
〔2〕比の分布
題意において、 \begin{gather} W=\frac{X}{1-X}\\ 0 \lt W \le 1\\ \end{gather} 累積分布関数の定義式 $F \left(w\right)=P \left(W \le w\right)$ より、 \begin{align} F \left(w\right)&=P \left(\frac{X}{1-X} \le w\right)\\ &=P \left(X \le \frac{w}{1+w}\right)\\ &=G \left(\frac{w}{1+w}\right) \end{align} したがって、 \begin{gather} F \left(w\right)= \left\{\begin{matrix}0&w \le 0\\\frac{2w}{1+w}&0 \lt w \le 1\\1&1 \lt w\\\end{matrix}\right. \end{gather} 累積分布関数と確率密度関数の関係 $f \left(w\right)=\frac{d}{dx}F \left(w\right)$ より、 \begin{align} f \left(w\right)&=\frac{2 \left(1+w\right)-2w}{ \left(1+w\right)^2}\\ &=\frac{2}{ \left(1+w\right)^2} \end{align} したがって、 \begin{gather} f \left(w\right)= \left\{\begin{matrix}\frac{2}{ \left(1+w\right)^2}&0 \lt w \le 1\\0&\mathrm{other}\\\end{matrix}\right. \end{gather} また、それぞれのグラフの概形を描くと以下のようになる。 $\blacksquare$
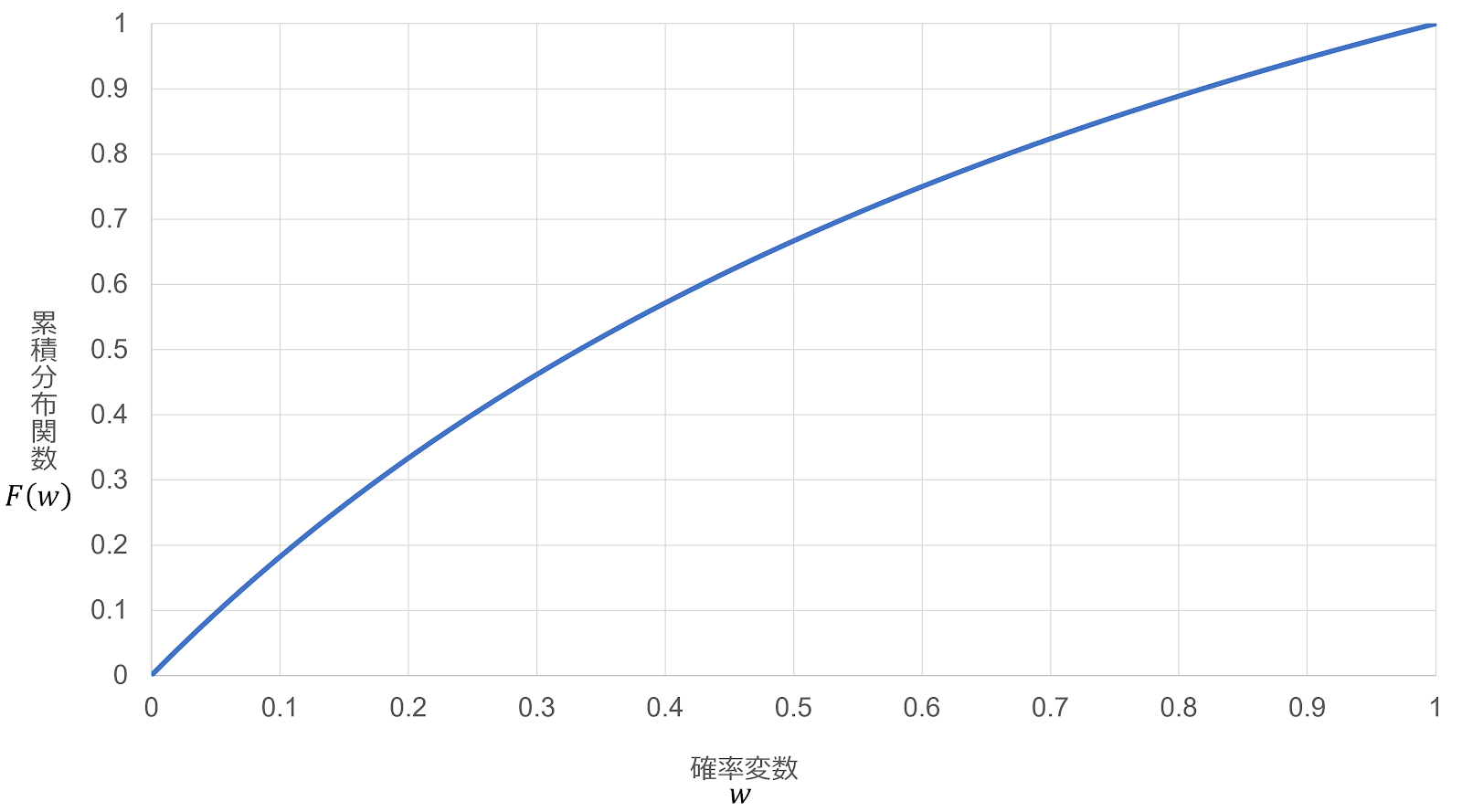
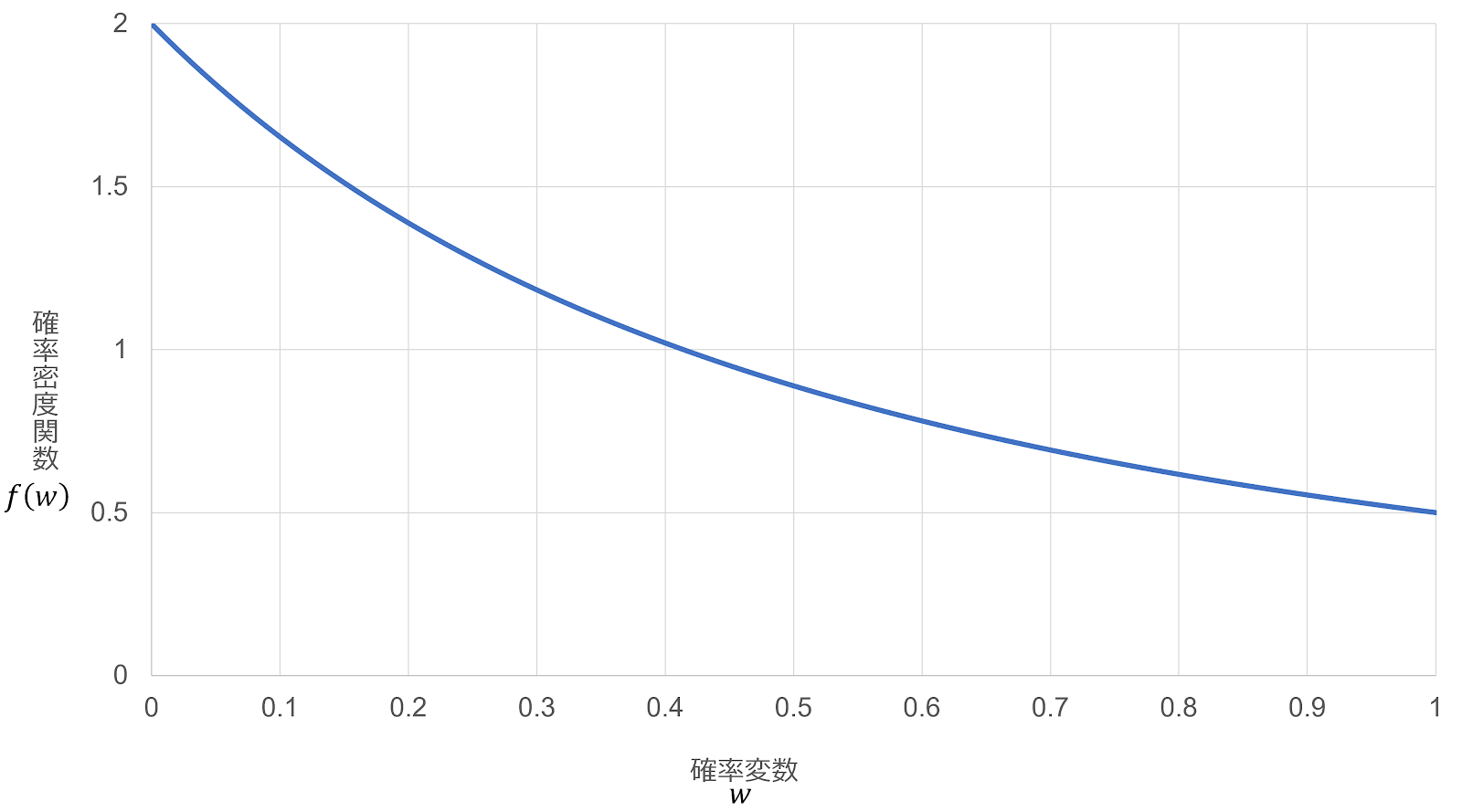
〔3〕比の期待値・中央値
中央値の定義 $F \left(w\right)=\frac{1}{2}$ より、 \begin{gather} \frac{2w}{1+w}=\frac{1}{2}\\ 4w=1+w\\ 3w=1\\ w=\frac{1}{3} \end{gather} 期待値の定義式 $E \left(X\right)=\int_{-\infty}^{\infty}{x \cdot f \left(x\right)dx}$ より、 \begin{align} E \left(W\right)&=\int_{0}^{1}{w \cdot f \left(w\right)dw}\\ &=\int_{0}^{1}{\frac{2w}{ \left(1+w\right)^2}dw} \end{align} ここで、部分分数分解すると、 \begin{align} \frac{2w}{ \left(1+w\right)^2}&=\frac{2 \left(1+w\right)-2}{ \left(1+w\right)^2}\\ &=\frac{2}{1+w}-\frac{2}{ \left(1+w\right)^2} \end{align} したがって、 \begin{align} E \left(W\right)=\int_{0}^{1}{\frac{2}{1+w}dw}-\int_{0}^{1}{\frac{2}{ \left(1+w\right)^2}dw} \end{align} ここで、$f \left(w\right)=\frac{2}{ \left(1+w\right)^2}$ なので、確率密度関数の性質から、 \begin{align} \int_{0}^{1}{\frac{2}{ \left(1+w\right)^2}dw}=1 \end{align} よって、 \begin{align} E \left(W\right)&=\int_{0}^{1}{\frac{2}{1+w}dw}-1\\ &=2 \left[\log{ \left(1+w\right)}\right]_0^1-1\\ &=2 \left(\log{2}-\log{1}\right)-1\\ &=2\log{2}-1 \end{align} $\blacksquare$



0 件のコメント:
コメントを投稿