統計検定 1級 2012年 統計数理 問1 連続一様分布の順序統計量の分布

本稿には、2012年に実施された統計検定1級『統計数理』 問1の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。

〔1〕確率積分変換

累積分布関数の定義から、$P \left(Z \lt 0\right)=P \left(1 \lt Z\right)=0$ であり、$Z$ の定義域は、$0 \le Z \le 1$ である。

ここで、$U$ の累積分布関数を $G \left(u\right)$ とすると、 \begin{align} G \left(u\right)&=P \left(U \le u\right)\\ &=P \left\{F \left(Z\right) \le u\right\}\\ \end{align} また、$F \left(z\right)$\ は狭義単調増加関数なので、逆関数 $Z=F^{-1} \left(u\right)$ が存在することから \begin{align} G \left(u\right)&=P \left\{Z \le F^{-1} \left(u\right)\right\}\\ &=F \left\{F^{-1} \left(u\right)\right\}\\ &=u \end{align} これは、一様分布 \begin{align} \mathrm{U} \left(0,1\right) \end{align} の累積分布関数であるから、 累積分布関数の一意性により、 \begin{align} Z \sim \mathrm{U} \left(0,1\right) \end{align} $\blacksquare$

〔2〕順序統計量の分布

まず、確率変数 $X_j$ の累積分布関数と確率密度関数をそれぞれ \begin{gather} G_j \left(x\right) \quad g_j \left(x\right)\\ 0 \le x \le 1 \end{gather} とする。

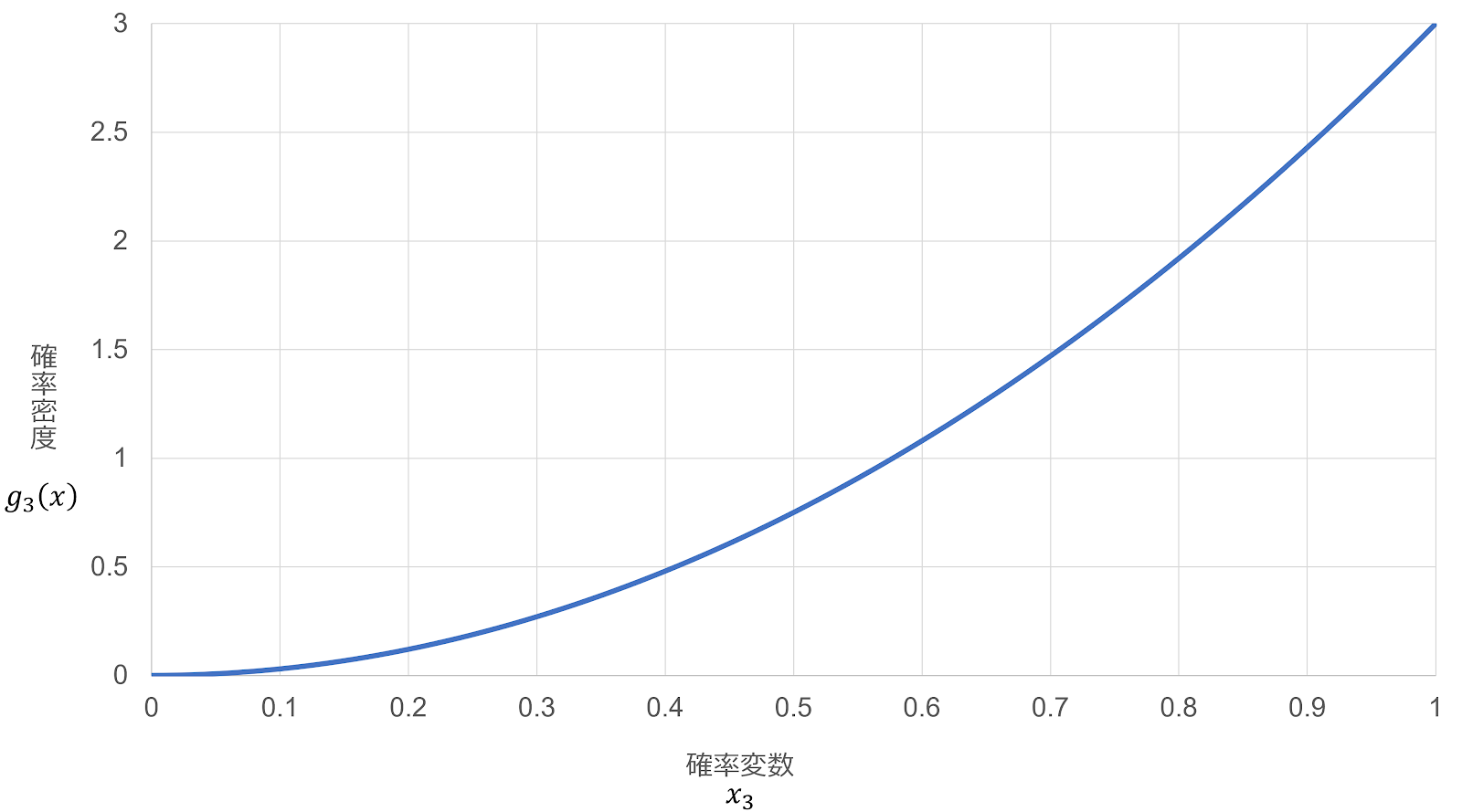
（i）最大値 $X_3$ の分布
最大値が $x$ 以下となるとき、すべての $X_j$ が $x$ 以下となるので、 \begin{align} G_3 \left(x\right)=P \left(X_1 \le x,X_2 \le x,X_3 \le x\right) \end{align} 確率変数 $X_j$ は互いに独立であるため、この確率は、 \begin{align} G_3 \left(x\right)&=P \left(U_1 \le x\right) \cdot P \left(U_2 \le x\right) \cdot P \left(U_3 \le x\right)\\ &=F \left(x\right) \cdot F \left(x\right) \cdot F \left(x\right)\\ &= \left\{F \left(x\right)\right\}^3\\ &=x^3 \end{align} 累積分布関数と確率密度関数の関係 $g \left(x\right)=\frac{d}{dx}G \left(x\right)$ より、 \begin{align} g_3 \left(x\right)=3x^2 \end{align}

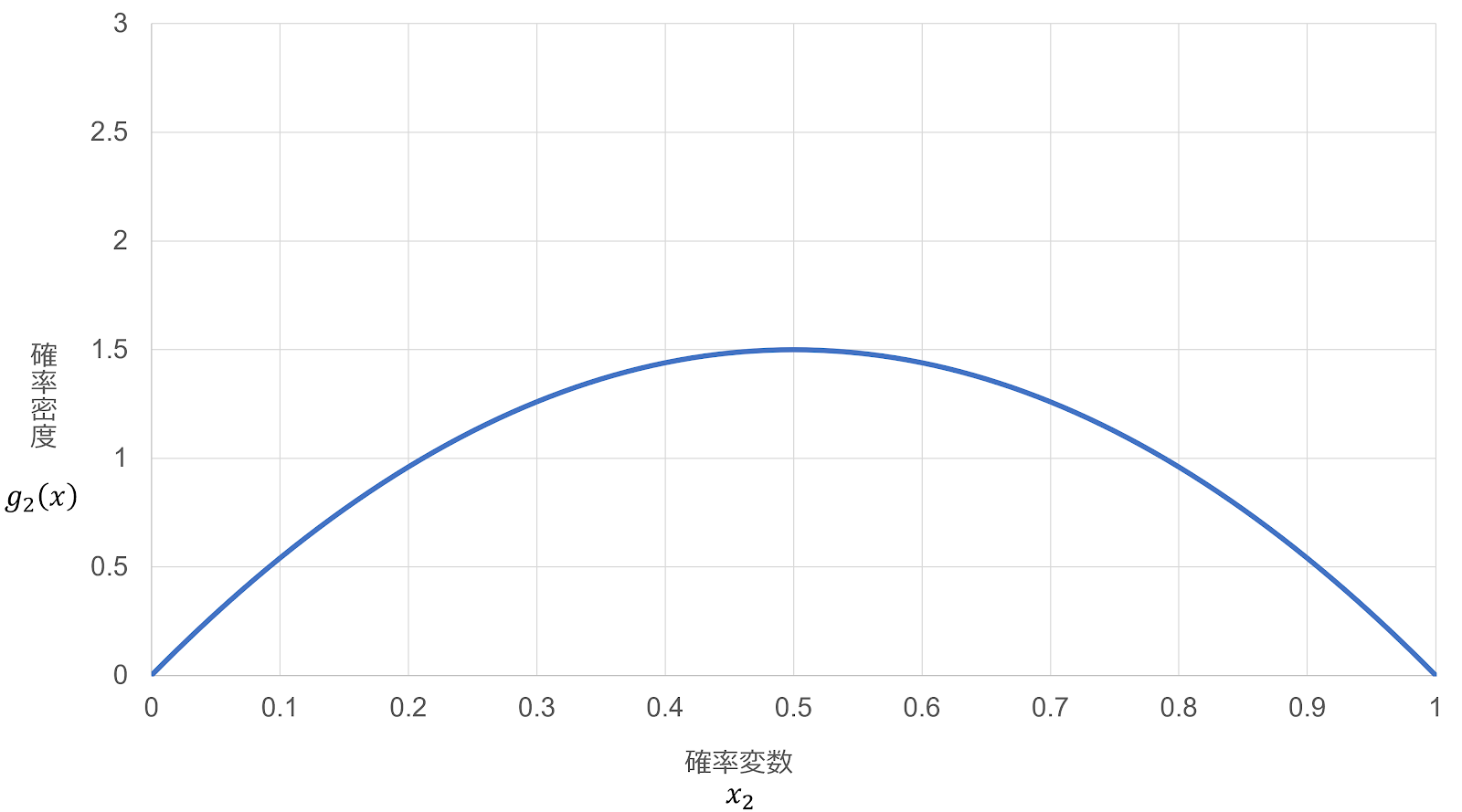
（ii）2番目に大きい値 $X_2$ の分布
2番目の値が $x$ 以下となるのは、
$U_1,\ U_2,U_3$ のうち2つが $x$ 以下、かつ、1つが $x$ 以上 もしくは、 $U_1,\ U_2,U_3$ のすべてが $x$ 以下 のときであるから、 （a）2つが $x$ 以下となる確率は、 \begin{align} P_1&={}_{3}C_2 \cdot P \left(U \le x\right) \cdot P \left(U \le x\right) \cdot P \left(U \geq x\right)\\ &=3 \cdot x \cdot x \cdot \left(1-x\right)\\ &=3x^2-3x^3 \end{align} （b）3つが $x$ 以下となる確率は、（i）の結果より、 \begin{align} P_2&=x^3 \end{align} したがって、 \begin{align} G_2 \left(x\right)&=3x^2-3x^3+x^3\\ &=3x^2-2x^3 \end{align} 累積分布関数と確率密度関数の関係 $g \left(x\right)=\frac{d}{dx}G \left(x\right)$ より、 \begin{align} g_2 \left(x\right)&=-6x^2+6x \end{align}

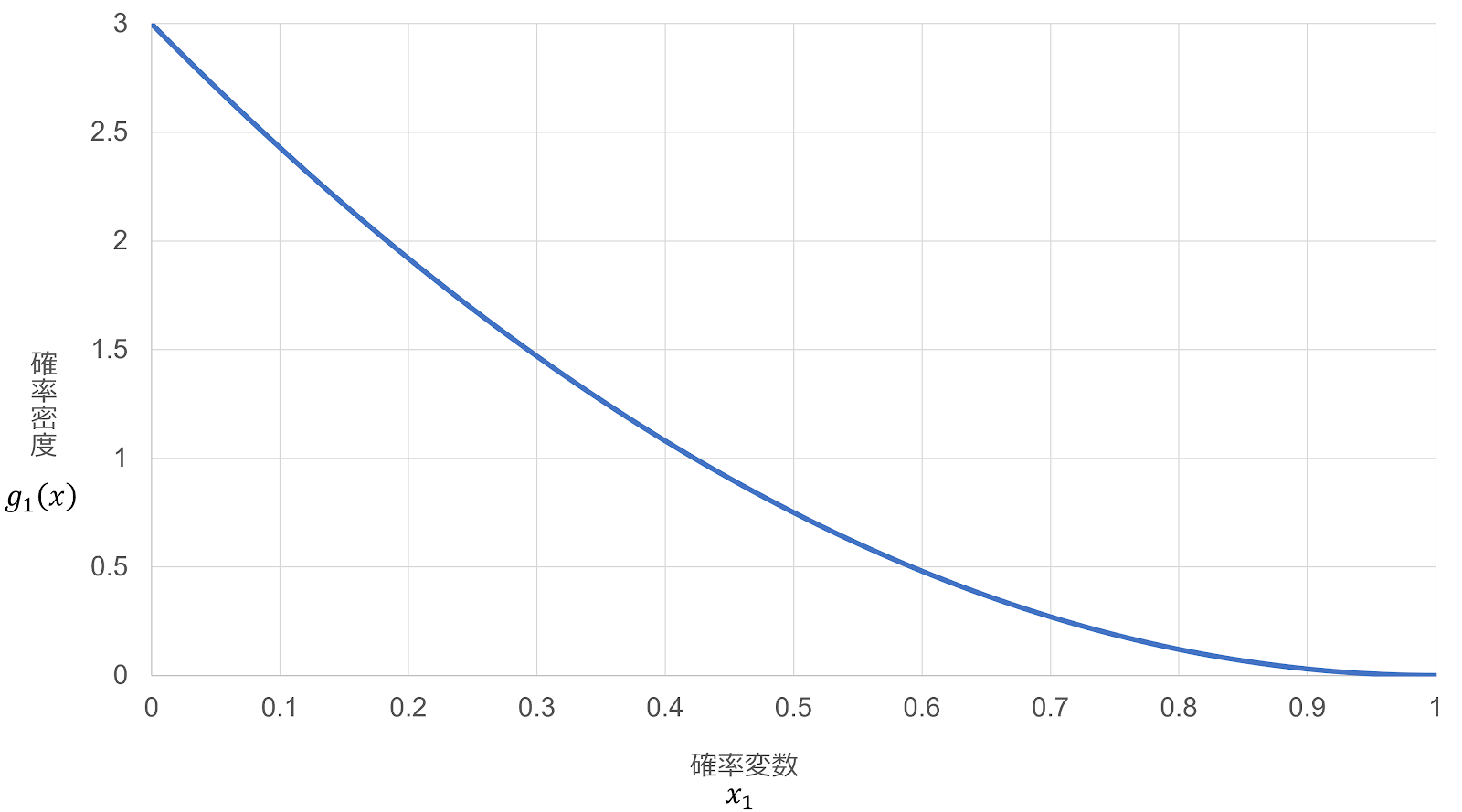
（iii）最小値 $X_1$ の分布
最小値が $x$ 以下となるとき、少なくとも1つの $X_i$ が $x$ 以下となる。これは、「すべての $X_i$ が $x$ 以上となる事象」の余事象であるから、 \begin{align} G_1 \left(x\right)=1-P \left(x \le X_1,x \le X_2,x \le X_3\right) \end{align} 確率変数 $X_j$ は互いに独立であるため、この確率は、 \begin{align} G_1 \left(x\right)=1-P \left(x \le U_1\right) \cdot P \left(x \le U_2\right) \cdot P \left(x \le U_3\right) \end{align} 確率の基本性質 $P \left(x \le X\right)=1-P \left(X \le x\right)$ より、 \begin{align} G_1 \left(x\right)&=1- \left[ \left\{1-F \left(x\right)\right\} \cdot \left\{1-F \left(x\right)\right\} \cdot \left\{1-F \left(x\right)\right\}\right]\\ &=1- \left\{1-F \left(x\right)\right\}^3\\ &=1- \left(1-x\right)^3 \end{align} 累積分布関数と確率密度関数の関係 $g \left(x\right)=\frac{d}{dx}G \left(x\right)$ より、 \begin{align} g_1 \left(x\right)&=-3 \left(1-x\right)^2 \cdot \frac{d}{dx} \left(1-x\right)\\ &=-3 \left(1-x\right)^2 \cdot \left(-1\right)\\ &=3 \left(1-x\right)^2 \end{align}

それぞれのグラフを描くと、以下のようになる。 $\blacksquare$

〔3〕確率変数の期待値

期待値の定義式 $E \left(X\right)=\int_{-\infty}^{\infty}{x \cdot f \left(x\right)dx}$ より、
（i）最大値 $X_3$ の期待値 \begin{align} E \left(X_3\right)&=\int_{0}^{1}{x \cdot g_3 \left(x\right)dx}\\ &=\int_{0}^{1}{x \cdot 3x^2dx}\\ &=\int_{0}^{1}{3x^3dx}\\ &= \left[\frac{3}{4}x^4\right]_0^1\\ &=\frac{3}{4} \end{align}

（ii）2番目に大きい値 $X_2$ の期待値
\begin{align} E \left(X_2\right)&=\int_{0}^{1}{x \cdot g_2 \left(x\right)dx}\\ &=\int_{0}^{1}x \left(-6x^2+6x\right)dx\\ &=\int_{0}^{1} \left(-6x^3+6x^2\right)dx\\ &= \left[-\frac{3}{2}x^4+2x^3\right]_0^1\\ &=-\frac{3}{2}+2\\ &=\frac{1}{2} \end{align}

（iii）最小値 $X_1$ の期待値 \begin{align} E \left(X_1\right)&=\int_{0}^{1}{x \cdot g_1 \left(x\right)dx}\\ &=\int_{0}^{1}x \left(3x^2-6x+3\right)dx\\ &=\int_{0}^{1} \left(3x^3-6x^2+3x\right)dx\\ &= \left[\frac{3}{4}x^4-2x^3+\frac{3}{2}x^2\right]_0^1\\ &=\frac{3}{4}-2+\frac{3}{2}\\ &=\frac{1}{4} \end{align} $\blacksquare$

関連記事

• 確率分布の特性値
• 確率積分変換
• 順序統計量の分布
• 最大値・最小値の分布