本稿には、2016年に実施された統計検定1級『医薬生物学』 問3の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。
- 著作権の関係上、問題文は、掲載することができません。申し訳ありませんが、閲覧者のみなさまでご用意いただければ幸いです。
- この答案は、あくまでも筆者が自作したものであり、公式なものではありません。正式な答案については、公式問題集をご参照ください。
- 計算ミスや誤字・脱字などがありましたら、コメントなどでご指摘いただければ大変助かります。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
〔1〕カプラン・マイヤー法による生存関数の推定
それぞれの群の瞬間ハザードと累積生存率を求めると、次のようになる。
観察時間
(週)打ち切り
イベント瞬間死亡率 累積生存率
$3$ $1$ $\frac{0}{5}$ $\frac{5}{5}=1$
$5$ $1$ $\frac{0}{4}$ $1\times\frac{4}{4}=1$
$7$ $1$ $\frac{0}{3}$ $1\times\frac{3}{3}=1$
$9$ $0$ $\frac{1}{2}$ $1\times\frac{1}{2}=\frac{1}{2}$
$10$ $0$ $\frac{1}{1}$ $\frac{1}{2}\times\frac{0}{1}=0$
これをもとにカプラン・マイヤー曲線を描くと次のようになる。
観察時間
(週)打ち切り
イベント瞬間死亡率 累積生存率
$1$ $0$ $\frac{1}{5}$ $\frac{4}{5}$
$2$ $0$ $\frac{1}{4}$ $\frac{4}{5}\times\frac{3}{4}=\frac{3}{5}$
$4$ $1$ $\frac{0}{3}$ $\frac{3}{5}\times\frac{3}{3}=\frac{3}{5}$
$5$ $0$ $\frac{1}{2}$ $\frac{3}{5}\times\frac{1}{2}=\frac{3}{10}$
$8$ $0$ $\frac{1}{1}$ $\frac{3}{10}\times0=0$ 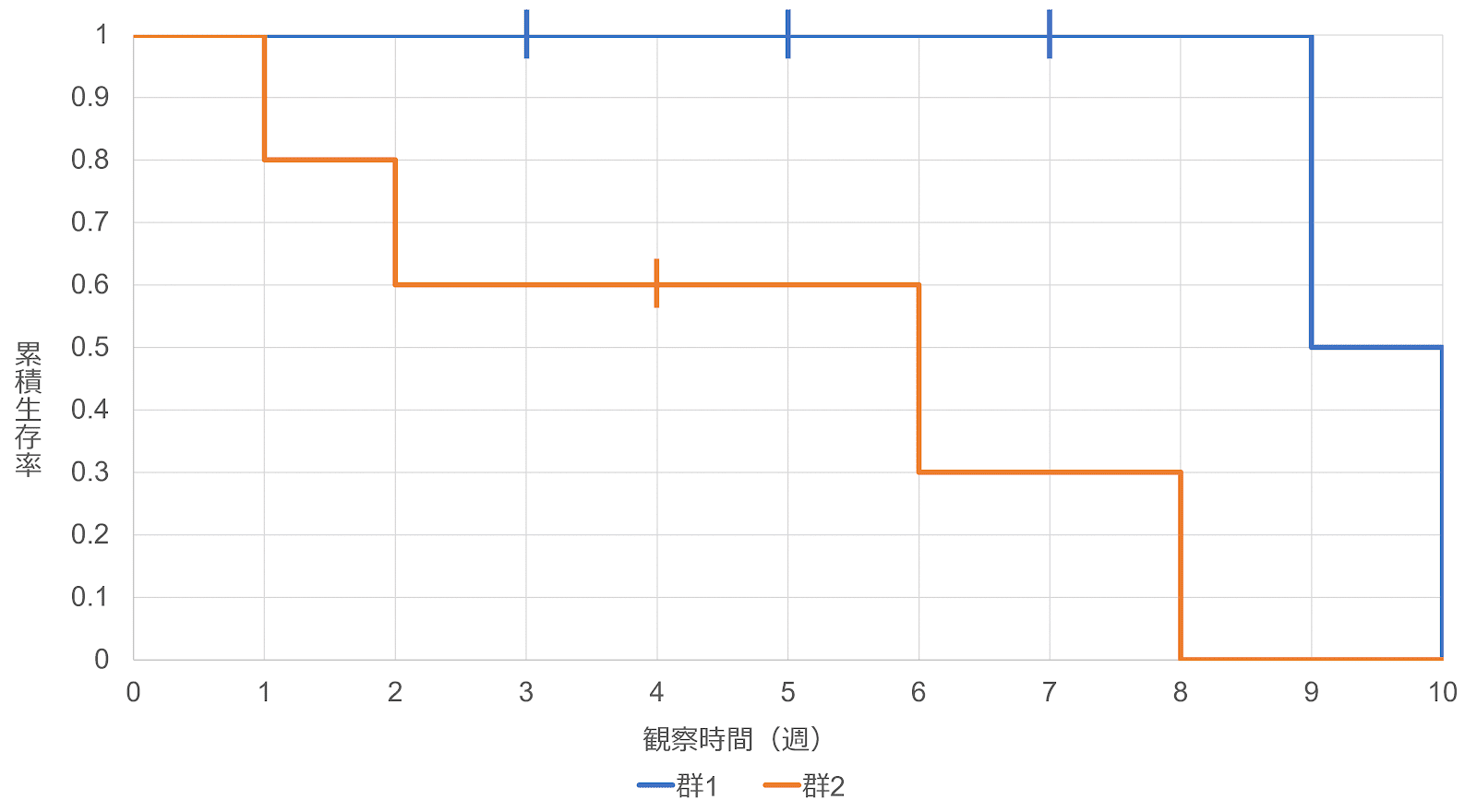
〔2〕ログランク検定
$i \left(=1,2,6,8,9,10\right)$ をイベントが発生した時点、$j \left(=1,2\right)$ を群番号を表すものとし、時点 $i$ における群 $j$ の値を以下のように定義する。
- $d_{ij}$:イペント発生数
- $n_{ij}$:リスク集合の大きさ
- $e_{ij}$:イペント発生数の期待値
- $d_i$:(群1と群2)全体でのイベント発生数
- $n_i$:(群1と群2)全体でのリスク集合の大きさ
このとき、イペント発生数の期待値は、
\begin{align}
e_{ij}=n_{ij}\times\frac{d_i}{n_i}
\end{align}
期待値と群 $j$ での(実際の)イベント発生数との差
\begin{align}
u_{ij}=d_{ij}-e_{ij}
\end{align}
を時点 $i$ におけるスコアとし、
このスコアを単純に合計したものが各群のスコア
\begin{align}
u=\sum_{i=1}^{10}u_{ij}
\end{align}
となる
(なお、各群のスコアは、符号が反対で絶対値は等しいため、どちらで求めてもよい)。
それぞれの時点でのスコア $u_{ij}$ の分散は、イベント数が $d_i=1$ の場合は、
\begin{align}
V \left(u_i\right)=\frac{n_{i1} \cdot n_{i2}}{n_i^2}
\end{align}
それぞれの時点でのスコアが互いに独立であるとすると、分散の性質より、
\begin{align}
V \left(u\right)=\sum_{i=1}^{10}V \left(u_i\right)
\end{align}
こうしたことをもとに、各時点でのスコアとスコアの分散を算出すると、以下のようになる。
| $t_i$ | $d_{i1}$ | $d_{i2}$ | $n_{i1}$ | $n_{i2}$ | $n_i$ | $e_{i1}$ | $e_{i2}$ | $u_{i1}$ | $u_{i2}$ | $V \left(u_i\right)$ |
|---|---|---|---|---|---|---|---|---|---|---|
| $1$ | $0$ | $1$ | $5$ | $5$ | $10$ | $5\times\frac{1}{10}=\frac{1}{2}$ | $5\times\frac{1}{10}=\frac{1}{2}$ | $0-\frac{1}{2}=-\frac{1}{2}$ | $1-\frac{1}{2}=\frac{1}{2}$ | $\frac{5}{10}\times\frac{5}{10}=\frac{1}{4}$ |
| $2$ | $0$ | $1$ | $5$ | $4$ | $9$ | $5\times\frac{1}{9}=\frac{5}{9}$ | $4\times\frac{1}{9}=\frac{4}{9}$ | $0-\frac{5}{9}=-\frac{5}{9}$ | $1-\frac{4}{9}=\frac{5}{9}$ | $\frac{5}{9}\times\frac{4}{9}=\frac{20}{81}$ |
| $6$ | $0$ | $1$ | $3$ | $2$ | $5$ | $3\times\frac{1}{5}=\frac{3}{5}$ | $2\times\frac{1}{5}=\frac{2}{5}$ | $0-\frac{3}{5}=-\frac{3}{5}$ | $1-\frac{2}{5}=\frac{3}{5}$ | $\frac{3}{5}\times\frac{2}{5}=\frac{6}{25}$ |
| $8$ | $0$ | $1$ | $2$ | $1$ | $3$ | $2\times\frac{1}{3}=\frac{2}{3}$ | $1\times\frac{1}{3}=\frac{1}{3}$ | $0-\frac{2}{3}=-\frac{2}{3}$ | $1-\frac{1}{3}=\frac{2}{3}$ | $\frac{2}{3}\times\frac{1}{3}=\frac{2}{9}$ |
| $9$ | $1$ | $0$ | $2$ | $0$ | $2$ | $2\times\frac{1}{2}=1$ | $0\times\frac{1}{2}=0$ | $1-1=0$ | $0-0=0$ | $\frac{0}{2}\times\frac{2}{2}=0$ |
| $10$ | $1$ | $0$ | $1$ | $0$ | $1$ | $1\times\frac{1}{1}=1$ | $0\times\frac{1}{1}=0$ | $1-1=0$ | $0-0=0$ | $\frac{0}{1}\times\frac{1}{1}=0$ |
したがって、 \begin{align} u&=-\frac{1}{2}-\frac{5}{9}-\frac{3}{5}-\frac{2}{3}+0+0\\ &\cong-0.5-0.56-0.6-0.67\\ &=-2.33 \end{align} \begin{align} V \left(u\right)&=\frac{1}{4}+\frac{20}{81}+\frac{6}{25}+\frac{2}{9}+0+0\\ &\cong0.25+0.25+0.24+0.22\\ &=0.96 \end{align} したがって、ログランク検定の検定統計量は、 \begin{align} \chi^2=\frac{u^2}{V \left(u\right)}=\frac{ \left(-2.33\right)^2}{0.96}\cong5.62 \end{align} 帰無仮説のもとで、 \begin{align} \chi^2 \sim \chi^2 \left(1\right) \quad Z=\sqrt{\chi^2} \sim \mathrm{N} \left(0,1\right) \end{align} 付表1より、 \begin{align} \sqrt{5.62}=2.3712\cong Z_{0.0089} \left(n\right) \end{align} したがって、両側p値は、 \begin{align} p\cong0,0089\times2=0.0178 \end{align} $\blacksquare$
〔3〕コックス比例ハザードモデルの部分尤度
時点 $i$ における各群のハザードは、
\begin{gather}
h_1=h \left(0,t\right)=h_0 \left(t\right)e^0=h_0 \left(t\right)\\
h_2=h \left(1,t\right)=h_0 \left(t\right)e^{\beta \cdot 1}=h_0 \left(t\right)e^\beta
\end{gather}
このとき、確率の乗法定理により、
「時点 $t_{ \left(i\right)}$ で群 $j$ の1人にイベントが起きる確率」=「時点 $t_{ \left(i\right)}$ でイベントが1件起きる確率」×「時点 $t_{ \left(i\right)}$ でイベントが起きたという条件付きでそれが群 $j$ の1人である確率」
\begin{align}
P \left(d_{ij}=1\right)=P \left(d_i=1\right)\times P \left(d_{ij}=1\middle| d_i=1\right)
\end{align}
部分尤度は、このうち「時点 $t_{ \left(i\right)}$ でイベントが起きたという条件付きでそれが群 $j$ の1人である確率」に関する尤度のことを指し、
\begin{align}
L=\prod_{i=1}^{k}\frac{h \left(i\right)}{\sum_{j=1}^{n_i}h_\boldsymbol{j}}
\end{align}
この問題では、群2→群2→群2→群2→群1→群1という順番でイベントが発生しているが、例えば、最初の事象が起こる確率は、群1が5人、群2に5人、at riskの人(ハザードに暴露されている人)がいて、イベントが1件発生した際、それが群2の1人である確率(=全体のハザードの中で群2の1人のハザードが占める割合)なので、
\begin{align}
L=\frac{h_2}{5h_1+5h_2}
\end{align}
以下同様に考えていくと、全体としての部分尤度は、
\begin{align}
L&=\frac{h_2}{5h_1+5h_2}\times\frac{h_2}{5h_1+4h_2}\times\frac{h_2}{3h_1+2h_2}\times\frac{h_2}{2h_1+h_2}\times\frac{h_1}{2h_1+0}\times\frac{h_1}{h_1+0}\\
&=\frac{h_0 \left(t\right)}{h_0 \left(t\right)} \left(\frac{5e^\beta}{5+5e^\beta}\times\frac{4e^\beta}{5+4e^\beta}\times\frac{2e^\beta}{3+2e^\beta}\times\frac{e^\beta}{2+e^\beta}\times\frac{1}{2}\times\frac{1}{1}\right)\\
&=\frac{5e^\beta}{5+5e^\beta}\times\frac{4e^\beta}{5+4e^\beta}\times\frac{2e^\beta}{3+2e^\beta}\times\frac{e^\beta}{2+e^\beta}\times\frac{1}{2}\times\frac{1}{1}
\end{align}
$\blacksquare$



0 件のコメント:
コメントを投稿