統計検定 1級 2019年 医薬生物学 問1 生存時間分析：境界内平均生存時間

本稿には、2019年に実施された統計検定1級『医薬生物学』 問1の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。

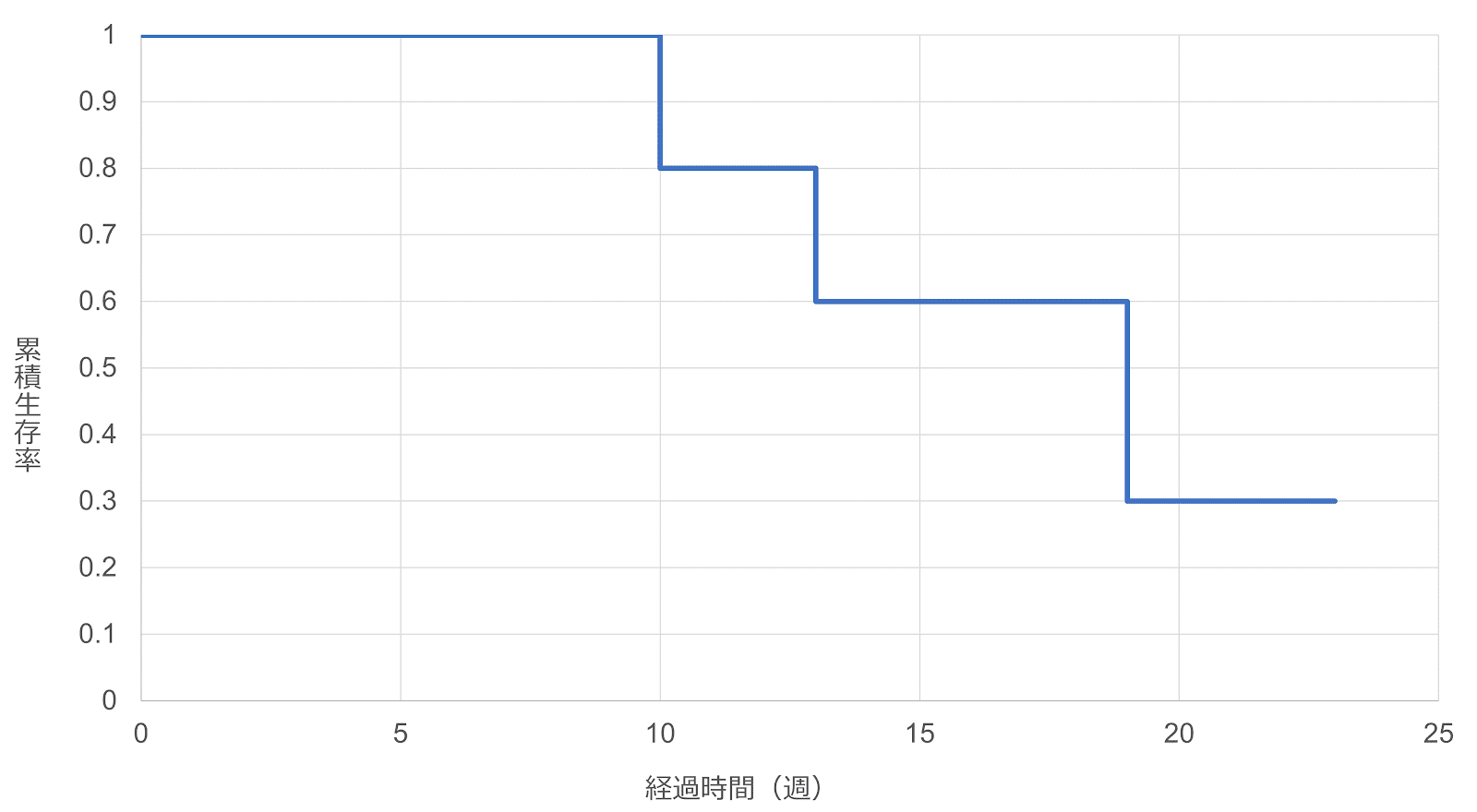
〔1〕カプラン・マイヤー法による生存関数の推定

与えられたデータにもとづいて表2を作成すると、以下のようになる。

これをもとにカプラン・マイヤー法による生存曲線を描くと、以下のようになる。

〔2〕カプラン・マイヤー推定値とネルソン・アーレン推定値の関係

時点 $t$ におけるカプラン・マイヤー法により推定された生存関数の推定値 $\hat{S}\left(t\right)$ は、 $$\begin{array}{r}\hat{S}\left(t\right)=\prod _{k=1}^j(1-\frac{d_k}{n_k})\end{array}$$ いっぽう、生存関数のネルソン・アーレン推定値は、 $$\begin{array}{r}\tilde{S}\left(t\right)=\prod _{k=1}^j\exp (-\frac{d_k}{n_k})\end{array}$$ ここで、以下のような関数を考えると、 $$\begin{array}{c}f\left(x\right)=e^{-x}-(1-x)\\ x=\frac{d_k}{n_k}\end{array}$$ $f\left(x\right)$ の1次導関数 $f^{\prime }\left(x\right)$ は、 $$\begin{array}{r}{f}^{\prime }\left(x\right)=1--e^{-x}\end{array}$$ 増減表は、 $$\begin{array}{cccc}x& \cdots & 0& \cdots \\ f^{\prime }\left(x\right)& -& 0& +\\ f\left(x\right)& \searrow & 0& \nearrow \end{array}$$ したがって、$0\le x$ となる任意の点において、 $$\begin{array}{r}{e}^{-x}\ge 1-x\end{array}$$ これにより、 $$\begin{array}{c}\exp (-\frac{d_k}{n_k})\ge 1-\frac{d_k}{n_k}\\ \prod _{k=1}^j\exp (-\frac{d_k}{n_k})\ge \prod _{k=1}^j(1-\frac{d_k}{n_k})\\ \tilde{S}\left(t\right)\ge \hat{S}\left(t\right)\end{array}$$ $◼$

〔3〕境界内平均生存時間の性質

$T$ の確率密度関数、累積分布関数、生存関数をそれぞれ以下のようにおく。 $$\begin{array}{r}f\left(t\right)F\left(t\right)S\left(t\right)\end{array}$$ 期待値の定義式 $E\left(X\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}x\cdot f\left(x\right)dx$ より、 $$\begin{array}{rl}E\left\{X\left(\tau \right)\right\}& =E\left\{\min (T,\tau )\right\}\\ & ={\int }_0^{\tau }t\cdot f\left(t\right)dt+{\int }_{\tau }^{\mathrm{\infty }}\tau \cdot f\left(t\right)dt\\ & ={[t\cdot F\left(t\right)]}_0^{\tau }-{\int }_0^{\tau }F\left(t\right)dt+{\tau \left[F\left(t\right)\right]}_{\tau }^{\mathrm{\infty }}\\ & =\tau F\left(\tau \right)-{\int }_0^{\tau }\{1-S\left(t\right)\}dt+\tau \{1-F\left(\tau \right)\}\\ & ={[-t]}_0^{\tau }+{\int }_0^{\tau }S\left(t\right)dt+\tau \\ & =-\tau +{\int }_0^{\tau }S\left(t\right)dt+\tau \\ & ={\int }_0^{\tau }S\left(t\right)dt\end{array}$$ 以上より、境界内平均生存時問は、境界時間 $\tau$ 内における生存曲線の曲線下面積に等しい。 $◼$

〔4〕境界内平均生存時間の分散

〔3〕の結果に生存関数 $S\left(t\right)=e^{-\lambda t}$ を代入すると、 $$\begin{array}{rl}E\left\{X\left(\tau \right)\right\}& ={\int }_0^{\tau }S\left(t\right)dt\\ & ={\int }_0^{\tau }{e}^{-\lambda t}dt\\ & ={[-\frac{1}{\lambda }{e}^{-\lambda t}]}_0^{\tau }\\ & =\frac{1-e^{-\lambda \tau }}{\lambda }\end{array}$$ 2乗の期待値の定義式 $E\left(X^2\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{x}^2\cdot f\left(x\right)dx$ より、 $$\begin{array}{rl}E\left\{X^2\left(\tau \right)\right\}& ={\int }_0^{\tau }{t}^2\cdot f\left(t\right)dt+{\int }_{\tau }^{\mathrm{\infty }}{\tau }^2\cdot f\left(t\right)dt\\ & ={\left[t^{2}F\left(t\right)\right]}_0^{\tau }-{\int }_0^{\tau }2tF\left(t\right)dt+{{\tau }^2\left[F\left(t\right)\right]}_{\tau }^{\mathrm{\infty }}\\ & ={\tau }^{2}F\left(\tau \right)-{\int }_0^{\tau }2t\{1-S\left(t\right)\}dt+{\tau }^2\{1-F\left(\tau \right)\}\\ & ={[-t^2]}_0^{\tau }+2{\int }_0^{\tau }t\cdot S\left(t\right)dt+{\tau }^2\\ & =-{\tau }^2+2{\int }_0^{\tau }t\cdot S\left(t\right)dt+{\tau }^2\\ & =2{\int }_0^{\tau }t\cdot S\left(t\right)dt\\ & =2{\int }_0^{\tau }t\cdot e^{-\lambda t}dt\\ & =2{[-\frac{t}{\lambda }{e}^{-\lambda t}]}_0^{\tau }+2{\int }_0^{\tau }\frac{e^{-\lambda t}}{\lambda }dt\\ & =-\frac{2\tau e^{-\lambda \tau }}{\lambda }+\frac{2(1-e^{-\lambda \tau })}{{\lambda }^2}\\ & =\frac{2-2\lambda \tau e^{-\lambda \tau }-2e^{-\lambda \tau }}{{\lambda }^2}\end{array}$$ 分散の公式 $V\left(X\right)=E\left(X^2\right)-{\left\{E\left(X\right)\right\}}^2$ より、 $$\begin{array}{rl}V\left\{X\left(\tau \right)\right\}& =\frac{2-2\lambda \tau e^{-\lambda \tau }-2e^{-\lambda \tau }}{{\lambda }^2}-\frac{1-2e^{-\lambda t}+e^{-2\lambda t}}{{\lambda }^2}\\ & =\frac{1-2\lambda \tau e^{-\lambda \tau }-e^{-2\lambda \tau }}{{\lambda }^2}\end{array}$$ $◼$

〔5〕ハザード・境界内平均生存時間の最尤推定値

生存関数に関する仮定より、 $$\begin{array}{c}S\left(t\right)=1-F\left(t\right)=e^{-\lambda t}\\ F\left(t\right)=1-e^{-\lambda t}\end{array}$$ 累積分布関数と確率密度関数の関係 $f\left(x\right)=\frac{d}{dx}F\left(x\right)$ より、 $$\begin{array}{r}f\left(t\right)=\lambda e^{-\lambda t}\end{array}$$ イベント時間の尤度関数の定義式より、 $$\begin{array}{r}L\left(\lambda \right)=\prod _{i=1}^n{\left[f\left(t_i\right)\right]}^{{\delta }_i}{\left[S\left(t_i\right)\right]}^{1-{\delta }_i}\end{array}$$ イベント時間の確率密度関数、ハザード関数、生存関数の関係 $f\left(t\right)=\lambda \left(t\right)\cdot S\left(t\right)$ より、 $$\begin{array}{rl}L\left(\lambda \right)& =\prod _{i=1}^n{\left[f\left(t_i\right)\right]}^{{\delta }_i}{\left[S\left(t_i\right)\right]}^{1-{\delta }_i}\\ & =\prod _{i=1}^n{\left[\lambda e^{-\lambda t_i}\right]}^{{\delta }_i}{\left[e^{-\lambda t_i}\right]}^{1-{\delta }_i}\\ & =\prod _{i=1}^n{\lambda }^{{\delta }_i}\cdot e^{-\lambda t_i}\end{array}$$ 対数尤度関数 $l\left(\theta \right)=\log L\left(\theta \right)$ を求めると、 $$\begin{array}{r}l\left(\lambda \right)=\sum _{i=1}^n{\delta }_i\log \lambda -\lambda \sum _{i=1}^n{t}_i\end{array}$$ スコア関数 $S\left(\theta \right)=\frac{d}{d\theta }\log L\left(\theta \right)$ を求めると、 $$\begin{array}{rl}S\left(\lambda \right)& =\frac{1}{\lambda }\sum _{i=1}^n{\delta }_i-\sum _{i=1}^n{t}_i\\ & =\frac{\delta }{\lambda }-\sum _{i=1}^n{t}_i\end{array}$$ 尤度方程式 $S\left(\theta \right)=0$ を解くと、 $$\begin{array}{c}0=\frac{\delta }{\hat{\lambda }}-\sum _{i=1}^n{t}_i\\ \frac{\delta }{\hat{\lambda }}=\sum _{i=1}^n{t}_i\\ \hat{\lambda }=\frac{\delta }{\sum _{i=1}^n{t}_i}\end{array}$$ したがって、表1 のデータから最尤推定値は、 $$\begin{array}{r}\hat{\lambda }=\frac{3}{10+13+18+19+23}=\frac{3}{83}\cong 0.036\end{array}$$ 〔4〕の結果より、$\tau =20$ とした境界内平均生存時間とその分散の推定値は、付表5の値を用いると $$\begin{array}{rl}\hat{E}\left\{X\left(\tau \right)\right\}& =\frac{1-e^{-0.036\cdot 20}}{0.036}\\ & =\frac{1-e^{-0.72}}{0.036}\\ & =\frac{1-\frac{1}{e^{0.72}}}{0.036}\\ & =\frac{1-\frac{1}{2.0544}}{0.036}\\ & =\frac{0.513}{0.036}\\ & \cong 14.25\end{array}$$ $$\begin{array}{rl}\hat{V}\left\{X\left(\tau \right)\right\}& =\frac{1-2\cdot 0.036\cdot 20\cdot e^{-0.036\cdot 20}-e^{-2\cdot 0.036\cdot 20}}{{0.036}^2}\\ & =\frac{1-2\cdot 0.036\cdot 20\cdot e^{-0.72}-e^{-2\cdot 0.72}}{{0.036}^2}\\ & =\frac{1-\frac{2\cdot 0.036\cdot 20}{2.0544}-\frac{1}{{2.0544}^2}}{{0.036}^2}\\ & =\frac{0.0621}{0.0013}\\ & \cong 47.69\end{array}$$ $◼$

関連記事

• 生存関数の推定
• カプラン・マイヤー法
• 生存時間分布のパラメトリックモデル①：指数分布モデル