統計検定 1級 2022年 統計数理 問2 二変数確率変数

本稿には、2022年に実施された統計検定1級『統計数理』 問2の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。

〔1〕周辺分布関数

周辺分布関数の定義より、$U$ の分布関数は、 \begin{align} F_1 \left(u\right)&=\frac{1}{4}\int_{-1}^{1} \left(uv+u+v+1\right)dv\\ &=\frac{1}{4} \left[\frac{1}{2} \left(u+1\right)v^2+ \left(u+1\right)v\right]_{-1}^1\\ &=\frac{u+1}{4} \left\{ \left(\frac{1}{2}+1\right)- \left(\frac{1}{2}-1\right)\right\}\\ &=\frac{u+1}{2} \end{align} $V$ の分布関数も同様に（$U$ と $V$ の対称性から）、 \begin{align} F_2 \left(v\right)=\frac{v+1}{2} \end{align} これらは、区間 $ \left[-1,1\right]$ の連続一様分布の分布関数であるから、分布関数の一意性により、$U,V$ は共に連続一様分布に従う。 $\blacksquare$

〔2〕確率変数の独立性

周辺分布関数の積を計算すると、 \begin{align} F_1 \left(u\right) \cdot F_2 \left(v\right)&=\frac{u+1}{2} \cdot \frac{v+1}{2}\\ &=\frac{uv+u+v+1}{4}\\ &=F \left(u,v\right) \end{align} したがって、確率変数の独立性の定義を満たすので、$U,V$ は互いに独立である。このとき、$ \left(U,V\right)$ は正方形 $ \left[-1,1\right]\times \left[-1,1\right]$ 上の一様分布に従う。 $\blacksquare$

〔3〕確率変数の関数の確率①

$U,V$ 平面上の正方形 $ \left[-1,1\right]\times \left[-1,1\right]$ と原点を中心とする単位円について考えると、単位円の方程式は、 \begin{align} U^2+V^2=1 \end{align} このとき、領域 $U^2+V^2 \le 1$ は、単位円の内側（境界線を含む）の面積なので、 \begin{align} S_1=\pi \end{align}

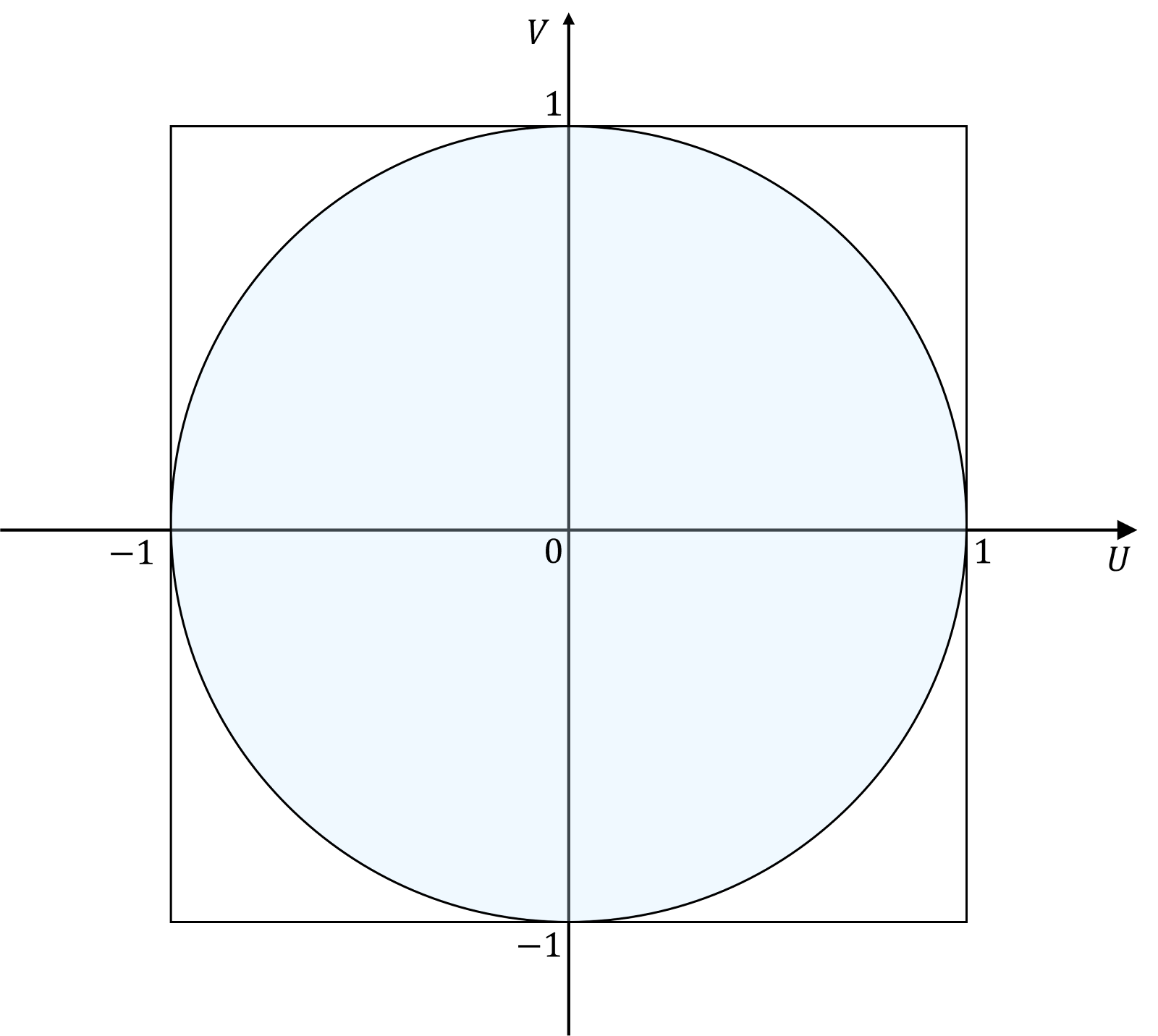
いっぽう、同時確率変数 $ \left(U,V\right)$ が取り得る領域の面積は、 \begin{align} S=2\times2=4 \end{align} このとき、確率 $P \left(U^2+V^2 \le 1\right)$ は、正方形の面積に占める単位円の面積の割合と考えることができるので、 \begin{align} P \left(U^2+V^2 \le 1\right)=\frac{\pi}{4} \end{align} $\blacksquare$

〔4〕確率変数の関数の確率②

求める確率の式を変形すると、 \begin{align} P \left(U^2-2UV+V^2 \le 1\right)&=P \left\{ \left(U-V\right)^2 \le 1\right\}\\ &=P \left(-1 \le U-V \le 1\right)\\ &=P \left(U-1 \le V \le U+1\right) \end{align} $U,V$ 平面上における領域 $ \left(U-1 \le V \le U+1\right) \cap \left(-1 \le U,V \le 1\right)$ の面積は、 \begin{align} S_2=4-1\times1\times\frac{1}{2}\times2=3 \end{align}

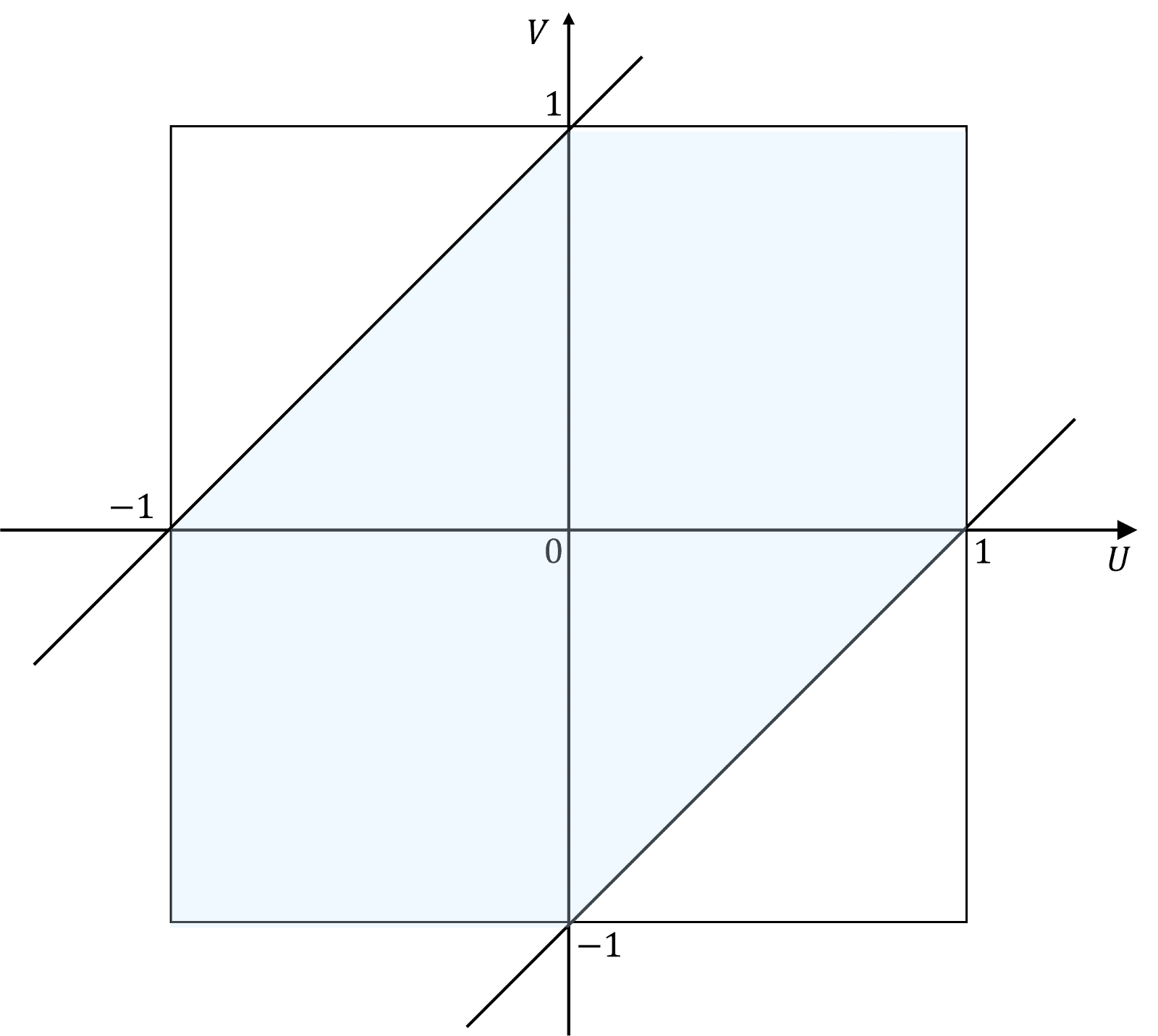
したがって、〔3〕と同様に、正方形の面積に占める領域の面積の割合として、 \begin{align} P \left(U^2-2UV+V^2 \le 1\right)=\frac{3}{4} \end{align} $\blacksquare$

〔5〕条件付き期待値・分散・相関係数

同時分布関数と同時確率密度関数の関係より、 \begin{align} f \left(u,v\right)&=\frac{\partial^2}{\partial u\partial v}F \left(u,v\right)\\ &=\frac{1}{4} \end{align} 〔4〕の条件の下での同時確率密度関数は、 \begin{align} f \left(u,v\middle| U^2-2UV+V^2 \le 1\right)&=\frac{f \left(u,v\right)}{P \left(U^2-2UV+V^2 \le 1\right)}\\ &=\frac{1}{4} \cdot \frac{4}{3}\\ &=\frac{1}{3} \end{align} 以下、 \begin{align} f \left(u,v\middle| U^2-2UV+V^2 \le 1\right)\Rightarrow f \left(u,v\middle| C\right) \end{align} と略記する。

ここで、条件付き分布における $U,V$ の値域について検討すると、 \begin{gather} -1 \le u \le 1 \quad -1 \le v \le 1\\ u-1 \le v \le u+1 \end{gather} $v$ については、$u$ の値によって場合分けが必要となり、 \begin{gather} u-1 \le -1\Leftrightarrow \left(-1 \le \right)u \le 0\\ \Rightarrow-1 \le v \le u+1 \end{gather} \begin{gather} 1 \le u+1\Leftrightarrow0 \le u \left( \le 1\right)\\ \Rightarrow u-1 \le v \le 1 \end{gather}

期待値の定義 $E \left(X\right)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}{x \cdot f \left(x,y\right)dxdy}$ より、 \begin{align} E \left(V\middle| C\right)&=\int_{-1}^{0}\int_{-1}^{u+1}{v \cdot f \left(u,v\middle| C\right)dudv}+\int_{0}^{1}\int_{u-1}^{1}{v \cdot f \left(u,v\middle| C\right)dudv}\\ &=\frac{1}{3} \left(\int_{-1}^{0}\int_{-1}^{u+1}{v \cdot d u d v}+\int_{0}^{1}\int_{u-1}^{1}{v \cdot d u d v}\right)\\ &=\frac{1}{6} \left(\int_{-1}^{0}{ \left[v^2\right]_{-1}^{u+1}du}+\int_{0}^{1}{ \left[v^2\right]_{u-1}^1du}\right)\\ &=\frac{1}{6} \left(\int_{-1}^{0} \left(u^2+2u\right)du-\int_{0}^{1} \left(u^2-2u\right)du\right)\\ &=\frac{1}{6} \left( \left[\frac{1}{3}u^3+u^2\right]_{-1}^0- \left[\frac{1}{3}u^3-u^2\right]_0^1\right)\\ &=\frac{1}{6} \left[ \left(\frac{1}{3}-1\right)- \left(\frac{1}{3}-1\right)\right]\\ &=0 \end{align} $U,V$ の対称性から、 \begin{align} E \left(U\middle| C\right)&=0 \end{align}

期待値の定義 $E \left[h \left(X\right)\right]=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}{h \left(x\right) \cdot f \left(x,y\right)dxdy}$ より、 \begin{align} E \left(V^2\middle| C\right)&=\int_{-1}^{0}\int_{-1}^{u+1}{v^2 \cdot f \left(u,v\middle| C\right)dudv}+\int_{0}^{1}\int_{u-1}^{1}{v^2 \cdot f \left(u,v\middle| C\right)dudv}\\ &=\frac{1}{3} \left(\int_{-1}^{0}\int_{-1}^{u+1}{v^2 \cdot d u d v}+\int_{0}^{1}\int_{u-1}^{1}{v^2 \cdot d u d v}\right)\\ &=\frac{1}{9} \left(\int_{-1}^{0}{ \left[v^3\right]_{-1}^{u+1}du}+\int_{0}^{1}{ \left[v^3\right]_{u-1}^1du}\right)\\ &=\frac{1}{9} \left(\int_{-1}^{0} \left(u^3+3u^2+3u+2\right)du-\int_{0}^{1} \left(u^3-3u^2+3u-2\right)du\right)\\ &=\frac{1}{9} \left( \left[\frac{1}{4}u^4+u^3+\frac{3}{2}u^2+2u\right]_{-1}^0- \left[\frac{1}{4}u^4-u^3+\frac{3}{2}u^2-2u\right]_0^1\right)\\ &=\frac{1}{9} \left[0- \left(\frac{1}{4}-1+\frac{3}{2}-2\right)- \left\{ \left(\frac{1}{4}-1+\frac{3}{2}-2\right)-0\right\}\right]\\ &=\frac{1}{9} \left(\frac{5}{4}+\frac{5}{4}\right)\\ &=\frac{5}{18} \end{align} 分散の公式 $V \left(X\right)=E \left(X^2\right)- \left\{E \left(X\right)\right\}^2$ より、 \begin{align} V \left(V\middle| C\right)=\frac{5}{18}-0=\frac{5}{18} \end{align} $U,V$ の対称性から、 \begin{align} V \left(U\middle| C\right)&=\frac{5}{18} \end{align}

期待値の定義 $E \left[h \left(X,Y\right)\right]=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}{h \left(x,y\right) \cdot f \left(x,y\right)dxdy}$ より、 \begin{align} E \left(UV\middle| C\right)&=\int_{-1}^{0}\int_{-1}^{u+1}{uv \cdot f \left(u,v\middle| C\right)dudv}+\int_{0}^{1}\int_{u-1}^{1}{uv \cdot f \left(u,v\middle| C\right)dudv}\\ &=\frac{1}{3} \left(\int_{-1}^{0}\int_{-1}^{u+1}{uv \cdot d u d v}+\int_{0}^{1}\int_{u-1}^{1}{uv \cdot d u d v}\right)\\ &=\frac{1}{6} \left(\int_{-1}^{0}{ \left[uv^2\right]_{-1}^{u+1}du}+\int_{0}^{1}{ \left[uv^2\right]_{u-1}^1du}\right)\\ &=\frac{1}{6} \left(\int_{-1}^{0} \left(u^3+2u^2\right)du-\int_{0}^{1} \left(u^3-2u^2\right)du\right)\\ &=\frac{1}{6} \left( \left[\frac{1}{4}u^4+\frac{2}{3}u^3\right]_{-1}^0- \left[\frac{1}{4}u^4-\frac{2}{3}u^3\right]_0^1\right)\\ &=\frac{1}{6} \left[0- \left(\frac{1}{4}-\frac{2}{3}\right)- \left\{ \left(\frac{1}{4}-\frac{2}{3}\right)-0\right\}\right]\\ &=\frac{1}{6} \left(\frac{5}{12}+\frac{5}{12}\right)\\ &=\frac{5}{36} \end{align}

共分散の公式 $\mathrm{Cov} \left(X,Y\right)=E \left(XY\right)-E \left(X\right)E \left(Y\right)$ より、 \begin{align} \mathrm{Cov} \left(U,V\middle| C\right)=\frac{5}{36}-0=\frac{5}{36} \end{align}

したがって、相関係数の定義 $\rho_{XY}=\frac{\mathrm{Cov} \left(X,Y\right)}{\sigma_X\sigma_Y}$ より、 \begin{align} \rho_{UV}=\frac{\frac{5}{36}}{\frac{5}{18}}=\frac{1}{2} \end{align} $\blacksquare$

関連記事

• 多次元の確率分布
• 共分散と相関係数
• 条件付き確率分布の特性値