本稿には、2018年に実施された統計検定1級『医薬生物学』 問3の自作解答案を掲載しています。なお、閲覧にあたっては、以下の点にご注意ください。
- 著作権の関係上、問題文は、掲載することができません。申し訳ありませんが、閲覧者のみなさまでご用意いただければ幸いです。
- この答案は、あくまでも筆者が自作したものであり、公式なものではありません。正式な答案については、公式問題集をご参照ください。
- 本記事は、〔3〕までの解答案となります。
- 計算ミスや誤字・脱字などがありましたら、コメントなどでご指摘いただければ大変助かります。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
〔1〕真陽性率と偽陽性率の算出
真の罹患状況と予測値から判断した検査結果の関係を表した2×2分割表を作成すると、以下のようになる。
| 陽性 $0.5 \le X$ | 陰性 $X \lt 0.5$ | 合計 | |
|---|---|---|---|
| 罹患あり | $5$ | $3$ | $8$ |
| 罹患なし | $3$ | $5$ | $8$ |
| 合計 | $8$ | $8$ | $16$ |
真陽性率の定義(罹患ありの中で、検査が陽性になる確率)より、 \begin{align} \mathrm{Sen}=\frac{5}{8} \end{align} また、特異度の定義(罹患なしの中で、検査が陰性になる確率)より、 \begin{align} \mathrm{Spe}=\frac{5}{8} \end{align} したがって、偽陽性率は、 \begin{align} \mathrm{FP}=1-\frac{5}{8}=\frac{3}{8} \end{align} $\blacksquare$
〔2〕ROC曲線の作成
疾病に罹患していると判断するカットオフ値と真陽性、偽陰性、偽陽性、真陰性の関係を調べると以下のようになる。
|
カットオフ
閾値 | 真陽性数 | 偽陰性数 | 偽陽性数 | 真陰性数 |
真陽性
割合 |
偽陰性
割合 |
偽陽性
割合 |
真陰性 割合 |
|---|---|---|---|---|---|---|---|---|
| $0.88$ | $0$ | $8$ | $0$ | $8$ | $0$ | $1$ | $0$ | $1$ |
| $0.87$ | $1$ | $7$ | $0$ | $8$ | $0.125$ | $0.875$ | $0$ | $1$ |
| $0.79$ | $2$ | $6$ | $0$ | $8$ | $0.25$ | $0.75$ | $0$ | $1$ |
| $0.73$ | $2$ | $6$ | $1$ | $7$ | $0.25$ | $0.75$ | $0.125$ | $0.875$ |
| $0.68$ | $2$ | $6$ | $2$ | $6$ | $0.25$ | $0.75$ | $0.25$ | $0.75$ |
| $0.66$ | $3$ | $5$ | $2$ | $6$ | $0.375$ | $0.625$ | $0.25$ | $0.75$ |
| $0.61$ | $4$ | $4$ | $2$ | $6$ | $0.5$ | $0.5$ | $0.25$ | $0.75$ |
| $0.57$ | $4$ | $4$ | $3$ | $5$ | $0.5$ | $0.5$ | $0.375$ | $0.625$ |
| $0.51$ | $5$ | $3$ | $3$ | $5$ | $0.625$ | $0.375$ | $0.375$ | $0.625$ |
| $0.43$ | $6$ | $2$ | $3$ | $5$ | $0.75$ | $0.25$ | $0.375$ | $0.625$ |
| $0.38$ | $7$ | $1$ | $3$ | $5$ | $0.875$ | $0.125$ | $0.375$ | $0.625$ |
| $0.35$ | $8$ | $0$ | $3$ | $5$ | $1$ | $0$ | $0.375$ | $0.625$ |
| $0.31$ | $8$ | $0$ | $4$ | $4$ | $1$ | $0$ | $0.5$ | $0.5$ |
| $0.30$ | $8$ | $0$ | $5$ | $3$ | $1$ | $0$ | $0.625$ | $0.375$ |
| $0.28$ | $8$ | $0$ | $6$ | $2$ | $1$ | $0$ | $0.75$ | $0.25$ |
| $0.27$ | $8$ | $0$ | $7$ | $1$ | $1$ | $0$ | $0.875$ | $0.125$ |
| $0.24$ | $8$ | $0$ | $8$ | $0$ | $1$ | $0$ | $1$ | $0$ |
これをもとに、ROC曲線を描くと以下のようになる。
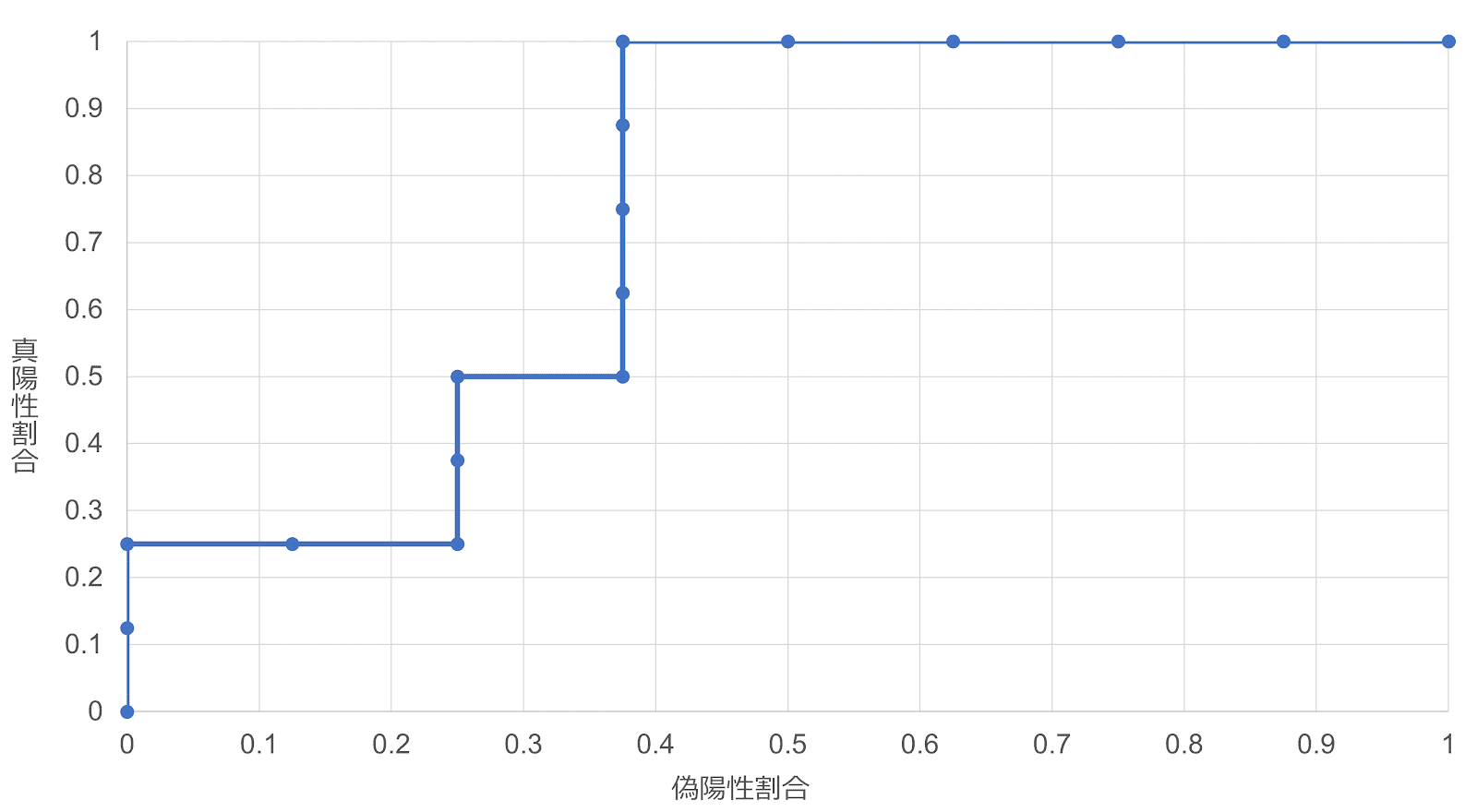
〔3〕最良のカットオフ値の選択
真陽性率と偽陽性率の差を最大にするには、真陽性率はなるべく大きな値、偽陽性率はなるべく小さい値である必要がある。この点を考慮すると、 \begin{align} \mathrm{TP}-\mathrm{FP}=1-0.375 \end{align} のときに差が最大になることが分かる。 このときのカットオフ値は、 \begin{align} X=0.35 \end{align} つまり、疾病に罹患している人の中で予測値が最小である被験者番号11以上の値をカットオフ値にするとよい(この問題の場合、この人よりも小さい予測値の人は、すべて罹患していない)。 $\blacksquare$



0 件のコメント:
コメントを投稿