医学研究における生存時間データは、新薬と標準薬の生存時間の違いなどを比較する文脈で扱われることがほとんどです。この目的のためには、生存関数の比較が必要となりますが、そのための代表的な手法にログランク検定や一般化ウィルコクソン検定などの手法があります。本稿では、そうした手法の解説をしています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
- 特に断りがない限り、打ち切りは、「情報のない右側打ち切り」のことを指します。
生存時間データの比較
医学研究では、生存時間データは、例えば「あるがんに対する新薬と標準薬の生存時間の違い」など、生存時間を比較する文脈で採取されることがよくあります。そうした場合、標準的には、まずカプラン・マイヤー法などによって生存関数の推定を行い、生存曲線の形状や、各時点の累積生存率、生存時間中央値などを確認します。それでは、生存時間の定量的な比較はどのように行えばよいのでしょうか。
生存時間データの比較法:打ち切りがない場合
まず、最も理想的な「打ち切りがない場合」には、生存時間の平均、中央値、標準偏差、さまざまなパーセント点における推定値や信頼区間などの記述統制量が利用可能なため、そうした統計量による比較が可能です。最も単純な比較方法としては、例えば介入群と非介入群の「平均生存時間の差」の信頼区間の算出や検定を行うことができます。
用いる手法としては、一般的に生存時間の分布は不明であり、歪みがあることが多いので、母集団分布に正規分布を仮定するZ検定やt検定などの手法よりも、ノンパラメトリックなウィルコクソンの順位和検定を用いることになります。
生存時間データの比較法:打ち切りがある場合
ただ、実際は打ち切りデータが含まれる場合がほとんどなので、一般的には平均生存時間などの統計量を算出することができず、単純な指標の群間比較を行うことができません。そのため、別の方法で比較を行う必要があります。
打ち切りがある場合の最も単純な比較方法は、ある時点での累積生存率の比較です。例えば、がん研究においては、5年生存率などの指標がよく用いられます。この考え方では、まず、カプラン・マイヤー法などによって、各群の生存関数を推定し、グリーンウッドの公式などで各時点における生存関数の標準誤差を算出します。そして、任意の時点 $t$ におけるカプラン・マイヤー推定量が漸近的に正規分布 \begin{gather} {\hat{S}}_j \left(t\right) \sim \mathrm{N} \left[S_j \left(t\right),V \left\{{\hat{S}}_j \left(t\right)\right\}\right] \end{gather} に従うことを利用し、 母比率の差の検定の要領で、比較を行います。例えば、介入群を $j=1$、非介入群を $j=0$ として、それぞれの累積生存率を $S_1 \left(t\right),S_0 \left(t\right)$ とすると、検定統計量は、通常のZ検定のときと同様に、 \begin{gather} Z=\frac{ \left|{\hat{S}}_1 \left(t\right)-{\hat{S}}_0 \left(t\right)\right|}{\sqrt{V \left\{{\hat{S}}_1 \left(t\right)\right\}+V \left\{{\hat{S}}_0 \left(t\right)\right\}}} \end{gather} となり、 差の信頼区間は、 \begin{gather} \mathrm{C.I.\ }= \left[\hat{d}\pm Z_{0.5\alpha} \cdot \hat{\sigma}\right]\\ \hat{d}={\hat{S}}_1 \left(t\right)-{\hat{S}}_0 \left(t\right)\\ \hat{\sigma}=\sqrt{V \left\{{\hat{S}}_1 \left(t\right)\right\}+V \left\{{\hat{S}}_0 \left(t\right)\right\}} \end{gather} となります。
こうした累積生存率の差の検定などは、基本的な統計手法をそのまま適用できるため、比較的簡単に実行することができ、結果の解釈も比較的簡単です。ただ、これはあくまでも1点における比較なので、例えば下図のように、比較する時点ではあまり差がないけど、それ以降には差がありそうな場合、その違いを検出できなくなってしまいます。
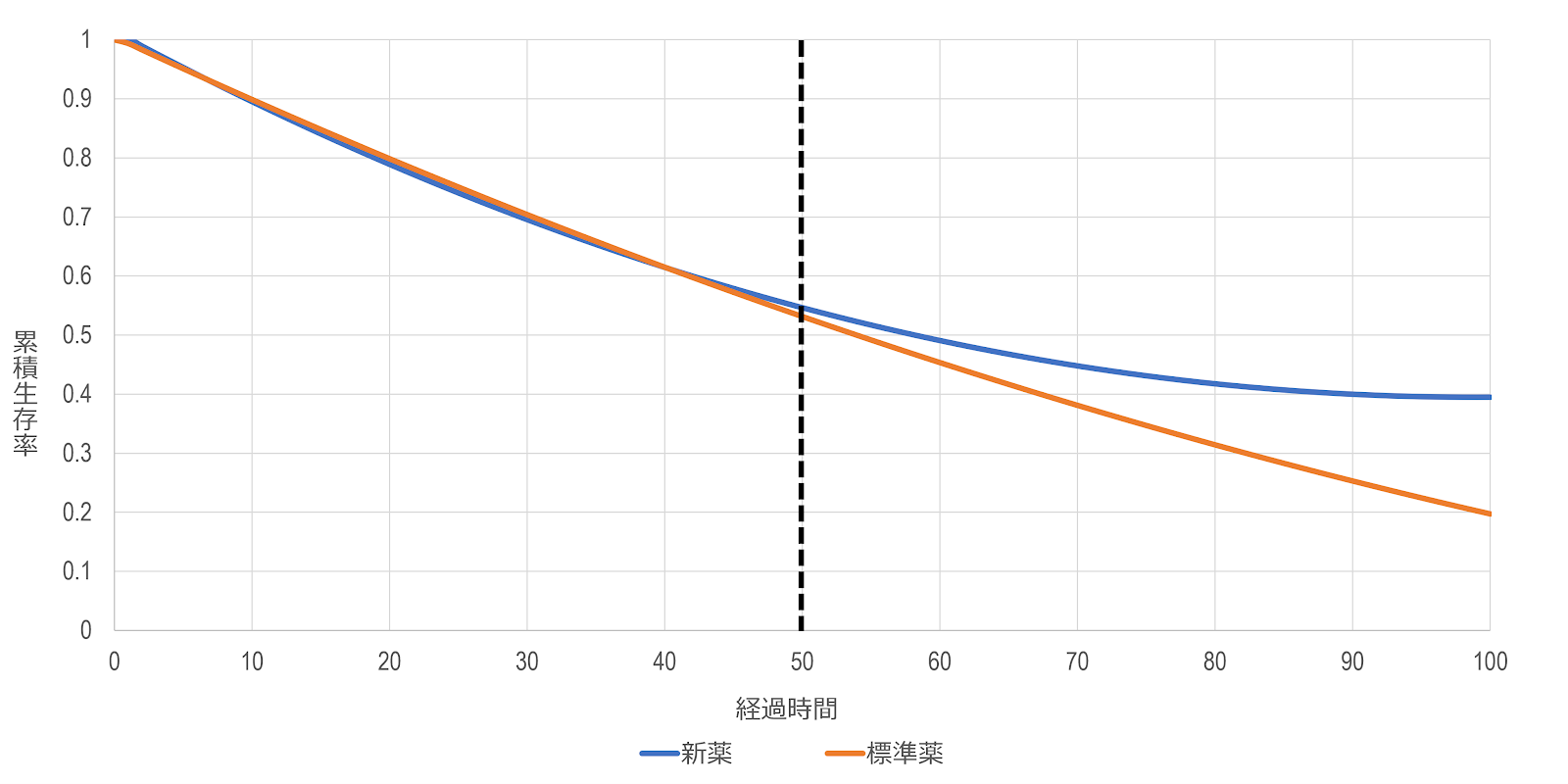
1点のみで比較するのがダメなので、複数の時点(例えば、1年、2年、3年、5年など)での比較をするという方法が思いつきますが、このやり方には検定の多重性の問題が生じ、有意水準を事前に設定した水準に保てなくなるので、不適切な方法とされています。また、例えば、「いくつかの時点で曲線が有意に異なり、他の時点では有意でない」という場合、その解釈が難しくなります。こうしたことがあるので、生存曲線を一度に、全体的に比較する方法が必要となります。
生存曲線の差の検定
検定の手順
生存曲線を全体的に比較する方法には、ログランク検定や一般化ウィルコクソン検定などの検定があります。これらの手法は、独立性の$\chi^2$検定やフィッシャーの直接法、それらを拡張したマンテル・ヘンツェル検定の応用と考えることができます。
検定仮説
すなわち、層別解析の文脈におけるマンテル・ヘンツェル検定が、$K$ 個の表に共通オッズ比が存在すると仮定し、 \begin{align} H_0:\varphi_k=1\Leftrightarrow\forall\pi_{1k}=\pi_{0k}\\ H_1:\varphi_k=\varphi \left( \neq 1\right)\Leftrightarrow\pi_{1k} \neq \pi_{0k} \end{align} を検定したとの同様に、 生存関数の均一性検定は、「2群の生存関数は同じものである」、すなわち、帰無仮説と対立仮説をそれぞれ \begin{align} H_0:S_1 \left(t\right)=S_0 \left(t\right) \quad H_1:S_1 \left(t\right) \neq S_0 \left(t\right) \end{align} として検定を行います。 なお、この検定仮説は、生存関数とハザード関数の関係から、「すべての時点におけるハザード関数が等しい」 \begin{align} H_0:h_1 \left(t\right)=h_0 \left(t\right) \quad H_1:h_1 \left(t\right) \neq h_0 \left(t\right) \end{align} という表現と同義になります。
分割表の形式
具体的な手順としては、一般的に全部で $j=1,2, \cdots ,J$ 個の群があり、それらの群全体で $i=1,2, \cdots ,I$ 個イベントが発生したとき、イベント発生時点 $t_i$ ごとに、以下のような分割表を作っていきます。ここでは、最も標準的な $J=2$ の場合を考え、介入群を $j=1$、非介入群を $j=0$ とし、時点 $t_i$ における各群のリスク集合の大きさをそれぞれ $n_{i1},n_{i0}$、各群でのイベント発生数をそれぞれ $d_{i1},d_{i0}$、リスク集合の総和を $n_i$、総イベント発生数を $d_i$ とします。
| 介入群 | 非介入群 | 合計 | |
|---|---|---|---|
| 発生数 | $d_{i1}$ | $d_{i0}$ | $d_i$ |
| 非発生数 | $n_{i1}-d_{i1}$ | $n_{i0}-d_{i0}$ | $n_i-d_i$ |
| リスク集合の 大きさ | $n_{i1}$ | $n_{i0}$ | $n_i$ |
| $t$ | $i$ | $n_{i1}$ | $d_{i1}$ | $w_{i1}$ | $n_{i0}$ | $d_{i0}$ | $w_{i0}$ |
|---|---|---|---|---|---|---|---|
| $6$ | $1$ | $5$ | $0$ | $0$ | $4$ | $1$ | $0$ |
| $14$ | $2$ | $5$ | $1$ | $0$ | $3$ | $0$ | $0$ |
| $44$ | $3$ | $4$ | $1$ | $1$ | $3$ | $0$ | $1$ |
| $98$ | $4$ | $2$ | $1$ | $0$ | $2$ | $1$ | $0$ |
| $104$ | $5$ | $1$ | $1$ | $0$ | $1$ | $0$ | $0$ |
| $114$ | $6$ | $0$ | $0$ | $0$ | $1$ | $1$ | $0$ |
続いて、イベント発生時点ごとに、分割表を作り、期待イベント数やスコア、スコアの分散を算出していきます。例えば、時点 $t_1$ については、以下のようになります。
| 介入群 | 非介入群 | 合計 | |
|---|---|---|---|
| 発生数 | $0$ | $1$ | $1$ |
| 非発生数 | $5$ | $3$ | $8$ |
| リスク集合の 大きさ | $5$ | $4$ | $9$ |
\begin{gather} e_{11}=1 \cdot \frac{5}{9}=\frac{5}{9}\\ e_{10}=1 \cdot \frac{4}{9}=\frac{4}{9} \end{gather} \begin{gather} u_{11}=w_1 \left(0-\frac{5}{9}\right)=-\frac{5}{9}w_1\\ u_{10}=w_1 \left(1-\frac{4}{9}\right)=\frac{5}{9}w_1 \end{gather} \begin{align} V \left(u_{11}\right)&=w_1^2 \cdot \frac{5 \cdot 4 \cdot 1 \left(9-1\right)}{9^2 \left(9-1\right)}=\frac{20}{81}w_1^2 \end{align}
また、打ち切りがある時点 $t_3$($t=44$、およびそれに続く $t=89$)については、カプラン・マイヤー法の基本ルール通り、打ち切り例は、分割表を作る時点では、リスク集合に含め、諸々の計算をした後に、リスク集合から除外します。そのため、以下のようになります。
| 介入群 | 非介入群 | 合計 | |
|---|---|---|---|
| 発生数 | $1$ | $0$ | $1$ |
| 非発生数 | $3$ | $3$ | $6$ |
| リスク集合の 大きさ | $4$ | $3$ | $7$ |
\begin{gather} e_{31}=1 \cdot \frac{4}{7}=\frac{4}{7}\\ e_{30}=1 \cdot \frac{3}{7}=\frac{3}{7} \end{gather} \begin{gather} u_{31}=w_3 \left(1-\frac{4}{7}\right)=\frac{3}{7}w_3\\ u_{30}=w_3 \left(0-\frac{3}{7}\right)=-\frac{3}{7}w_3 \end{gather} \begin{align} V \left(u_{31}\right)&=w_3^2 \cdot \frac{4 \cdot 3 \cdot 1 \left(7-1\right)}{7^2 \left(7-1\right)}=\frac{12}{49}w_3^2 \end{align} \begin{gather} n_{41}=4-1-1=2\\ n_{40}=3-0-1=2 \end{gather}
こうした作業をすべてのイベント発生時点で行うと、以下のように整理することができます。なお、$w_i \left(LR\right)$ はログランク検定による重み、$w_i \left(GW\right)$ は一般化ウィルコクソン検定による重みを表しています。スコアとスコアの分散についても同様です。
| $t_i$ | $d_{i1}$ | $n_{i1}$ | $d_i$ | $n_i$ | $e_{i1}$ | $V \left(d_{i1}\right)$ | $w_i \left(LR\right)$ | $w_i \left(GW\right)$ |
|---|---|---|---|---|---|---|---|---|
| $1$ | $0$ | $5$ | $1$ | $9$ | $0.556$ | $0.247$ | $1$ | $9$ |
| $2$ | $1$ | $5$ | $1$ | $8$ | $0.625$ | $0.234$ | $1$ | $8$ |
| $3$ | $1$ | $4$ | $1$ | $7$ | $0.571$ | $0.245$ | $1$ | $7$ |
| $4$ | $1$ | $2$ | $2$ | $4$ | $1$ | $0.333$ | $1$ | $4$ |
| $5$ | $1$ | $1$ | $1$ | $2$ | $0.5$ | $0.250$ | $1$ | $2$ |
| $6$ | $0$ | $0$ | $1$ | $1$ | $0$ | $0$ | $1$ | $1$ |
| $t_i$ | $u_{i1} \left(LR\right)$ | $u_{i1} \left(GW\right)$ | $V_{LR} \left(u_{i1}\right)$ | $V_{GW} \left(u_{i1}\right)$ |
|---|---|---|---|---|
| $1$ | $-0.556$ | $-5$ | $0.247$ | $20$ |
| $2$ | $0.375$ | $3$ | $0.234$ | $15$ |
| $3$ | $0.429$ | $3$ | $0.245$ | $12$ |
| $4$ | $0$ | $0$ | $0.333$ | $5.333$ |
| $5$ | $0.5$ | $1$ | $0.250$ | $1$ |
| $6$ | $0$ | $0$ | $0$ | $0$ |
\begin{gather} u_1 \left(\mathrm{LR}\right)\cong0.748 \quad u_1^2 \left(\mathrm{LR}\right)\cong0.560\\ V_{\mathrm{LR}} \left(u_{i1}\right)=1.310\\ \chi_{\mathrm{LR}}^2=0.427\\ \mathrm{P}=0.513 \end{gather} \begin{gather} u_1 \left(\mathrm{GW}\right)=2 \quad u_1^2 \left(\mathrm{GW}\right)=4\\ V_{\mathrm{GW}} \left(u_{i1}\right)=53.33\\ \chi_{\mathrm{GW}}^2=0.075\\ \mathrm{P}=0.784 \end{gather}
このデータでの検定結果は、どちらの方法でも有意水準5%で有意差なし、すなわち、「介入群と非介入群の生存関数は異なっているとは言えない」という結果になりました。ただ、この結果は、サンプルサイズの小ささに起因するところが大きく、漸近性の仮定が成り立たないと思われることから、有意性は参考程度のものとなります。
その他の検定法
Peto-Peto流のログランク検定
ログランク検定は、分散の計算が少し複雑です。そこで手計算でも計算できるように、簡便化したのが、Peto-Peto流のログランク検定$^\mathrm{(4,9)}$です。Peto-Peto流のログランク検定の検定統計量は \begin{gather} \chi_{\mathrm{PPLR}}^2=\sum_{j=1}^{J}\frac{ \left(d_j-e_j\right)^2}{e_j}=\sum_{j=1}^{J}\frac{ \left\{\sum_{i=1}^{I} \left(d_{ij}-e_{ij}\right)\right\}^2}{\sum_{i=1}^{I}e_{ij}} \end{gather} となります。 例えば、$J=0,1$ の2群の場合、 \begin{gather} \chi_{\mathrm{PPLR}}^2=\frac{ \left(D_1-E_1\right)^2}{E_1}+\frac{ \left(D_0-E_0\right)^2}{E_0}\\ E_j=\sum_{i=1}^{I}e_{ij} \quad D_j=\sum_{i=1}^{I}d_{ij} \end{gather} となります。
この方法では、$d_{ij},e_{ij}$ さえわかれば検定統計量を構成でき、分散については新たに計算する必要がなりません。また適合度の $\chi^2$検定と同様に、観測値と期待値の差の2乗を期待値で割ったわかりやすい形をしています。ただし、Peto-Peto流のログランク検定は少し保守的であり、ログランク検定と比べて、有意になりにくいことが知られています。
Peto-Prentice 流の一般化ウィルコクソン検定
Peto-Peto(1972)$^\mathrm{(4)}$とPrentice(1978)$^\mathrm{(10)}$は、標本を併合した生存時間に依存する重みを提案しました。重みは、カプラン・マイヤー推定量を修正したものであり、イベント時間を観測する以前の情報で定義されます。タイデータがある場合($d_i \geq 1$)にも一般化された修正カプラン・マイヤー推定量は、 \begin{gather} \hat{S} \left(t\right)=\prod_{t_i \le t}\frac{n_i+1-d_i}{n_i+1} \end{gather} このとき、各時点の重みは、 \begin{gather} w_i=\hat{S} \left(t_i\right) \end{gather} 修正Peto-Prentice検定は、重み \begin{gather} w_i=\hat{S} \left(t_{i-1}\right)\times\frac{n_i}{n_i+1} \end{gather} を用います。
重みを全時点で1としたログランク検定は、サンプルサイズが小さくなる後半の分散が大きくなるため、後半のデータに大きな重みがつき、重みをその時点のリスク集合全体の大きさとした一般化ウィルコクソン検定は、早期のイベントの影響が大きくなります。これは、特に打ち切りが非常に多く、ある時点のリスク集合の大きさが小さくなってしまう場合に、少数の時点の検定統計量に対する寄与が極端に高くなってしまうという問題の原因となってしまうため、そうした問題に対する改善策として考案されました。
注意事項
生存関数の違いの検定では、これまでに示したように死亡までの時間の順位情報のみを用いて、死亡時点ごとに分割表を作ります。1番最初に死亡すれば、1日目であろうが、1年目であろうが、同じ扱いをします。この意味で、生存時間に関する情報を完全に使っているわけではなく、情報のロスがあります。
一般化ウィルコクソン検定とログランク検定の違いは、重みの付け方の違いからも明らかなように、一般化ウィルコクソン検定が相対的に試験の初期に起きた死亡を重く評価するのに対し、ログランク検定は後期に起きた死亡を重く評価します。ただし、一般化ウィルコクソン検定とログランク検定のいずれも、どちらかの群で生存関数が一様に高いという対立仮説を想定しているため、生存関数が交差するような場面での検出力は低くなることに注意が必要です。
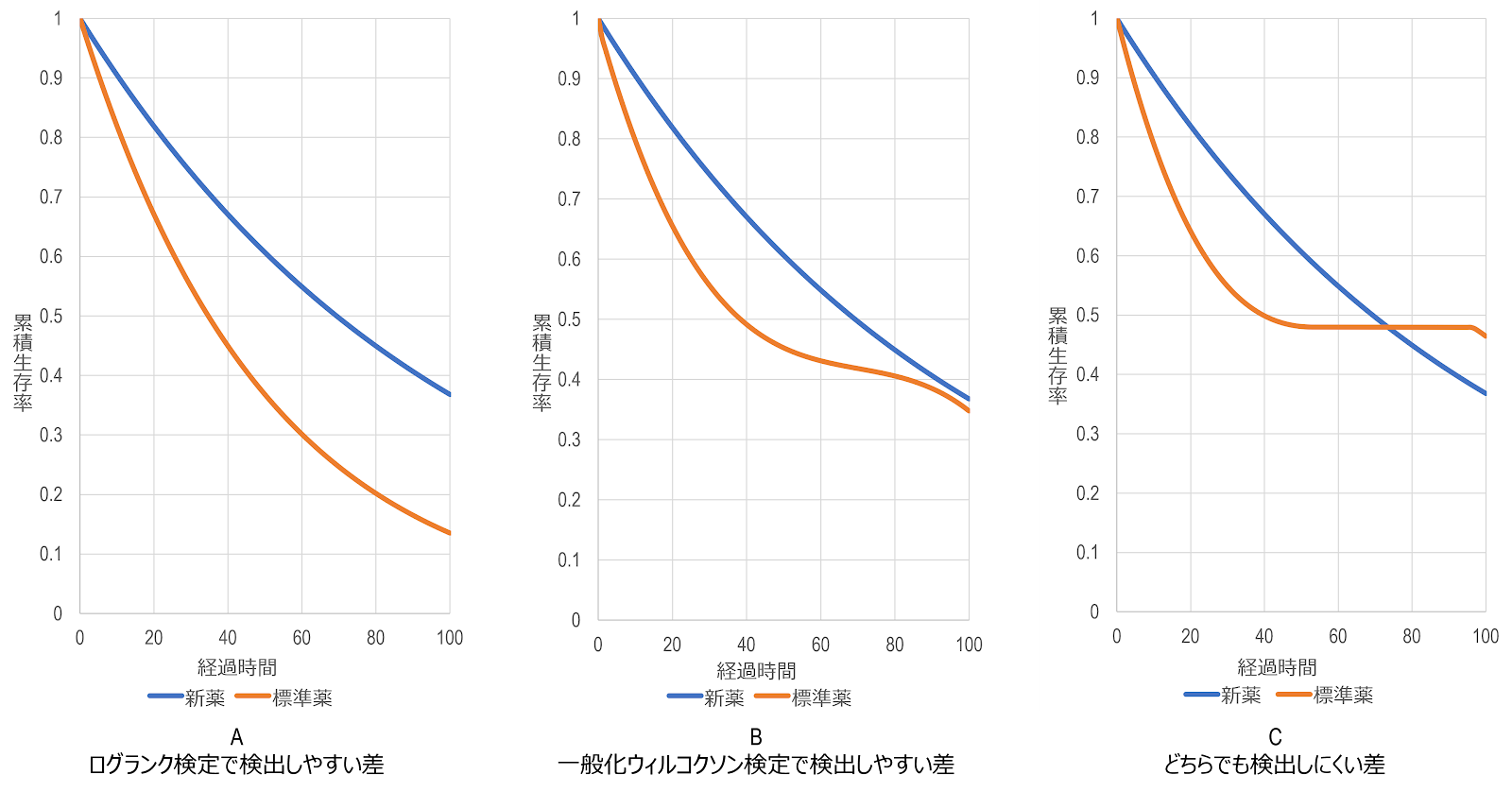
ハザード比の信頼区間
一般的な統計的推論の方法と同様、生存曲線の差についても、検定に対応した、定量的な信頼区間を算出することができます。ただ、生存曲線の差については、全体を通しての生存関数(累積生存率)ではなく、全体を通してのハザード $h \left(t\right)$ を考え、特に相対リスクとしてのハザード比 hazard ratio \begin{gather} \mathrm{HR}=\frac{h_1 \left(t\right)}{h_0 \left(t\right)} \end{gather} を指標とします。
ハザード比を計算することで、「リスク因子があるとイベント発生確率が単位時間あたり何倍になるのか」あるいは「予防対策を行うとイベント発生を単位時間当たり何分の1に減らせるのか」といった具体的な効果を推定し、表現することができます。入院期間や特定の医療器具の使用期間など、時間の影響を受けるイペントの発生頻度を要因の有無で比較評価する場合、時間的な影響(曝露の程度)を調整できるこの視標を用いることで、バイアスの混入を回避して評価することができます。
生存関数の均一性の検定に対応したハザード比は、群 $j$ における全期間を通しての観測イベント総数を \begin{gather} D_j=\sum_{i=1}^{I}d_{ij} \end{gather} 全期間を通しての期待イベント総数を \begin{gather} E_j=\sum_{i=1}^{I}e_{ij} \end{gather} として、 \begin{gather} \mathrm{HR}=\frac{\frac{D_1}{E_1}}{\frac{D_0}{E_0}}=\frac{E_0D_1}{E_1D_0} \end{gather} で定義されます。 推定は対数ハザード比 $\log{\mathrm{HR}}$ とスコアの分散 $V \left(u_1\right)$ を用いて、 \begin{gather} \log{\mathrm{\widehat{HR}}}=\frac{D_1-E_1}{V \left(u_1\right)} \end{gather} で推定することができます。 これは、生存関数の均一性の検定統計量 $\chi^2$ と同じ量であり、この推定値の標準誤差は、近似的に \begin{gather} \mathrm{S.E.} \left(\log{\mathrm{\widehat{HR}}}\right)=\frac{1}{\sqrt{V \left(u_1\right)}} \end{gather} となるため、 対数ハザード比の $100 \left(1-\alpha\right)\\%$ 信頼区間は、 \begin{gather} 100 \left(1-\alpha\right)\%\ \mathrm{C.I.}: \left[\log{\mathrm{\widehat{HR}}}\pm Z_{0.5\alpha} \cdot \mathrm{S.E.} \left(\log{\mathrm{\widehat{HR}}}\right)\right]\\ \end{gather} で与えられます$^\mathrm{(11)}$。
参考文献
- 大橋 靖雄, 浜田 知久馬 著. 生存時間解析:SASによる生物統計. 東京大学出版会, 1995, p.35-50
- 前谷 俊三 著. 臨床生存分析:生存データと予後因子の解析. 南江堂, 1996, p.38-51
- ダグラス・アルトマン 著, 木船 義久, 佐久間 昭 訳. 医学研究における実用統計学. サイエンティスト社, 1999, p.297-300, p.304-306
- デーヴィッド・マシューズ, ヴァーノン・フェアウェル 著, 宮原 英夫, 折笠 秀樹 監訳, 小田 英世, 手良向 聡, 森田 智視 訳. 実践医学統計学. 朝倉書店, 2005, p.69-76
- 中村 剛 著. Cox比例ハザードモデル. 朝倉書店, 2001, p.16-21
- 浜田 知久馬 著. 学会・論文発表のための統計学:統計パッケージを誤用しないために. 真興交易医書出版部, 2012, p.222-231
- デビッド・ホスマー, スタンリー・レメショウ, スーザン・メイ 著, 五所 正彦 監訳. 生存時間解析入門. 東京大学出版会, 2014, p.47-62
- ジョン・ラチン 著, 宮岡 悦良 監訳, 遠藤 輝, 黒沢 健, 下川 朝有, 寒水 孝司 訳. 医薬データのための統計解析. 共立出版, 2020, p.469-475, p.481-489
- Clark, T.G., Bradburn, M.J., Love, S.B. et al.. Survival analysis part I: basic concepts and first analyses. Br J Cancer. 2003, 89(2), p.232-238, doi: 10.1038/sj.bjc.6601118
- 藤田 烈. 疫学・統計解析シリーズ:生存時間解析結果を読み解くための基礎知識. 日本環境感染学会誌. 2014, 29(5), p.313-323, doi: 10.4058/jsei.29.313
引用文献
- Fleming, T.R. & Harrington, D.P.. Counting Processes and Survival Analysis. Wiley & Sons, Inc., 2005, 454p.
- Andersen, P.K., Borgan, Ørnulf, Gill, R.D. et al.. Statistical Models Based on Counting Processes. Springer Verlag, 1993, 784p.
- Mantel, N. Evaluation of survival data and two new rank order statistics arising in its consideration. Cancer Chemother Rep. 1966, 50(3), p.163-170.
- Peto, R. & Peto, J.. Asymptotically efficient rank invariant test procedure. Journal of the Royal Statistical Society. 1972, Series A135, p.185-207, doi: 10.2307/2344317
- Gehan, E.A.. A generalized Wilcoxon test for comparing arbitrarily singly-censored samples. Biometrika. 1965, 52, p.203-223, doi: 10.2307/2333825
- Breslow, N.E.. A Generalized Kruskal-Wallis Test for Comparing K Samples Subject to Unequal Patterns of Censorship. Biometrika. 1970, 57(3), p.579-594, doi: 10.1093/biomet/57.3.579
- Tarone, R.E. & Ware, J.. On Distribution-Free Tests for Equality of Survival Distributions. Biometrika. 1977, 64(1), p.156-160, doi: 10.1093/biomet/64.1.156
- デビッド・ホスマー, スタンリー・レメショウ, スーザン・メイ 著, 五所 正彦 監訳. 生存時間解析入門. 東京大学出版会, 2014, p.53-54
- Peto, R., Pike,M.C., Armitage, P. et al.. Design and analysis of randomized clinical trials requiring prolonged observation of each patient. II. analysis and examples. British journal of cancer. 1977, 35(1), p.1-39, doi: 10.1038/bjc.1977.1
- Prentice, R.L.. Linear rank tests with right-censored data. Biometrika. 1978, 65, p.167-179, doi: 10.1093/biomet/65.1.167
- Simon, R. Confidence intervals for reporting results of clinical trials. Academia and Clinic. 1986, 105(3), p.429-435, doi: 10.7326/0003-4819-105-3-429
関連記事
あるノマドの知の旅路~数学・統計学への道



0 件のコメント:
コメントを投稿