医学研究では、予後予測や交絡因子の調整のために回帰分析が用いられることがありますが、生存時間データの場合、コックスの比例ハザードモデルという回帰モデルが使われます。本稿では、比例ハザードモデルの定義や比例ハザード性の意味や検証方法、回帰係数の推定法(部分尤度法)などについて解説しています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
- 特に断りがない限り、打ち切りは、「情報のない右側打ち切り」のことを指します。
生存時間データに対する回帰分析
医学・疫学研究は、その成果を根拠として、さまざまな背景をもった個人ひとりひとりに対する最適な医療を提供することを最終的な目的としています。そうした医学・疫学研究の研究テーマのひとつとしての①予後予測、あるいは、②さまざまな共変量が疾病に対して単独で与える影響の評価(交絡因子の調整)などを目的として、重回帰分析やロジスティック回帰分析などの回帰分析が行われています。そうした背景を鑑みると、生存時間データに対しても、同様に予後予測や交絡因子の調整のために回帰モデルの構築ができそうな気がしますが、結論から言えば、生存時間データに対して回帰モデルを構築する場合、打ち切りデータの問題などがあるために、少々工夫した特別な方法が必要となります。
生存時間の予測
ではまず、生存時間の予測という文脈での回帰モデルについて考えましょう。本質的に生存時間 $T$ は、連続変数であると考えられるので、個人がもつ $p$ 個の共変量と $p+1$ 個の回帰係数を \begin{gather} \boldsymbol{X}= \left\{\begin{matrix}X_1\\X_2\\\vdots\\X_p\\\end{matrix}\right\} \quad \boldsymbol{\theta}= \left\{\begin{matrix}\alpha\\\boldsymbol{\beta}\\\end{matrix}\right\} \quad \boldsymbol{\beta}= \left\{\begin{matrix}\beta_1\\\beta_2\\\vdots\\\beta_p\\\end{matrix}\right\} \end{gather} として、 通常の線形重回帰によるモデル \begin{gather} T=\alpha+\boldsymbol{X}^\boldsymbol{T}\boldsymbol{\beta}=\alpha+\beta_1X_1+ \cdots +\beta_pX_p \end{gather} が考えられます。 すなわち、$i$ 番目の個人の共変量の値を \begin{gather} \boldsymbol{x}_\boldsymbol{i}= \left\{\begin{matrix}x_{i1}\\x_{i2}\\\vdots\\x_{ip}\\\end{matrix}\right\} \end{gather} とするとき \begin{gather} T_i=\alpha+\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}=\alpha+\beta_1x_{i1}+ \cdots +\beta_px_{ip} \end{gather} とするモデルです。 共変量の種類には、性別や遺伝子型、治療法などの名義尺度、病気の進行状況(ステージ)などの順序尺度、年齢や血圧値などの比例尺度など、さまざまなものがあります。
この回帰式を予測のために使うためには、実際に得られたデータから偏回帰係数を推定する必要があります。もしすべての被験者にイベントが起こるまで観察できたとき、つまり、打ち切りがない場合は、そのデータによって、推定を行うことができます。しかし、通常、生存時間データには、打ち切りがつきものなので、単純に重回帰分析の手法を適用することができません。打ち切りデータを除外して推定を行うこともできますが、データを捨てる分だけ研究の効率が低下しますし、バイアスがかかった結果が得られてしまう可能性もあるため、少し工夫したやり方が必要となります。
加速死亡時間モデル
そうした問題に対応した手法が、加速死亡時間モデル accelerated failure time model: AFT$^\mathrm{(1,2,3)}$ と呼ばれる回帰モデルです。この回帰モデルは、生存時間の分布に特定の分布を仮定するパラメトリックな回帰モデルであり、$\varepsilon$ を誤差項として、 \begin{gather} T=e^{\alpha+\beta_1X_1+ \cdots +\beta_pX_p}\times\varepsilon\tag{1}\\ \Leftrightarrow\log{T}=\alpha+\beta_1X_1+ \cdots +\beta_pX_p+\log{\varepsilon}\tag{2} \end{gather} とするモデルです。 加速死亡時間モデルは、回帰係数を推定する際に、打ち切りの情報を盛り込むことができるので、得られたデータを無駄なく活用することができ、関心の対象となっている生存時間を直接的に算出できるので、非常に分かりやすいモデルです$^\mathrm{(4)}$。
ただ、加速死亡時間モデルは、生存時間が対数正規分布やワイブル分布、対数ロジスティック分布、一般化ガンマ分布などの分布に従っていることを仮定するため、その仮定が満たされていない条件下では妥当とは言えません。医学研究の文脈では、生存時間の分布は疾患によってさまざまで、一般的にはデータから母集団の分布を特定することができないため、分かりやすくて魅力的な方法ではありますが、汎用性に難がある方法とされています。
共変量の影響評価(交絡因子の調整)
生存時間分析を行う場合、カプラン・マイヤー法などによって生存関数を推定し、ログランク検定や一般化ウィルコクソン検定などの手法で検定を行うという流れが標準的な分析方法です。こうした方法では、例えば、あるがんに対する生存時間を調べる場合、新薬投与群と標準薬投与群の2群に分け、それぞれの生存曲線を描き、検定で生存曲線に差があるかどうかを調べます。これは、いいかえると、「新薬投与の有無」という1つの共変量の効果について検証しているので、本質的に単変量解析としての分析ということになります。
しかし、通常の単変量解析と同様、生存時間分析の場合も、ある因子の影響によって真実とは異なる結果が出てしまう、交絡の問題が発生することがあります。例えば、ある疾病に対する治療法Aと治療法Bによる生存時間の比較を行う際、治療法Aのカプラン・マイヤー曲線が終始上にあって、ログランク検定でも治療法Aの生存時間が有意にBよりも長いという結果が得られたら、治療法Aの方が優れていることになります。しかし例えば、治療法Bの対象者が高齢で重症な患者ばかりであったら、それは治療法Bが劣っているからなのか、それとも、そうした生存時間を縮める要因の影響が大きく出ていただけなのか、判断できません。この場合、治療法Aの優位性を立証するためには、そうした共変量の影響を取り除いたうえでもなお、治療法Aの生存時間が長いことを示さなければなりません。
そうした交絡因子の調整の方法には、通常の分割表の分析と同様、生存時間分析における層別解析の手法である層別ログランク検定と生存時間データに対する回帰分析の2種類の方法があります。回帰モデルの構築については、先に出た加速死亡時間モデルのパラメトリックなモデルを仮定することもできますが、そうした条件を緩めた方法が次で紹介するコックスの比例ハザードモデルです。
比例ハザードモデル
比例ハザードモデル proportlonal hazards model とは、Cox(1972)$^\mathrm{(5)}$ によって提唱された方法で、ある共変量ベクトル $\boldsymbol{x}$ をもつ個人のハザード関数を $h \left(t\middle|\boldsymbol{x}\right)$ とするとき、 \begin{align} h \left(t\middle|\boldsymbol{x}\right)&=h_0 \left(t\right) \cdot r \left(\boldsymbol{x},\boldsymbol{\beta}\right)\\ &=h_0 \left(t\right) \cdot e^{\boldsymbol{x}^\boldsymbol{T}\boldsymbol{\beta}}\\ &=h_0 \left(t\right) \cdot e^{\alpha+\beta_1x_1+ \cdots +\beta_px_p}\tag{3} \end{align} とするモデルです。
この式にある $h_0 \left(t\right)$ は、回帰係数がすべて $\boldsymbol{\beta}=\boldsymbol{0}\Leftrightarrow\alpha=\beta_1= \cdots =\beta_p=0$ の場合のハザードを表し、ベースライン・ハザード関数 baseline hazard function や基本ハザード関数 underlying hazard function と呼ばれます。ベースライン・ハザードは、経過時間 $t$ の関数(=時間経過によって増減する値)で、ハザードに対する経過時間の影響を表す部分です。また、共変量の値の組み合わせによらない、対象とする集団に共通した値という意味もあります。
いっぽう、$r \left(\boldsymbol{x},\boldsymbol{\beta}\right)$ の部分は、ハザードに対する共変量の影響を表す部分であり、具体的な値 $\boldsymbol{x}$ が与えられた条件下では、 \begin{gather} e^{\alpha+\beta_1x_1+ \cdots +\beta_px_p}=c \end{gather} となり、 基本的に定数として扱います。つまりこの部分は、経過時間によらない比例定数を表しており、回帰係数 $\boldsymbol{\beta}$ を推定することでその影響度合いを知ることができます。例えば、ハザードを50%上昇させる(1.5倍にする)因子が2つ重なると、 \begin{gather} e^{\beta_1x_1} \cdot e^{\beta_2x_2}=1.5 \cdot 1.5=2.25 \end{gather} となり、 このモデルの下では、ハザードが2.25倍になります。
このモデルは、ある個人のハザード関数が「経過時間に依存する部分(ベースライン・ハザード)」と「経過時間に依存しない部分」の積で表されています。このようなモデルを乗法モデル multiplicative model といい、共変量の影響がベースライン・ハザードに $c$ という比例定数のかたちで影響するため、「比例ハザードモデル」と呼ばれています。
比例ハザードモデルは、評価の対象としている指標が生存時間 $T$ そのものではなく、経過時間の関数であるハザード関数 $h \left(t\right)$ としているため、やや回り道をした評価方法です。ただ、ハザード関数と生存関数の関係を用いると、もう少し分かりやすい生存関数や生存曲線による評価が可能になりますし、後に見るように、交絡因子の調整という文脈で見た場合、ある共変量が単独でハザードに与える影響を定量的に把握することもできます。こうした意味において、比例ハザードモデルは、個々の共変量が生存時間に与える影響の評価という文脈で解釈すると分かりやすくなります。
比例ハザードモデルに必要な仮定:比例ハザード性
加速死亡時間モデルには、「生存時間が特定のパラメトリックな分布に従う」という仮定が必要でしたが、比例ハザードモデルにも1つだけ必要な仮定があります。それが、比例ハザード性の仮定です。
比例ハザード性の仮定 proportional hazard assumption とは、異なる共変量をもつ2人の個人間のハザード比が時点によらず一定であるという仮定のことです。例えば、AさんとBさんの共変量の値をそれぞれ、 \begin{gather} \boldsymbol{x}_\boldsymbol{A}= \left\{\begin{matrix}x_{A1}\\x_{A2}\\\vdots\\x_{Ap}\\\end{matrix}\right\} \quad \boldsymbol{x}_\boldsymbol{B}= \left\{\begin{matrix}x_{B1}\\x_{B2}\\\vdots\\x_{Bp}\\\end{matrix}\right\} \end{gather} とするとき、 比例ハザードモデルにおけるハザード関数は、それぞれ \begin{gather} h \left(t\middle|\boldsymbol{x}_\boldsymbol{A}\right)=h_0 \left(t\right) \cdot e^{\alpha+\beta_1x_{A1}+ \cdots +\beta_px_{Ap}}=h_0 \left(t\right) \cdot c_A\\ h \left(t\middle|\boldsymbol{x}_\boldsymbol{B}\right)=h_0 \left(t\right) \cdot e^{\alpha+\beta_1x_{B1}+ \cdots +\beta_px_{Bp}}=h_0 \left(t\right) \cdot c_B \end{gather} となります。 このとき、例えば、Bに対するAのハザード比は、ベースライン・ハザードが相殺されるので、 \begin{gather} \frac{h \left(t\middle|\boldsymbol{x}_\boldsymbol{A}\right)}{h \left(t\middle|\boldsymbol{x}_\boldsymbol{B}\right)}=\frac{h_0 \left(t\right) \cdot c_A}{h_0 \left(t\right) \cdot c_B}=\frac{c_A}{c_B}=\lambda \end{gather} というように定数になります。 したがって、ある時点 $t_1$ におけるBさんのハザードが仮に \begin{gather} h \left(t_1\middle|\boldsymbol{x}_\boldsymbol{B}\right)=h_0 \left(t_1\right) \cdot c_B=1 \end{gather} ハザード比が $\lambda=2$ ならば、時点 $t_1$ におけるAさんのハザードは、 \begin{gather} h \left(t_1\middle|\boldsymbol{x}_\boldsymbol{A}\right)=h_0 \left(t_1\right) \cdot c_A=2 \end{gather} ある時点 $t_2$ におけるBさんのハザードが \begin{gather} h \left(t_2\middle|\boldsymbol{x}_\boldsymbol{B}\right)=h_0 \left(t_2\right) \cdot c_B=2 \end{gather} ならば、 \begin{gather} h \left(t_2\middle|\boldsymbol{x}_\boldsymbol{A}\right)=h_0 \left(t_2\right) \cdot c_A=4 \end{gather} というように、 それぞれのハザードの値は経過時間によって変化しても、その比は変わらないということです。
この仮定は、それなりに強い仮定であり、現実のデータで比例ハザード性が成り立つかはその都度検証する必要がありますが、逆に言えば、それは検証可能なものとも言えます。比例ハザード性の仮定さえ満たされていれば、加速死亡時間モデルのような生存時間の分布に対する仮定が必要ないため、汎用性に優れた手法として現在、定着しています。
基準生存関数
比例ハザードモデルは、生存時間 $T$ そのものではなく、その関数であるハザード関数に着目していますが、ハザードはその具体的な意味が掴みにくい部分もあるので、どうせなら、分かりやすい生存関数のかたちで表現したいところです。
この点、まず、比例ハザードモデルにハザード関数と累積ハザード関数の関係式を当てはめると、 \begin{align} H \left(t\middle|\boldsymbol{x}\right)&=\int_{0}^{t}{h \left(u\middle|\boldsymbol{x}\right)du}\\ &=\int_{0}^{t}{h_0 \left(u\right) \cdot r \left(\boldsymbol{x},\boldsymbol{\beta}\right)du}\\ &=r \left(\boldsymbol{x},\boldsymbol{\beta}\right)\int_{0}^{t}{h_0 \left(u\right)du}\\ &=H_0 \left(t\right) \cdot r \left(\boldsymbol{x},\boldsymbol{\beta}\right)\tag{4} \end{align} となりますが、 この $H_0 \left(t\right)$ を累積基準ハザード関数と呼びます。
続いて、生存関数と累積ハザード関数の関係式より、 \begin{align} S \left(t\middle|\boldsymbol{x}\right)&=e^{-H \left(t\middle|\boldsymbol{x}\right)}\\ &=e^{-H_0 \left(t\right) \cdot r \left(\boldsymbol{x},\boldsymbol{\beta}\right)}\\ &= \left\{e^{-H_0 \left(t\right)}\right\}^{r \left(\boldsymbol{x},\boldsymbol{\beta}\right)}\\ &= \left\{S_0 \left(t\right)\right\}^{r \left(\boldsymbol{x},\boldsymbol{\beta}\right)}\tag{5} \end{align} となります。 この、 \begin{gather} S_0 \left(t\right)=e^{-H_0 \left(t\right)}\tag{6} \end{gather} を基準生存関数 baseline survivat function と呼びます。
時間依存性共変量
なお厳密には、共変量には、①時間によらない共変量と②時間依存性共変量の2 種類があります。時間によらない共変量とは、「性別」や「遺伝子型」のように、時間が経っても変わらない共変量のことです。
いっぽう、時間依存性共変量 time dependent covariate、または時変共変量 time-varying covariate とは、「病気の進行状況」や「タバコの喫煙本数」、「血圧値」など時間と共に値が変化する可能性がある共変量のことを指します。
共変量が時間依存性共変量の場合、共変量の影響も時間の関数となるため、その点を考慮した方法が必要となりますが、現在の主流となっている方法では、時間依存性共変量はモデルに含まれておらず、時間によらない共変量のみを扱っているため、本稿でもそうした最も単純な場合を想定して解説を進めます。
回帰係数の意味
ロジスティック回帰モデルの場合、回帰係数は「他の共変量がすべて等しい場合、ある共変量を1単位変化させたときの対数オッズ比」を意味していました。比例ハザードモデルにおいても、同様の意味となります。例えば、共変量 $x_1$ の値が異なり、他の共変量はすべて等しい場合、すなわち、 \begin{gather} \boldsymbol{x}_\boldsymbol{A}= \left\{\begin{matrix}x_{A1}\\x_2\\\vdots\\x_p\\\end{matrix}\right\} \quad \boldsymbol{x}_\boldsymbol{B}= \left\{\begin{matrix}x_{B1}\\x_2\\\vdots\\x_p\\\end{matrix}\right\} \end{gather} とするとき、 比例ハザードモデルにおけるハザード比は、 \begin{align} \mathrm{HR}&=\frac{h \left(t\middle|\boldsymbol{x}_\boldsymbol{A}\right)}{h \left(t\middle|\boldsymbol{x}_\boldsymbol{B}\right)}\\ &=\frac{h_0 \left(t\right) \cdot e^{\alpha+\beta_1x_{A1}+ \cdots +\beta_px_p}}{h_0 \left(t\right) \cdot e^{\alpha+\beta_1x_{B1}+ \cdots +\beta_px_p}}\\ &=\frac{h_0 \left(t\right) \cdot e^{\alpha+ \cdots +\beta_px_p}}{h_0 \left(t\right) \cdot e^{\alpha+ \cdots +\beta_px_p}} \cdot \frac{e^{\beta_1x_{A1}}}{e^{\beta_1x_{B1}}}\\ &=e^{\beta_1 \left(x_{1A}-x_{1B}\right)} \end{align} 特に、例えば、「性別」のような2値変数(男性なら1、女性なら0)の場合、 \begin{gather} \mathrm{HR}=e^{\beta_1 \left(1-0\right)}=e^{\beta_1}\\ \Leftrightarrow\log{\mathrm{HR}}=\beta_1\tag{7} \end{gather} となります。 したがって、比例ハザードモデルにおける回帰係数は、他の共変量がすべて等しい場合、ある共変量を1単位変化させたときの対数ハザード比を意味します。
この関係は、ベースライン・ハザード $h_0 \left(t\right)$ の具体的な値が分からなくても、成り立つ関係であるため、ある共変量がハザード≒生存時間に与える影響を調べるうえで、非常に重要な関係であるといえます。
回帰係数の推定と検定
生存時間データの尤度関数
比例ハザードモデルにおける回帰係数の推定には、ロジスティック回帰モデルの場合と同様、最尤法が用いられます。そのため、まず尤度関数を求める必要があります。いま、$i=1,2, \cdots ,N$ の $N$ 人の生存時間データの組 $ \left(t_i,\delta_i\right)$ があるとします。一般に、ある人の生存関数、ハザード関数、死亡密度関数をそれぞれ \begin{gather} S \left(t\right) \quad h \left(t\right) \quad f \left(t\right) \end{gather} とするとき、 番号 $i$ の人のデータが得られる確率は、 \begin{gather} L_i= \left\{f \left(t_i\right)\right\}^{\delta_i} \left\{S \left(t_i\right)\right\}^{1-\delta_i}\tag{8} \end{gather} となります。 すなわち、イベントが発生した場合($\delta_i=1$)は「ちょうど $t_i$ の時点でイベントが発生する確率」なので \begin{gather} P \left(T=t_i\right)=f \left(t_i\right) \end{gather} 打ち切りの場合($\delta_i=0$)は、「$t_i$ よりも長く生存する確率」なので、 \begin{gather} P \left(t_i \le T\right)=S \left(t_i\right) \end{gather} となり、 指示関数 $\delta_i$ を上手く利用すると、式 $(8)$ の形で表されます。このことから、全体としての尤度関数は、 \begin{gather} L=\prod_{i=1}^{N}{ \left\{f \left(t_i\right)\right\}^{\delta_i} \left\{S \left(t_i\right)\right\}^{1-\delta_i}}\tag{9} \end{gather} で与えられます。 また、生存関数、ハザード関数、死亡密度関数の関係式 $f \left(t\right)=h \left(t\right) \cdot S \left(t\right)$ を用いると、 \begin{align} L&=\prod_{i=1}^{N}{ \left\{h \left(t_i\right) \cdot S \left(t_i\right)\right\}^{\delta_i} \left\{S \left(t_i\right)\right\}^{1-\delta_i}}\\ &=\prod_{i=1}^{N}{ \left\{h \left(t_i\right)\right\}^{\delta_i} \cdot S \left(t_i\right)}\tag{10} \end{align} と表現することもできます。
式 $(10)$ に比例ハザードモデルの式を適用すると、 \begin{align} L \left(\boldsymbol{\beta}\right)=\prod_{i=1}^{N}{ \left\{h_0 \left(t_i\right) \cdot r \left(\boldsymbol{x}_\boldsymbol{i},\boldsymbol{\beta}\right)\right\}^{\delta_i} \cdot \left\{S_0 \left(t_i\right)\right\}^{r \left(\boldsymbol{x},\boldsymbol{\beta}\right)}} \end{align} 対数尤度関数は、 \begin{align} l \left(\boldsymbol{\beta}\right)&=\sum_{i=1}^{N} \left[\delta_i \left\{\log{h_0 \left(t_i\right)}+\log{r \left(\boldsymbol{x}_\boldsymbol{i},\boldsymbol{\beta}\right)}\right\}+r \left(\boldsymbol{x}_\boldsymbol{i},\boldsymbol{\beta}\right)\log{S_0 \left(t_i\right)}\right]\\ &=\sum_{i=1}^{N} \left[\delta_i \left\{\log{h_0 \left(t_i\right)}+\log{e^{\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}}}\right\}+e^{\boldsymbol{x}^\boldsymbol{T}\boldsymbol{\beta}}\log{S_0 \left(t_i\right)}\right]\\ &=\sum_{i=1}^{N} \left\{\delta_i \cdot \log{h_0 \left(t_i\right)}+\delta_i \cdot \boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}+e^{\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}} \cdot \log{S_0 \left(t_i\right)}\right\}\\ &=\sum_{i=1}^{N}{\delta_i \cdot \log{h_0 \left(t_i\right)}}+\sum_{i=1}^{N}{\delta_i \cdot \boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}}+\sum_{i=1}^{N}{e^{\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}} \cdot \log{S_0 \left(t_i\right)}}\tag{11} \end{align}
すなわち、興味のある未知のパラメータ $\boldsymbol{\beta}$、特定されていない基準ハザード関数と基準生存関数の各部分に分割されます。基準ハザード関数と基準生存関数は1対1の関係にあるため、どちらかが求まれば、もういっぽうを求めることができます。しかし、最尤法によってパラメータの推定を行うためには、式 $(11)$ を最大化する $\boldsymbol{\beta},h_0 \left(t\right),S_0 \left(t\right)$ を求める必要がありますが、結論を言えば、一般的にはそれが不可能であることが知られています$^\mathrm{(6)}$。ただ、交絡因子の調整という文脈においては、基準ハザード関数の形が分からなくても各共変量の影響度合いは把握することができるので、未知のパラメータ $\boldsymbol{\beta}$ だけでも推定することができれば、最低限の目的は果たすことができます。
部分尤度法
未知のパラメータ $\boldsymbol{\beta}$ だけを推定する方法は、部分尤度法 partial likelihood method(あるいは偏尤度) と呼ばれています。部分尤度法は、Cox(1972)$^\mathrm{(5)}$によって提案された方法です。Coxは、興味のあるパラメータだけに依存する部分尤度関数 partial likelihood function の利用を提案し、部分尤度関数から得られたパラメータ推定量が、完全な尤度にもとづく推定量と同じ分布特性をもつと考えました。すなわち、一致性や漸近正規性、漸近有効性などの最尤推定量がもっている好ましい性質をもっているはずという考えです。これは、Coxが提唱した時点では予想にすぎず、数学的に厳密な証明は与えられていませんでしたが、後に、マルチンゲールにもとづく計数過程の理論によって、この予想の正しさが証明されました$^\mathrm{(3,7)}$。
部分尤度法において、回帰係数を推定するための部分尤度は、タイデータがない($d_i=1$)との条件下において、時点 $t_i$ においてリスク集合に含まれる人を $R \left(t_i\right)$ として、 \begin{align} L_P \left(\boldsymbol{\beta}\right)=\prod_{i=1}^{N} \left\{\frac{e^{\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}}}{\sum_{j\in R \left(t_i\right)} e^{\boldsymbol{x}_\boldsymbol{j}^\boldsymbol{T}\boldsymbol{\beta}}}\right\}^{\delta_i}\tag{12} \end{align} で与えられます。 これは、打ち切り例 $\delta_i=0$ は部分尤度に寄与せず、イベントが発生した人の情報のみを用いることを意味しています。打ち切り例を取り除き、全部で $M$ 個のイベントが発生した場合、 \begin{align} L_P \left(\boldsymbol{\beta}\right)=\prod_{i=1}^{M}\frac{e^{\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}}}{\sum_{j\in R \left(t_i\right)} e^{\boldsymbol{x}_\boldsymbol{j}^\boldsymbol{T}\boldsymbol{\beta}}}\tag{13} \end{align} 対数部分尤度関数は \begin{align} l_P \left(\boldsymbol{\beta}\right)=\sum_{i=1}^{M} \left\{\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}-\log{ \left(\sum_{j\in R \left(t_i\right)} e^{\boldsymbol{x}_\boldsymbol{j}^\boldsymbol{T}\boldsymbol{\beta}}\right)}\right\}\tag{14} \end{align} となります。 ここから式 $(14)$ を $\beta_i$ で偏微分してスコア関数を求め、ニュートン・ラフソン法などの反復計算によって、最尤推定量を求めます。このように、比例ハザードモデルでは、共変量の影響についてはパラメトリックな推定を行いますが、ベースライン・ハザードの部分については、特定のパラメータに依存しないかたちのままにしておく(完全なパラメトリックモデルではない)という意味で、セミパラメトリック回帰モデル semi-parametric regression model と呼ばれることもあります。
回帰係数の信頼区間と検定
こうした部分尤度法にもとづいて推定された推定量は、先述の通り、他の最尤推定量と同様、漸近正規性や漸近有効性などの性質があるため、それらの性質を利用した信頼区間の算出や検定を行うことができます。
まず、信頼区間については、漸近的に \begin{gather} {\hat{\beta}}_i \sim \mathrm{N} \left[\beta_i,V \left({\hat{\beta}}_i\right)\right] \end{gather} となるため、 $100 \left(1-\alpha\right)\%$ 信頼区間は、 \begin{gather} 100 \left(1-\alpha\right)\%\ \mathrm{C.I.}: \left[{\hat{\beta}}_i\pm Z_{0.5\alpha} \cdot \mathrm{S.E.} \left({\hat{\beta}}_i\right)\right] \end{gather} で与えられます。
回帰係数の検定については、部分尤度比検定、ワルド検定、スコア検定などの方法がありますが、ワルド検定では、
\begin{gather}
Z=\frac{{\hat{\beta}}_i}{\mathrm{S.E.} \left({\hat{\beta}}_i\right)} \sim \mathrm{N} \left(0,1\right)\\
\Leftrightarrow\chi^2=\frac{{\hat{\beta}}_i^2}{V \left({\hat{\beta}}_i\right)} \sim \chi^2 \left(1\right)
\end{gather}
を利用し、
帰無仮説:共変量 $X_i$ はハザードに影響を与えない
対立仮説:共変量 $X_i$ はハザードに影響を与える(両側検定)
\begin{gather}
H_0:\beta_i=0 \quad H_1:\beta_i \neq 0
\end{gather}
の検定を行います。
部分尤度法の例
では、部分尤度の計算方法の例$^\mathrm{(8)}$を見ていきたいと思います。比例ハザードモデルにおいて、共変量 $\boldsymbol{x}$ を含む項 $r \left(\boldsymbol{x},\boldsymbol{\beta}\right)$ を表現の節約のため $\boldsymbol{\Phi} \left(\boldsymbol{x}\right)$ で表します。以下のようにイベントが発生したとします。
|
時点 $t_j$ |
個体番号 $i$ |
イベント発生 $\delta_i$ |
|---|---|---|
| $t_1$ | $3$ | $1$ |
| $t_2$ | $4$ | $1$ |
| $t_3$ | $1$ | $1$ |
| $t_4$ | $2$ | $1$ |
この例では3→4→1→2 の順で個体にイベントが発生しています。このようなイベントのパターンが得られる確率を考えてみる。$t_1$ の時点で個体3にイベントが起きているわけですが、この事象の起きる確率を、次のように時点に関する情報と個体に関する情報に分けて考えます。
{時点 $t_1$ で個体3にイベントが起きる確率}={時点 $t_1$ でイベントが1件起きる確率}×{時点 $t_1$ でイベントが1件起きたという条件の下で、それが個体3である確率}
時点 $t_1$ でイベントが1件起きる確率を求めるためには、生存時間分布に関して明示的なモデルを立てなければ記述できませんが、個体1、2、3、4のどれかにイベントが起きたという条件付きでそれが個体3であるという確率の方は、個体 $i$ のハザード関数を $h_i$、$\boldsymbol{\Phi} \left(\boldsymbol{x}_\boldsymbol{i}\right)$ を $\boldsymbol{\Phi}_\boldsymbol{i}$ と表記すると $h_i=h_0 \cdot \boldsymbol{\Phi}_\boldsymbol{i}$ の関係から \begin{gather} P_1=\frac{h_3}{h_1+h_2+h_3+h_4}=\frac{h_0 \cdot \boldsymbol{\Phi}_\boldsymbol{3}}{h_0 \left(\boldsymbol{\Phi}_\boldsymbol{1}+\boldsymbol{\Phi}_\boldsymbol{2}+\boldsymbol{\Phi}_\boldsymbol{3}+\boldsymbol{\Phi}_\boldsymbol{4}\right)}=\frac{\boldsymbol{\Phi}_\boldsymbol{3}}{\boldsymbol{\Phi}_\boldsymbol{1}+\boldsymbol{\Phi}_\boldsymbol{2}+\boldsymbol{\Phi}_\boldsymbol{3}+\boldsymbol{\Phi}_\boldsymbol{4}} \end{gather} となります。 時点1については、個体1~4 のいずれについてもイベントが起きる可能性があるので、分母は $h_1+h_2+h_3+h_4$ となっています。
比例ハザードモデルの下では、ハザード関数は、時間による効果を表す項 $h_0 \left(t\right)$ と共変量による効果を表す項 $\boldsymbol{\Phi} \left(\boldsymbol{x}_\boldsymbol{i}\right)$ の積となり、分子・分母に共通な $h_0 \left(t\right)$ が相殺することから、条件付き確率は共変量の関数 $\boldsymbol{\Phi}_\boldsymbol{i}$ のみで表せることになります。時点2における同様の条件付き確率については、個体3には既にイベントが起きているので、イベントが起きる可能性があるのは、個体1、2、4 のみです。したがって、条件付き確率は次のようになります。 \begin{gather} P_2=\frac{h_4}{h_1+h_2+h_4}=\frac{\boldsymbol{\Phi}_\boldsymbol{4}}{\boldsymbol{\Phi}_\boldsymbol{1}+\boldsymbol{\Phi}_\boldsymbol{2}+\boldsymbol{\Phi}_\boldsymbol{4}} \end{gather} このように確率を、時点に関する部分と、時点が与えられた下での条件付き確率に分解して、条件付き確率のみ掛け合わせると次のようになります。 \begin{align} L_P&=\frac{h_3}{h_1+h_2+h_3+h_4}\times\frac{h_4}{h_1+h_2+h_4}\times\frac{h_1}{h_1+h_2}\times\frac{h_2}{h_2}\\ &=\frac{\boldsymbol{\Phi}_\boldsymbol{3}}{\boldsymbol{\Phi}_\boldsymbol{1}+\boldsymbol{\Phi}_\boldsymbol{2}+\boldsymbol{\Phi}_\boldsymbol{3}+\boldsymbol{\Phi}_\boldsymbol{4}}\times\frac{\boldsymbol{\Phi}_\boldsymbol{4}}{\boldsymbol{\Phi}_\boldsymbol{1}+\boldsymbol{\Phi}_\boldsymbol{2}+\boldsymbol{\Phi}_\boldsymbol{4}}\times\frac{\boldsymbol{\Phi}_\boldsymbol{1}}{\boldsymbol{\Phi}_\boldsymbol{1}+\boldsymbol{\Phi}_\boldsymbol{2}}\times\frac{\boldsymbol{\Phi}_\boldsymbol{2}}{\boldsymbol{\Phi}_\boldsymbol{2}} \end{align} $L_P$ は、全体の尤度から時点に関する尤度を除いたものであり、これが部分尤度となります。部分尤度は、基準ハザード関数に依存しない共変最だけの関数です。
以下のような打ち切りがある場合は、次のようになります。打ち切りを受けた個体4 は、部分尤度の分母のみにしか寄与しません。 \begin{align} L_P&=\frac{h_3}{h_1+h_2+h_3+h_4}\times\frac{h_1}{h_1+h_2}\times\frac{h_2}{h_2}\\ &=\frac{\boldsymbol{\Phi}_\boldsymbol{3}}{\boldsymbol{\Phi}_\boldsymbol{1}+\boldsymbol{\Phi}_\boldsymbol{2}+\boldsymbol{\Phi}_\boldsymbol{3}+\boldsymbol{\Phi}_\boldsymbol{4}}\times\frac{\boldsymbol{\Phi}_\boldsymbol{1}}{\boldsymbol{\Phi}_\boldsymbol{1}+\boldsymbol{\Phi}_\boldsymbol{2}}\times\frac{\boldsymbol{\Phi}_\boldsymbol{2}}{\boldsymbol{\Phi}_\boldsymbol{2}} \end{align} カプラン・マイヤー推定量を求めるときには、どの個体にイベントが起きたかは気にせずに、その時点を越えて生き残る割合をかけていったことから、カプラン・マイヤー推定量は、イベント発生パターンのすべての情報のうち時点に関する情報のみを利用します。これに対しコックス回帰は、時点を無視して個体の情報のみを利用した回帰分析となります。
|
時点 $t_j$ |
個体番号 $i$ |
イベント発生 $\delta_i$ |
|---|---|---|
| $t_1$ | $3$ | $1$ |
| $t_2$ | $4$ | $0$ |
| $t_3$ | $1$ | $1$ |
| $t_4$ | $2$ | $1$ |
比例ハザード性の検証方法
比例ハザード性は、コックス比例ハザードモデルの大前提であり、この仮定が成り立っていないと、モデルの妥当性が損なわれてしまいます。誤った判断をしないためには、得られたデータにもとづいて、比例ハザード性を個々の共変量ごとにその都度検証する必要があります。
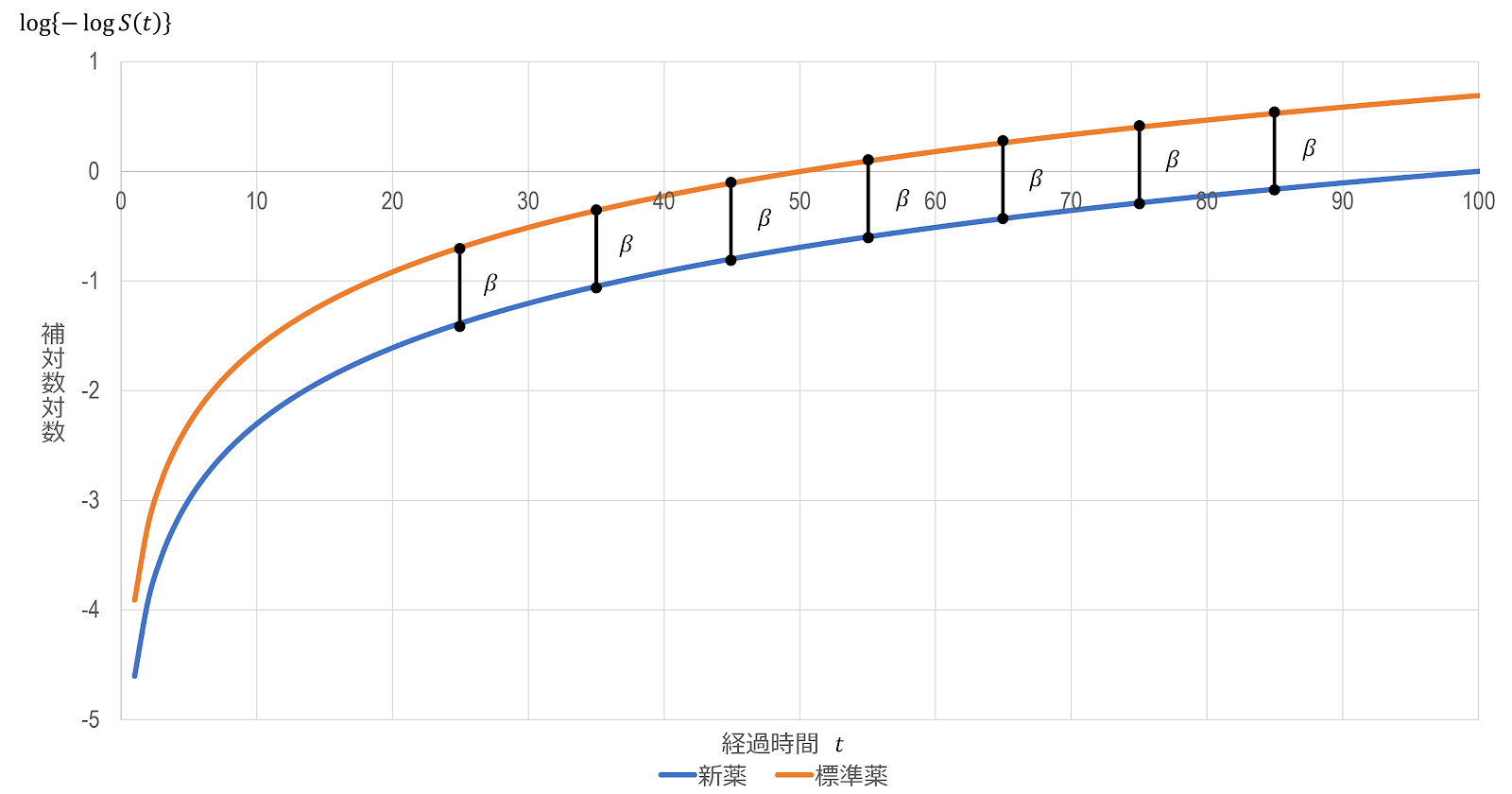
これには、(1)カプラン・マイヤープロットの形状から判断する(交叉していたり、群間差が異常に広がったりしていたら比例ハザード性は疑わしい)、(2)カプラン・マイヤープロットから得られるMST比とハザード比が逆比例かを確認する(指数分布に近い場合、MST比とハザード比が逆比例していなければ比例ハザード性は疑わしい)、(3)補対数対数プロット log-log plots を利用して判断する、(4)時間 $t$ と共変量 $X_i$ との交互作用の検定を行う、(5)Schoenfeld residualst などに基づく特別の検定で確認するなどの方法があります。ここでは、代表的な方法である(3)補対数対数プロットによる方法を紹介します。
補対数対数プロットによるグラフ表現
補対数対数プロットでは、生存関数と累積ハザード関数の関係を使用します。式 $(4),(5)$ の関係式より、 \begin{align} H \left(t\middle|\boldsymbol{x}\right)=H_0 \left(t\right) \cdot e^{\boldsymbol{x}^\boldsymbol{T}\boldsymbol{\beta}} \end{align} \begin{align} S \left(t\middle|\boldsymbol{x}\right)&=\exp \left\{-H \left(t\middle|\boldsymbol{x}\right)\right\}\\ &=\exp \left\{-H_0 \left(t\right) \cdot e x p \left(\boldsymbol{x}^\boldsymbol{T}\boldsymbol{\beta}\right)\right\} \end{align} したがって、 \begin{gather} \log{S \left(t\middle|\boldsymbol{x}\right)}=-H_0 \left(t\right) \cdot \exp \left(\boldsymbol{x}^\boldsymbol{T}\boldsymbol{\beta}\right)\\ -\log{S \left(t\middle|\boldsymbol{x}\right)}=H_0 \left(t\right) \cdot \exp \left(\boldsymbol{x}^\boldsymbol{T}\boldsymbol{\beta}\right)\\ \log{ \left\{-\log{S \left(t\middle|\boldsymbol{x}\right)}\right\}}=\log{H_0 \left(t\right)}+\boldsymbol{x}^\boldsymbol{T}\boldsymbol{\beta} \end{gather}
簡単のため、共変量が1つの場合を考えます。例えば、薬物投与群を $x=1$、対照群を $x=0$ とすると、比例ハザード性が成り立っていれば、2群の間で $\log{ \left\{-\log{S \left(t\middle| x\right)}\right\}}$ と経過時間($\log{t}$ あるいは $t$)のプロットは平行になり、縦軸方向の距離は、2値変数 $x$ に対するコックス回帰の係数 $\beta$(層間の相対ハザードの対数)になります。
このことを利用し、グラフから補対数対数曲線が平行かどうかを判断します。
参考文献
- 大橋 靖雄, 浜田 知久馬 著. 生存時間解析:SASによる生物統計. 東京大学出版会, 1995, p.105-114
- 前谷 俊三 著. 臨床生存分析:生存データと予後因子の解析. 南江堂, 1996, p.141-150
- ダグラス・アルトマン 著, 木船 義久, 佐久間 昭 訳. 医学研究における実用統計学. サイエンティスト社, 1999, p.312-316
- デーヴィッド・マシューズ, ヴァーノン・フェアウェル 著, 宮原 英夫, 折笠 秀樹 監訳, 小田 英世, 手良向 聡, 森田 智視 訳. 実践医学統計学. 朝倉書店, 2005, p.137-148
- 中村 剛 著. Cox比例ハザードモデル. 朝倉書店, 2001, p.33-44
- デビッド・ホスマー, スタンリー・レメショウ, スーザン・メイ 著, 五所 正彦 監訳. 生存時間解析入門. 東京大学出版会, 2014, p.71-90
- ジョン・ラチン 著, 宮岡 悦良 監訳, 遠藤 輝, 黒沢 健, 下川 朝有, 寒水 孝司 訳. 医薬データのための統計解析. 共立出版, 2020, p.490-494
- 赤澤 宏平. 生存時間データの解析. 医療情報学. 2001, 20(6), p.451-461, doi: 10.14948/jami.20.451
- 小柳 貴裕. 統計学 整形外科医が知っておきたい: (12)比例ハザード モデル:比例という名のハードル. 臨床整形外科. 2004, 39(10), p.1326-1332.
- Bradburn, M.J., Clark, T.G., Love, S.B. et al.. Survival analysis part II: multivariate data analysis-an introduction to concepts and methods. Br J Cancer. 2003, 89(3), p.431-436, doi: 10.1038/sj.bjc.6601119
- George, B., Seals, S. & Aban, I.. Survival analysis and regression models. J Nucl Cardiol. 2014, 21(4), p.686-694, doi: 10.1007/s12350-014-9908-2
- 藤田 烈. 疫学・統計解析シリーズ:生存時間解析結果を読み解くための基礎知識. 日本環境感染学会誌. 2014, 29(5), p.313-323, doi: 10.4058/jsei.29.313
引用文献
- Kleinbaum, D.G. & Klein, M.. Survival Analysis: A Self-Learning Text. Third Edition, Springer, 2011, 715p.
- デービット・コレット 著, 宮岡 悦良 監訳. 医薬統計のための生存時間データ解析. 共立出版, 2013, 422p.
- Andersen, P.K., Borgan, Ørnulf, Gill, R.D. et al.. Statistical Models Based on Counting Processes. Springer Verlag, 1993, 784p.
- Wei, L.J.. The accelerated failure time model: A useful alternative to the cox regression model in survival analysis. Statistics in Medicine. 1992, 11(14-15), p.1871-1879, doi: 10.1002/sim.4780111409
- Cox, D.R.. Regression Models and Life-Tables. Journal of the Royal Statistical Society. Series B (Methodological). 1972, 34(2), p.187-220, doi: 10.1007/978-1-4612-4380-9_37
- Kalbfleisch, J.D. & Prentice, R.L.. The Statistical Analysis of Failure Time Data. 2nd Edition, John Wiley & Sons, Inc., 2002, 462p.
- Fleming, T.R. & Harrington, D.P.. Counting Processes and Survival Analysis. Wiley & Sons, Inc., 2005, 454p.
- 大橋 靖雄, 浜田 知久馬 著. 生存時間解析:SASによる生物統計. 東京大学出版会, 1995, p.112-113



0 件のコメント:
コメントを投稿