医学・疫学研究では、イベント発生の有無ではなく、イベント発生までの時間が主たる関心となることがあり、そのような目的のために用いられる解析手法は生存時間分析と呼ばれています。本稿では、生存時間分析の基本である、観察の打ち切り、生存関数、ハザード関数、累積ハザード関数などについて解説しています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
生存時間分析とは?
生きとし生けるすべてのものは、「死」という運命から逃れることはできません。場末のしがない労働者であっても、世界最高の権力者であってもそれは変わらぬ定めです。「死」が避けがたい運命であるならば、甘んじてそれを受け入れ、次善の策として、人々は「どれくらい良く、そして長く生きられるか」を問題とします。
医学・疫学研究を実施する側にとっても、「死亡」は主要なアウトカムのうちのひとつであり、特に、がんなどの慢性疾患では主要なエンドポイントとして採用されることが少なくありません。そこでは、「イベントが発生するか否か」ではなく、「どれくらい長い間、イベントが発生しないか」が問題となり、「従来の治療法に比べて新しい治療法はどれくらい生き長らえさせることができるか?」といったことが検証されます。このように、関心のあるイベントが発生するまでの時間 time−to−event を主要な検証課題とする研究分野は生存時間分析 survival analysis, life time data analysis と呼ばれています。
「生存」時間の意味
生存時間分析は、もともと医学・疫学研究のために開発され、その名が示す通り、人の「生死」を主要なエンドポイントとしていました。しかし現在では、物理、工学、経済学、社会学、心理学などさまざまな分野でも応用されており、生存時間 survival time, failure time の概念もそれに合わせて、ある起点から特定のイベントが起こるまでの時間という広い意味に拡張されています。
臨床医学の分野では、例えば抗がん剤の臨床試験において、試験治療を開始してから「死亡」するまでの時間はもちろんのこと、がんが「再発」するまでの時間(無再発生存期間 relapse-free survival)、「増悪するか死亡するか」までの時間(無増悪生存期間 progression-free survival)などが関心のあるエンドポイントとなり得ます。
感染制御の分野では、入院患者が薬剤耐性菌を保菌するまでの期間(無感染期間)や感染症を発症するまでの期間、人工呼吸器や中心ラインなどの医療器具の使用開始から関連する感染症を発症するまでの期間、あるいは、特定の感染症を発症してから死亡あるいは重症化するまでの期間などを挙げることができます。
信頼性工学の分野では、システムの故障を反応とみなすことがあり、工業製品の寿命に関心がある場合があります。この意味では故障または破綻 failure time という言葉が用いられます。
また、死亡などの悪いイベントだけでなく、「仕事の再開」、「退院」、骨髄移植における「生着」など、対象者にとって良いイベントが起こるまでの時間も生存時間として扱うことができます。この場合、生存時間は短いほうが好ましく、悪いイベントである場合は生存時間が長いほうが好ましいことになります。
本稿では特に断らない場合、生存時間分析の対象を医薬・疫学の分野に限定し、悪いイベントを関心のあるイベントとし、一般的なイベントという意味で「死亡」を、イベント発現までの時間という意味で「生存時間」という用語を用います。
生存関数と累積発生率
生存時間データは、観察を始めてからイベントが発生するまでの時間として与えられます。例えば、人の寿命について考えてみましょう。この場合、観察の開始はその人の生誕、イベントの発生は死亡の瞬間ということになります。生存時間分析では、最も基本的な指標として、生存関数というものを考えます。今から、この生存関数について説明したいのですが、話の本質をつかみやすくするために、すべての人間の生涯を見通せる神様の立場になって考えてみたいと思います。
記号の定義
神様になったあなたは、超越的な力によってすべての人の全生涯を観察することができます。今、関心があるのは、人々の生存時間ということになりますが、Aさんは84年、Bさんは70年、Cさんは29年のように、ひとりひとり生存時間は異なります。「生物学的な限界が高々120歳くらいとされていて、衛生や栄養の状況が日々改善されているので、何もなければだいたい70年くらいは生きられて、…」というようなことは分かりますが、細かい点については絶対的な法則があるわけでもないので、ひとりひとりの生存時間 $T \left( \gt 0\right)$ は非負の値を取る確率変数であると考えられます。
ここで、ある日(例えば今日)に生まれた人の集団の寿命について考えてみましょう。今日、世界中で $N$ 人が生まれ、生涯をスタートします。ある人は、衛星状況の悪い地域で生まれたため、0歳児の時点で感染症で亡くなってしまい、別の人は、波乱万丈な生涯を過ごし、ギネスの長寿記録を狙えるような期間を生き抜きました。
仮に個々人に通し番号をつけるとすると、番号 $i \left(=1,2, \cdots ,N\right)$ ひとりひとりについて、それぞれの生存時間 $t_i$ が観察され、それぞれの生存時間に対し、1件の死亡が観測されます。全体で見ると、1日のうちに複数の死亡が観測されると思われるので、一般的に、ある時点 $t_i$ における死亡者数を $d_i$ と表記します。また、後々必要となるため、$t_i$ を小さい順に並べ替えたものを $t_{ \left(i\right)}$ としておきます。すなわち、 \begin{gather} t_{ \left(1\right)} \lt t_{ \left(2\right)} \lt \cdots \lt t_{ \left(N\right)} \end{gather}
では、例えば、運命に恵まれなかった $N=10$ 人について考えてみます。この10人は、生存時間が以下のようにそれぞれ1~10日という短い生涯を閉じることになりました。生存時間は、本質的には、「1日と何時間何分何秒」という連続型変数ですが、ここではまず、1日を観測単位とする離散型変数として考えます。この例の場合は、2人が亡くなった日はなく、10人が1日おきに亡くなっているので、$d_i=1$ となります。また、死亡日を並べ替えたものについては、2番の人の生存時間が1日と1番短く、9番の人が最長なので、 \begin{gather} t_2\rightarrow t_{ \left(1\right)}=1, \cdots ,t_9\rightarrow t_{ \left(10\right)}=10 \end{gather} という要領で並べ替えられます。
| 番号 $i$ | 日数 $t$ |
|---|---|
| $2$ | $1$ |
| $8$ | $2$ |
| $7$ | $3$ |
| $4$ | $4$ |
| $1$ | $5$ |
| $3$ | $6$ |
| $6$ | $7$ |
| $5$ | $8$ |
| $10$ | $9$ |
| $9$ | $10$ |
死亡密度関数
このとき、全体のうち、ある時点 $t$ でイベントを発生する個体の割合、あるいは個人に着目すれば、その人がある時点 $t$ でイベントを発生する確率を死亡密度関数 death density function、あるいは狭義の死亡率と呼び、 \begin{gather} f \left(t\right)=P \left(T=t\right) \end{gather} と定義します。 具体的には、ある時点 $t_i$ に対して、 \begin{gather} f \left(t_i\right)=\frac{d_i}{N} \end{gather} この例の場合は、 \begin{gather} f \left(1\right)=f \left(2\right)= \cdots =f \left(10\right)=\frac{1}{10}=0.1 \end{gather} となります。
死亡密度関数は、一般的な確率変数における確率関数・確率密度関数の生存時間分析における呼び方であり、 \begin{gather} f \left(t\right)\in \left[0,1\right] \end{gather} などの性質が成り立ちます。
累積発生率
また、全体のうち、ある時点 $t$ までにイベントを発生している個体の割合、その人がある時点 $t$ までにイベントを発生している確率を累積発生率 cumulative incidence rate と呼び、 \begin{gather} F \left(t\right)=P \left(T \le t\right) \end{gather} と定義します。 具体的には、ある時点 $t_i$ に対して、 \begin{gather} F \left(t_i\right)=\sum_{j=1}^{i}\frac{d_j}{N} \end{gather} この例の場合、例えば、 \begin{gather} f \left(5\right)=\frac{1+1+1+1+1}{10}=\frac{5}{10}=0.5 \end{gather} となります。
累積発生率は、一般的な確率変数における分布関数と同様、 \begin{gather} F \left(t\right)\in \left[0,1\right]\\ F \left(0\right)=0 \quad \lim_{t\rightarrow\infty}{F \left(t\right)}=1 \end{gather} などの性質が成り立ちます。
生存関数
これら2つの指標は、「イベントが発生すること」に着目した指標ですが、生存時間分析では、「イベントが発生しない時間」が主たる関心事です。これを表すのが生存関数という指標です。
生存関数 survival function とは、全体のうち、ある時点 $t$ までにイベントが発生していない個体の割合、その人がある時点 $t$ までにイベントが発生していない確率を表し、”survival” の頭文字をとって、よく、 \begin{gather} S \left(t\right)=P \left(t \le T\right)=1-F \left(t\right) \end{gather} と定義されます。 具体的には、ある時点 $t_i$ に対して、 \begin{gather} S \left(t_i\right)=1-\sum_{j=1}^{i}\frac{d_j}{N} \end{gather} この例の場合、例えば、 \begin{gather} f \left(7\right)=1-\frac{7}{10}=0.3 \end{gather} となります。
生存関数は、生存確率関数 survival probability function、累積生存率 cumulative survival rate などとも呼ばれます。疫学の有病率と同様、本質的には、「割合」に対応する量です。
生存関数は累積発生率と同様、 \begin{gather} S \left(t\right)\in \left[0,1\right]\\ S \left(0\right)=1 \quad \lim_{t\rightarrow\infty}{S \left(t\right)}=0 \end{gather} などの性質が成り立ちます。 すなわち、経過時間 $t$ に対する単調非増加関数であり、観測開始時点では1、観測から時間が経つにつれて、0に漸近していきます。
今回の例の場合、死亡密度、累積死亡率、生存関数をまとめると、以下の表のようになります。
| 番号 $i$ | 日数 $t$ | 死亡密度 $f \left(t\right)$ | 累積死亡率 $F \left(t\right)$ | 生存関数 $S \left(t\right)$ |
|---|---|---|---|---|
| $2$ | $1$ | $\frac{1}{10}$ | $\frac{1}{10}$ | $\frac{9}{10}$ |
| $8$ | $2$ | $\frac{1}{10}$ | $\frac{2}{10}$ | $\frac{8}{10}$ |
| $7$ | $3$ | $\frac{1}{10}$ | $\frac{3}{10}$ | $\frac{7}{10}$ |
| $4$ | $4$ | $\frac{1}{10}$ | $\frac{4}{10}$ | $\frac{6}{10}$ |
| $1$ | $5$ | $\frac{1}{10}$ | $\frac{5}{10}$ | $\frac{5}{10}$ |
| $3$ | $6$ | $\frac{1}{10}$ | $\frac{6}{10}$ | $\frac{4}{10}$ |
| $6$ | $7$ | $\frac{1}{10}$ | $\frac{7}{10}$ | $\frac{3}{10}$ |
| $5$ | $8$ | $\frac{1}{10}$ | $\frac{8}{10}$ | $\frac{2}{10}$ |
| $10$ | $9$ | $\frac{1}{10}$ | $\frac{9}{10}$ | $\frac{1}{10}$ |
| $9$ | $10$ | $\frac{1}{10}$ | $\frac{10}{10}$ | $\frac{0}{10}$ |
死亡密度関数と累積発生率の関係
生存時間分析における「死亡密度関数」と「累積発生率」との関係は、一般的な確率論における「確率密度関数」と「累積分布関数」の関係と同じです。したがって、 \begin{gather} F \left(t\right)= \left\{\begin{matrix}\sum_{x=0}^{t}f \left(x\right)&\mathrm{Discrete}\\\int_{x=0}^{t}f \left(x\right)dx&\mathrm{Continuous}\\\end{matrix}\right.\\ f \left(t\right)=\frac{d}{dx}F \left(t\right)=\lim_{\Delta t\rightarrow0}{\frac{F \left(t+\Delta t\right)-F \left(t\right)}{\Delta t}} \end{gather} の関係が成り立ちます。
生存曲線
生存関数が登場する身近な例に、毎年厚生労働省が発表している「簡易生命表」があります。簡易生命表の意味や作成の目的は、以下のように説明されています。
生命表は、ある期間における死亡状況(年齢別死亡率)が今後変化しないと仮定したときに、各年齢の者が1年以内に死亡する確率や平均してあと何年生きられるかという期待値などを死亡率や平均余命などの指標(生命関数)によって表したものである。特に、0歳の平均余命である「平均寿命」は、死亡状況を集約したものとなっており、保健福祉水準を総合的に示す指標として広く活用されている。
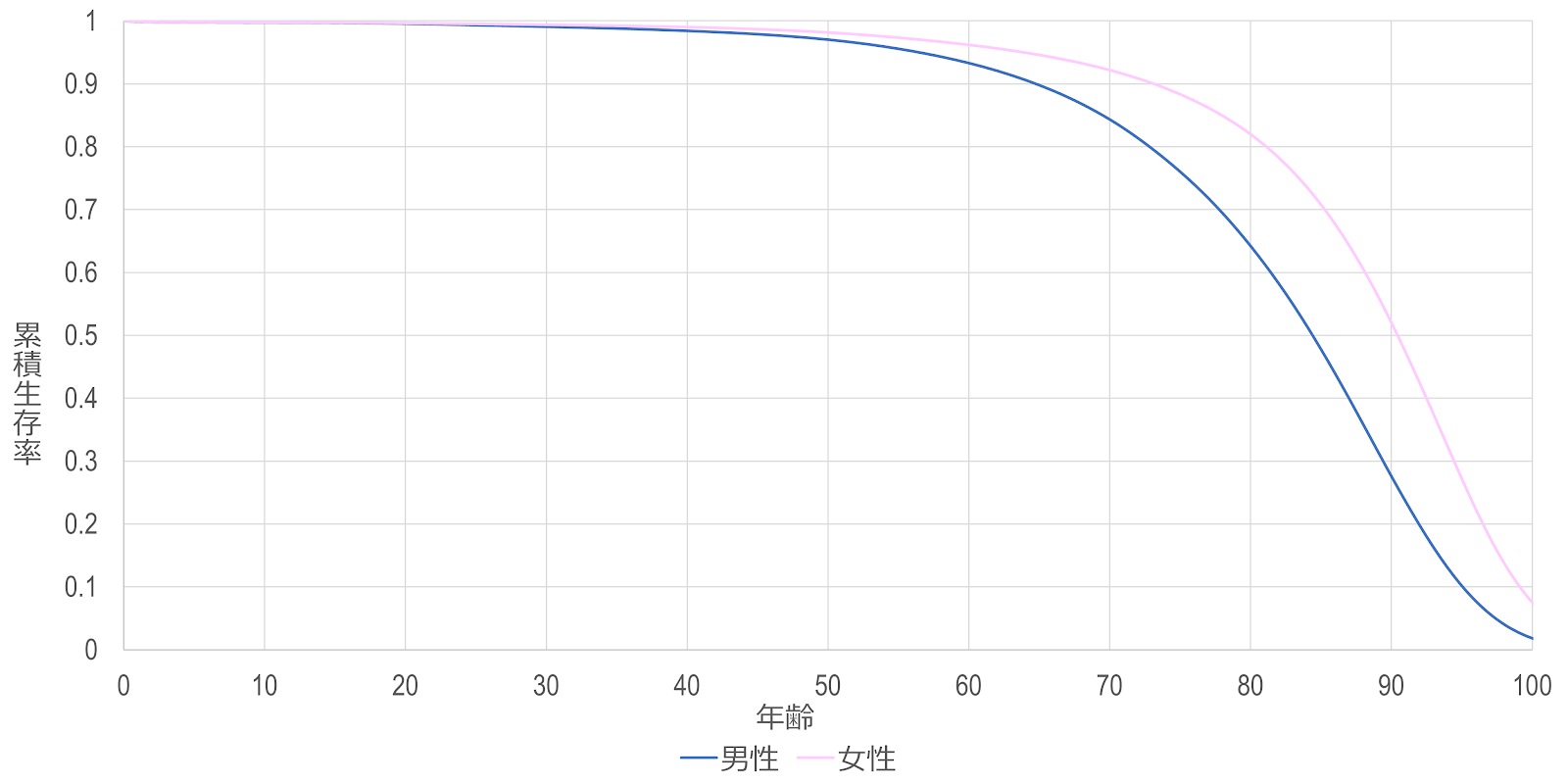
このような生命表を用いると、生存曲線を描くことができます。生存曲線 survival curve、あるいは累積生存率曲線 cumulative survival rate curve とは、縦軸に生存割合、横軸に経過時間をとったグラフのことを指します。例えば、2021年の日本人の生存曲線は以下のようになります。
| 年齢 | 男性 | 女性 |
|---|---|---|
| $0$ | $1.000$ | $1.000$ |
| $10$ | $0.997$ | $0.998$ |
| $20$ | $0.995$ | $0.996$ |
| $30$ | $0.991$ | $0.994$ |
| $40$ | $0.984$ | $0.990$ |
| $50$ | $0.970$ | $0.981$ |
| $60$ | $0.933$ | $0.962$ |
| $70$ | $0.843$ | $0.922$ |
| $80$ | $0.642$ | $0.819$ |
| $90$ | $0.275$ | $0.520$ |
| $100$ | $0.018$ | $0.075$ |
生存曲線の特徴を表わす数的指標
生存曲線を見れば、ある集団(群)の生存時間の分布が視覚的に分かりますが、図の代わりに生存曲線の特徴を数値で要約する指標もあります。
医学的によく使われているものには、特定の時点における生存率や生存時間中央値、平均生存時間(厳密には算術平均値)などがあります。また、生存期間の標準偏差や最大値・最小値も生存時間の分布の特徴の一端を表わしています。
この中で標準偏差に比べて最大値は群の例数が増えるほど大きくなり、最小値は小さくなる傾向があます。また、標本間のばらつきも大きく、別稿で見るような生存曲線の比較をする場合、妥当性が問題となります。
中央値と比べると平均値にも多少この傾向があり、極端な値に影響されやすい指標です。また、実際に研究をする際、この後に見るように、調査期間内に全員のイベントが観測されないと、平均値や最大値は計算できません。こうしたことから、平均値はやや使いにくい指標とされています。
ある特定の時点の生存率も臨床的にしばしば使用されます。特にがん診療においては、5年生存率 five-year survival rate は全治率に近い指標として多用されています。ただ経過の長いがんでは5年以後の再発は決して稀ではありません。5年生存率が0の生存率曲線の中には5年目に始めて0になる場合もあれば、既に1年目で0になる場合もあり、両者には生存時間で大きい違いがあります。
この違いを示すためには短期生存群では、生存時間中央値を用いることができます。生存時間中央値 median survival time: MST とは、累積生存率がちょうど50%になる時点を指します。しかし、逆に予後の非常によい集団では、調査期間中に累積生存率が0.5以下に低下せず生存時間中央値が求められない場合もあります。
観察の打ち切り
前節では、超越的な存在となって、観察対象としたい人々を観測することができました。しかし、実際には、すべての人のイベント発生を観測できるとは限りません。
コホート研究や介入研究など追跡型の研究では対象者をベースライン・データとともに登録し、追跡していきます。しかし、研究開始とともに全症例が登録され、研究終了までその全員が追跡できるわけではありません。臨床研究では受診時に登録することが多いので登録時点が人によって異なり、いつの間にか病院に来なくなることもあって、観察期間はバラバラになりがちです。
くわえて、臨床試験では、登録されたすべての症例がイベント発現するまで追跡することも可能ですが、それでは試験完遂まであまりにも長い時間を要してしまいます。そのため通常は、あらかじめ最大追跡期間を設定しその最終時点で観察を終了します。また、症例によっては転院や転居、他の要因での死亡、研究参加の取り下げなどによって追跡不能になってしまうこともあります。
このように関心のあるイベントが発生する前に観察を終了してしまうことを打ち切り censoring と呼びます。打ち切り例 censored case においては、関心のあるイベントがいつ発生したかは不明で、正確な生存時間は分からないという点が特徴です。
打ち切りには、以下のようなパターンがあります。
追跡不能・脱落
追跡不能 lost to follow up・脱落 drop out とは、(主に)被験者の状態や事情、都合などにより、追跡ができなくなったり、研究への参加を取りやめたりすることです。例えば、「研究期間の途中で転院し、その後の足取りが追えなくなる」、「状態が良くなったため研究から離脱し、通常の生活に戻る」、「状態が悪化したため、介入処理と観察を中止し、新たな治療に移る」、「心境の変化により、臨床試験への協力を取りやめる」などのパターンがあります。
競合リスクによる死亡
競合リスク competitive risk とは、関心のあるイベントの観察を困難にする要因のことを指します。例えば、「肺がんによる死亡」をエンドポイントとしている場合に、「心筋梗塞によって、被験者が死亡してしまった」という場合、「心筋梗塞」が競合リスクに該当します。患者が「心筋梗塞」によって死亡してしまった場合、「肺がんによる死亡」は観察できなくなり、その時点で観察を打ち切らざるを得なくなります。
研究期間の満了
先に述べたように、臨床研究では実務上、研究期間があらかじめ設定されており、全被験者が一斉に観察を開始するわけでもありません。例えば、5年の研究期間において、Aさんは研究開始時点から観察を開始し、Bさんは、4年目の終わりに研究に登録されたとします。このとき、幸いなことにAさんは研究終了時点でも健在でした。また、Bさんは1年間しか観察していませんが、予定していた研究期間を迎えました。このとき、2人の観察は、それぞれ5年、1年で打ち切られるということになります。
データの形式
実際の生存時間分析を行う際には、このような打ち切りが存在します。後述するように、打ち切りデータを無視してデータの解析を行ってしまうと、結果の妥当性が損なわれてしまうおそれがあるため、そのデータは「イベントが観測されたデータ」なのか「観察が打ち切られたデータ」なのかを区別する必要があります。そのため、実際にデータを取る際には、観測できた生存時間 $t_i$ とイベント発生の有無を示す指示関数 $\delta_i$ を1組としてデータ $ \left(t_i,\delta_i\right)$ を形成します。
ただし、
\begin{gather}
\delta_i= \left\{\begin{matrix}1&\mathrm{Event\ Observed}\\0&\mathrm{Censored}\\\end{matrix}\right.
\end{gather}
また、打ち切りには先に挙げた3つのパターンがありますが、通常、解析の際にこれらを区別することはありません。解析の際には、こうした原因よりも、後述するような性質にもとづいて、打ち切りデータの取り扱いを判断します。
打ち切りの種類
打ち切りには、その特徴や性質に応じて、いくつかの種類があります。打ち切りの分類方法として、打ち切りが発生する時期による分類と、イベント発生に対する情報の有無による分類があります。
発生時期による分類
右側打ち切り
右側打ち切り right-censoring とは、イペントの発生が打ち切り時点以降(右側)であり、真の生存時間が打ち切りまでの時間より長い打ち切りのことを指します。右側打ち切りには、①時間打ち切りと②個数打ち切り、③無作為打ち切りがあります。
①時間打ち切りとは、例えば、「手術後30日間観察を行う」、あるいは「研究期間は、20XX年03月31日までとする」などあらかじめ実験の終了時点を設定する場合に起こる打ち切りを指し、信頼性工学の用語では、タイプ1打ち切り type I censoring と呼びます。
②個数打ち切りとは、「感染者が10 名確認された時点で観察を完了する」、「7 個中4 個の製品が故障したら実験を打ち切って解析を始める」というように、イベントの発生が一定数に達した時点で観察を打ち切ることを指します。信頼性工学の用語では、タイプ2打ち切り type Il censoring とも呼ばれます。このような研究デザインは試験期間を短縮したりコストを節約したりするために動物実験や工業製品の寿命試験ではよく用いられます。また、近年では、動物愛護の精神から、死にかかった動物に実験を継続して死を待つより(死にかかった動物の苦痛を大きくしたり、苦痛を継続したりするだけより)、動物の苦痛状態の許容限界基準を設けて、原則的に、動物をできる限り苦痛を与えない方法で安楽死させることが研究計画の中で決められています。
③無作為打ち切り random censoring とは、転院による追跡不能、副作用による同意撤回、追跡中の死亡(他病死)など、研究者が管理できず、かつ観測される生存時間とは全く関係ない原因によって発生する打ち切りを指します。
左側打ち切り
左側打ち切り left-censoring とは、観察開始時点で、既にイベントを発生していた場合のことを指します。
左側打ち切りデータは、自覚症状が強くなく、病院などで精密な検査をしない限り発症が確認できないような事象が起きるまでの時間をエンドポイントとした場合に生じます。例えば、糖尿病の合併症である網膜症は、精密な検査を病院で行わないかぎり診断できず、検査した時点で網膜症が発症していることが分かった患者については、その時点以前に網膜症が発症したという左側打ち切りデータが得られることになります。
また、げっ歯類を用いた癌原性試験では、非致死性の腫瘍については、他の原因で動物が死亡して解剖してみない限り腫瘍の有無が確認できません。腫瘍の発生をイベントとすると、腫瘍が発生するまでの時間は左側打ち切りを受けていることになります。
区間打ち切り
区間打ち切り interval-censoring とは、イベントの発生時点が正確には分からず、ある期間の間であることのみが分かっている場合のことを指します。
例えば、がんの再発までの時間を3ヶ月ごとの定期検診で調べる場合が挙げられます。このとき、3月の検診では再発が確認できなかったが、6月の検診では再発が確認されたという場合、正確に何月何日にがんが再発したかは正確には分からず、4月~6月の間ということのみが分かることになります。
このように、発生時期による分類には3種類がありますが、これらのうち、右側打ち切りが最も一般的であるため、本稿では、単に「打ち切り」という場合、右側打ち切りのことを指すこととします。
予後に関する情報の有無による分類
情報のない打ち切り
情報のない打ち切り non-infomative censoring とは、打ち切りの有無によって、その後のイベントの起こりやすさが変わらないタイプの打ち切りを指します。右側打ち切りの中で説明した、時間打ち切り、個数打ち切り、無作為打ち切りが、無情報な打ち切りの典型例とされています。
例えば、以前ある病院の禁煙プログラムに参加し、定期健診のついでに禁煙状況の経過観察を行っていた人が、他の支店で急遽欠員が出たことによって転勤することになったとします。この場合、観察が打ち切られる理由(転勤)は、本人の禁煙に対する意思とは、基本的には無関係であり、他の支店で欠員が出なければ観察を継続できていた可能性があります。このとき、既に禁煙プログラムの受講は終わっているため、観察を続けていた場合でも、その後禁煙を続けられるかは、基本的には変わらないと推測できます。
このように、数学的には観測された生存時間 $t_i$ と打ち切りの指示関数 $\delta_i$ が互いに独立であるとき、具体的には、観察打ち切りになった個体におけるそれ以降の将来のイベントの発現可能性は、そこで観察打ち切りにならずに観察を継続している個体の将来のイベントの発現可能性と同じであることが仮定できる場合、情報のない打ち切りとみなすことができます。
情報のある打ち切り
情報のある打ち切り infomative censoring とは、打ち切りの有無によって、その後のイベントの起こりやすさに違いがあると予想されるタイプの打ち切りを指します。
例えば、がんの術後補助療法の臨床試験で、患者の状態が悪化したため行った投薬中止を打ち切りにするのがこの例にあたります。この場合、打ち切り後にイベントが発生する可能性は高いと予想されます。
打ち切り例に対する仮定
打ち切りが「情報のある打ち切り」か「情報のない打ち切り」かは、後に見るような生存関数の推定を行ううえでとても重要となります。再び、超越的な存在になり、人々の生涯を観察しているとします。現在、ある1000人を観察していて4年が経過したところで、それまでに800人の死亡が確認されました。このとき、悪魔の妨害によって、残りの200人のうち、100人の観測ができなくなってしまいました。仕方なくあなたは、残りの100人の観測を続け、5年が経過するまでに100人中10人の死亡が確認されました。
このとき、「情報のない打ち切り」は、「200人が同じ日に死亡する人のペアになっていて、そのうち片方だけが隠された場合」に相当します。そうであれば、200人中20人にイベントが発生しているわけなので、5年生存率は、 \begin{align} S \left(5\right)=\frac{180}{1000}=0.18 \end{align} と偏りなく求めることができます。
いっぽう、「情報のある打ち切り」は、例えば、「観測できなくなった直後に死亡する人だけが見えなくなった(100人は全員死亡)」という場合にあたります。このとき、真の5年生存率は、 \begin{align} S \left(5\right)=\frac{90}{1000}=0.09 \end{align} ですが、 その事情を知らずに「情報のない打ち切り」として推定すると、真の生存率よりも高い値として認識してしまいます。
こうしたことから、情報の有無はとても大切な要素となりますが、実際には得られたデータのみから、その打ち切りの情報の有無を確認することは困難です。そのため、可能な限り打ち切りが起こらないような努力が必要とされています。
本稿では話を単純にするため、以降、「打ち切り」は全て「情報のない右側打ち切り」として解説を続けます。
打ち切りデータによるバイアス
このような打ち切り例を生存率の計算上、どう取り扱うかが問題となり、文字通り、解析上での厄介者となります。
例えば、過去の手術例に関する生存時間データが以下のように得られたとします。3例は5年を越えて生存、5例は5年未満で死亡が確認されました。残りの2例は生存中ですが手術後日が浅く、5年に達していない打ち切り例とします。
| 番号 $i$ | 観測時間(年)
$t_i$ | 終了状況 $\delta_i$ |
|---|---|---|
| $1$ | $5.6$ | $1$ |
| $2$ | $6.4$ | $1$ |
| $3$ | $6.3$ | $1$ |
| $4$ | $4.8$ | $1$ |
| $5$ | $3.6$ | $1$ |
| $6$ | $2.5$ | $1$ |
| $7$ | $3.5$ | $1$ |
| $8$ | $2.3$ | $1$ |
| $9$ | $1.5$ | $0$ |
| $10$ | $1.1$ | $0$ |
まず、平均生存時間を求めてみようと思います。このとき、イベントの発生が確認された8人の生存時間は問題なく計算に取り込むことができますが、打ち切られた2例については、真の生存時間が分かりません。残りの2人は、もしかしたら打ち切られた直後にイベントが発生するかもしれませんし、10年経ってもイベントが発生しないかもしれません。この2例の真の値によって、平均値が左右されてしまうので、打ち切りデータが存在する場合、単純な方法では、生存時間の平均や分散の妥当な推定値が得られないことが分かります。
では次に、医学の分野でよく用いられる5年生存率を求めたいとします。5年生存率は5年累積死亡率(死亡率と略する)から求められるので、まずこの死亡率を求めます。この死亡率を分数で表わすとすると、分子には5年未満死亡の5例が、分母にはこの5例と、5年以上生存した3例の計8例がくると思われます。では、打ち切りの2例は分子と分母のどちらに加えるべきでしょうか。
まず、この打ち切りの2例を分子と分母にそれぞれ加え、死亡率を $\frac{7}{10}$ とすると、この2例は実際に5年未満で死亡したものと同じ扱いになります。もし、打ち切りの時点で2例とも既に末期状態にあり、到底5年生きられない場合でもなければ、この計算値は妥当ではりません。これは死亡率を高く見積りすぎていて、むしろその上限を示すことになります。
逆に打ち切り例を分母だけに加え、死亡率を $\frac{5}{10}$ にすると、打ち切り例が生存例と同じ扱いになります。もし、打ち切りがともに5年直前であり、2例とも5年生きることが確実でもない限り、この値は妥当ではありません。これは本当の死亡率よりは低すぎることになり、むしろその下限を表わしています。
つまり、通常は打ち切り例を完全な生存例や死亡例として扱うわけにはいきません。かといって、「つい1週間前に観察を開始した」というわけでもない限り、始めから無視するわけにもいきません。「少なくともある期間は生きている」という事実があるからです。もし、この2例を無視して死亡率を $\frac{5}{5+3}$ とすると、この推定値はまだ多少死亡率を高く見積るおそれがあります。
もし、打ち切り例を最初からなかったものとして厄介払いするならば、時計の針を5年前に戻して、それ以後に手術した全例(死亡の5例の中で最近5年未満に手術した症例も含めて)を除外しなければなりません(これを直接法による生存率と呼びます)。これは堅実な方法のこともありますが、観察期間の短い症例を無駄にすることになります。
生存の解析に当たって、途中で追跡ができなくなった対象者を全経過生存したものとして扱うと、追跡ができなくなった時点以降に発生したかもしれない死亡も生存扱いして死亡率(死亡の発生速度)が低く算定され、反対に途中で追跡ができなくなった対象者を解析から完全に外してしまうと、追跡できていた時点までの生存が無視されて死亡率を高く見積もってしまいます。このように、打ち切り例の取り扱い方しだいでは、結果にバイアスがかかってしまう可能性があります。
こうした問題があるため、生存時間分析では、「観察が打ち切られるまでは生存していた」、「イベントが発生するのは、少なくとも打ち切りよりも後である」といった情報を活かした特別な考え方が必要となります。
ハザード
定義
「観察が打ち切られるまでは生存していた」という情報を最大限活かすことのできる指標がハザードと呼ばれる指標です。ハザードhazard とは、ある時点 $t$ まで生存していた個体に対する、極めて短い単位時間 $\Delta t$ あたりの平均死亡確率であり、数学的には \begin{align} h \left(t\right)=\lim_{\Delta t\rightarrow0}{\frac{P \left(\ t \le T \lt t+\Delta t\ \middle|\ t \le T\ \right)}{\Delta t}} \end{align} と定義されます。 ハザードは、瞬間死亡率とも呼ばれ、発生率や死亡率と呼ばれる疫学指標に対応する指標です。
上の定義だけを見ると、その意味が非常につかみにくいところですが、大雑把にいえば、「今日○○歳の誕生日を迎えた自分が、今後1年間で死亡してしまう確率はどれくらいか?」という質問と同じタイプの情報をもっており、ある区間の瞬間的なイベントの発生確率に注目しています。似たイメージをもつ例として、自動車の走行速度を挙げることができます。自動車でどこかに行く場合、時速60 km/h で走ろうと思っていても、アクセルの微妙な踏み込み具合に応じて、59.9 km/h になったり、60.2 km/h になったりすることがありますが、この時々刻々移り変わる、その瞬間の速度が発生率や死亡率のイメージです。
ハザードは本質的に「率」なので、理論的に取り得る値の範囲は、「0以上の値すべて」であり、「割合」とは異なり、分子の単位を分母の単位で除した単位をつけて表記します。 \begin{align} h \left(t\right) \left[/\mathrm{time}\right]\in \left[0,\infty\right] \end{align} また、生存関数などとは異なり、必ずしも1で始まる必要はなく、「非負の関数」という制限しかありません。
ハザード関数
ハザードの身近な例は、先ほども出てきた簡易生命表の死亡率です。表5では男女別の死亡率を0 歳から10 歳刻みで示しており、各年齢の死亡率の推移を図2に示しています。このように、縦軸にハザード、横軸に経過時間をとったものをハザード関数 hazard function と呼びます。
| 年齢 | 男性 | 女性 |
|---|---|---|
| $0$ | $0.0018$ | $0.0016$ |
| $10$ | $0.0001$ | $0.0001$ |
| $20$ | $0.0004$ | $0.0002$ |
| $30$ | $0.0005$ | $0.0003$ |
| $40$ | $0.0009$ | $0.0006$ |
| $50$ | $0.0024$ | $0.0014$ |
| $60$ | $0.0063$ | $0.0028$ |
| $70$ | $0.0168$ | $0.0068$ |
| $80$ | $0.0450$ | $0.0214$ |
| $90$ | $0.1440$ | $0.0901$ |
| $100$ | $0.3696$ | $0.2978$ |

簡易生命表では、各年齢の1年間あたりの死亡率が示されていますが、これがほぼハザードに相当します。簡易生命表では、死亡率は、ちょうど $x$ 歳に達した者が $x+n$ 歳に達しないで死亡する確率
と定義されていて、例えば、「60 歳死亡率」とは、ちょうど60 歳に達した人が、次の1年間で61歳に達する前に死亡する確率を表しています。先の説明の中で出てきた「瞬間」や「極めて短い単位時間」が簡易生命表では、$∆t=1$ 年として計算しているということです。これらの図表を見ると、日本人の死亡ハザードは、明らかに年齢とともに異なっており、時間の関数となっていることが分かります。
死亡率のおおまかな推移を見ると、出生直後が若干高く、その後40歳くらいまで低い値で安定し、40歳を過ぎると、右肩上がりに上昇しています。出生直後が若干高くなっているのは、0歳では出産直後の死亡や乳幼児死亡が発生するためです。乳幼児であっても、がんや心疾患を発症する場合があるほか、感染症などに罹患した場合、免疫機能が未発達であるために亡くなってしまう確率が高くなってしまいます。この傾向は、身体機能の成長と共に解消されていき、やがて低い水準での安定期に入ります。
その後、40歳くらいまでは、事故などの偶発的な要因が死因の上位を占め、疾病による死亡が非常に少なくなります。これに対し40歳以降は、年齢とともに急激にハザードが上昇します。これは、悪性新生物、心疾患、脳血管疾思による死亡が増大するためで、年齢の経過とともに体のいたるところに疾患が生じ、それが死の原因となります。
こうしたハザード関数の形状は、その形からバスタブ曲線 bathtub curve とも呼ばれています。この言葉はもともと工学で用いられていた言葉で、初期故障期 early failure period, infant mortality、偶発故障期 intrinsic failure period, useful life、摩耗故障期 wear-out failure period の3つの時期から構成されています。
ハザードを考える意義
ハザードは、最も単純な場合、人・時法によって求めることができます。例えば、表4のデータの場合、5年生存率は正確には分からなくても、5年経過時点における死亡ハザード(発生率)は、 \begin{align} h \left(5\right)=\frac{5}{1.1+1.5+2.3+ \cdots +5+5}=\frac{5}{34.3}=0.146 \left[/\mathrm{P \cdot Y}\right] \end{align} と求めることができます。 ハザードは、観測の起点から観察が完了する(打ち切りも含む)までの情報のみを必要とし、観測を終えた後の情報については必要としないため、どのような場合でも必ず算出することができるという点に利点があります。
ただ、人・時法によるハザードの算出・比較は理解しやすく計算も簡単ですが、その方法が妥当であるためには、発生率が観察期間を通して一定であるという条件が必要となります。この条件が成立している場合、人・時法による発生率の逆数は、「合計観察時間/発生数」なので、イベント発生までの平均的な時間として解釈できます。
しかしながら、人・時法で必要な条件「発生率は観察期間を通して変化しない」は研究開始から1年たっても5年たっても発生率は同じであることを要求しており、かなり厳しい仮定です。この仮定が満たされないと思われる場合には、観察期間を発生率が一定とみなせる期間に区切って比較を行う必要があります。
いっぽう、上の条件を緩めて「発生率は時間とともに変化してもかまわない」とすると、発生率は時々刻々と変化するので、もはや人・時法のような安定した推定値を得ることはできなくなります。そのため臨床研究の場では、人・時法によるハザードの推定があまり行われず、カプラン・マイヤー法などを用いて生存関数を直接的に推定します。
しかし、カプラン・マイヤー法などの手法も、原理的にはハザードを用いて計算を行っており、次節で紹介する指標同士の関係が理論的な背景となっています。
指標同士の関係
生存関数、ハザード関数、死亡密度関数の関係
ここからはやや数学的な話になりますが、ハザードの定義式を変形すると以下のような関係式が得られます。 \begin{align} h \left(t\right)&=\lim_{\Delta t\rightarrow0}{\frac{P \left(\ t \le T \lt t+\Delta t\ \middle|\ t \le T\ \right)}{\Delta t}}\\ &=\lim_{\Delta t\rightarrow0}{\frac{1}{\Delta t} \cdot \frac{S \left(t\right)-S \left(t+\Delta t\right)}{S \left(t\right)}}\\ &=\frac{1}{S \left(t\right)} \cdot \lim_{\Delta t\rightarrow0}{\frac{ \left\{1-F \left(t\right)\right\}- \left\{1-F \left(t+\Delta t\right)\right\}}{\Delta t}}\\ &=\frac{1}{S \left(t\right)} \cdot \lim_{\Delta t\rightarrow0}{\frac{F \left(t+\Delta t\right)-F \left(t\right)}{\Delta t}}\\ &=\frac{f \left(t\right)}{S \left(t\right)} \end{align} したがって、 \begin{gather} f \left(t\right)=S \left(t\right) \cdot h \left(t\right)\\ P \left(T=t\right)=P \left(t \le T\right) \cdot P \left(T=t\middle| t \le T\right) \end{gather} これは、生存関数、ハザード関数、死亡密度関数の関係を表していて、「ある時点 $t$ にイベントを発生する確率」は「ある時点 $t$ まで生存する確率」と「ある時点 $t$ まで生存したという条件の下で、時点 $t$ の瞬間にイベントが発生する確率」の積として求められるという関係です。
生存関数、ハザード関数、累積ハザード関数の関係
また、ハザード関数の定義式は以下のようにも変形することができます。 \begin{align} h \left(t\right)&=\lim_{\Delta t\rightarrow0}{\frac{P \left(\ t \le T \lt t+\Delta t\ \middle|\ t \le T\ \right)}{\Delta t}}\\ &=\lim_{\Delta t\rightarrow0}{\frac{1}{\Delta t}} \cdot \frac{S \left(t\right)-S \left(t+\Delta t\right)}{S \left(t\right)}\\ &=\lim_{\Delta t\rightarrow0}{\frac{S \left(t\right)-S \left(t+\Delta t\right)}{\Delta t}} \cdot \frac{1}{S \left(t\right)}\\ &=\frac{1}{S \left(t\right)} \cdot \lim_{\Delta t\rightarrow0}{\frac{S \left(t\right)-S \left(t+\Delta t\right)}{\Delta t}}\\ &=\frac{1}{S \left(t\right)} \cdot \left\{-\lim_{\Delta t\rightarrow0}{\frac{S \left(t+\Delta t\right)-S \left(t\right)}{\Delta t}}\right\}\\ &=-\frac{dS \left(t\right)}{dt} \cdot \frac{1}{S \left(t\right)}\\ &=-\frac{d}{dt}\log{S \left(t\right)}\tag{1} \end{align}
ここで、累積ハザード関数 cumulative hazard function を以下のように定義します。 \begin{gather} H \left(t\right)=\int_{0}^{t}h \left(u\right)du\tag{2} \end{gather}
このとき、式 $(1),(2)$ より、 \begin{align} H \left(t\right)&=\int_{0}^{t}{-\frac{d}{du}\log{S \left(u\right)}du}\\ &= \left[-\log{S \left(u\right)}\right]_0^t\\ &=-\log{S \left(t\right)}+\log{S \left(0\right)}\\ &=-\log{S \left(t\right)}+\log{1}\\ &=-\log{S \left(t\right)} \end{align} したがって、 \begin{gather} \log{S \left(t\right)}=-H \left(t\right)\tag{3}\\ S \left(t\right)=\exp \left\{-H \left(t\right)\right\}\tag{4} \end{gather}
式 $(1) \sim (4)$ は、生存関数、ハザード関数、累積ハザード関数のうちどれか1つが決まれば、残りの2つも自動的に決まるという意味で数学的には等価なものであることを示しています。
ただし、この3種は「統計的なデータ解析」を行う上では等価ではありません。ちょうど自動車の瞬間速度の測定が到達距離に比べ困難であるように、ハザード関数の推定は確率的な誤差の影響を受けやすく、いっぽう、一種の平滑化のため、生存関数の推定は相対的には安定しています。国の人口データのような大規模データを対象とする場合には、人年法によってハザードを直接的に推定できますが、比較的粗なデータを扱う臨床研究においては、カプラン・マイヤー法などによって、より安定した生存関数の方を推定します。
累積ハザード関数
前節で累積ハザード関数を定義しましたが、最後にその意味やイメージについて考えてみたいと思います。定義式を言葉にすれば、観測開始からある時点 $t$ まで、ハザードを加算(積分)した値ということになります。この値の意味はすぐには分かりませんが、イメージとしては、「蓄積ダメージ」、あるいは、自動車にたとえれば、「これまでの走行距離」などに近いと思われます。あなたは自動車に乗っていて、どれくらいの距離かは分かりませんが、事前に定められた距離に到達したら、その時点で車が壊れてしまいます。走行中はアクセルの踏み込み具合によって、30 km/h のときもあれば、100 km/h のときもあり、瞬間的な速度はいろいろ変化するものの、時間の経過とともに確実に距離は伸びていき、終了地点に近づいていきます。これと同様に、人は人生の中で夜更かしをしたり、運動不足の日々が続いたり、ストレスを感じたりして、死亡リスクが高まるとき(踏み込みが深くなる瞬間)があり、逆に、趣味に没頭したり、運動をしたり、みんなと気晴らしをしたりして、健康的になるとき(踏み込みが浅くなる瞬間)もあります。
累積ハザード関数は非負の値しかとらないハザードを積分するので、単調増加(正確にいうと単調非減少)関数になります。ハザード関数が大きな値をとるほど死亡のリスクが高くなり、生存関数は速く0に近づきます。例えばある処置を施すことによって、どの時点でもハザード関数が $a$ 倍になるとすると、 \begin{gather} h_a \left(t\right)=a \cdot h \left(t\right) \end{gather} 生存関数とハザード関数の関係より、 \begin{align} S_a \left(t\right)&=\exp \left\{-\int_{0}^{t}{h_a \left(t\right)du}\right\}\\ &=\exp \left\{-\int_{0}^{t}{a \cdot h \left(t\right)du}\right\}\\ &=\exp \left\{-a\int_{0}^{t}h \left(t\right)du\right\}\\ &= \left[\exp \left\{-\int_{0}^{t}h \left(t\right)du\right\}\right]^a\\ &= \left[S \left(t\right)\right]^a \end{align} となります。 すなわち、ハザードで $a$ 倍のリスクの上昇は生存関数では $a$ 乗の形で効いてくることがわります。生存関数は0から1の間の値をとるので、$a$ が正(リスクが上がる)であれば、生存関数は $a$ 乗されて小さくなります(速く0に近づく)。
例えば時点 $a$ における元の生存関数の値を0.8とすると、ハザードが2倍になると $S_a \left(t\right)$ は0.64となり、ハザードが4倍になると0.41になります。ハザードが2倍というと随分リスクが上がったような印象を受けますが、生存関数では0.8が0.64になるだけです。基準の生存割合が大きい場合、我々が直観的に理解しやすい生存関数の変化と比べて、ハザード関数の変化の方が大きく感じられるので注意が必要となります。
参考文献
- 大橋 靖雄, 浜田 知久馬 著. 生存時間解析:SASによる生物統計. 東京大学出版会, 1995, p.1-21
- 前谷 俊三 著. 臨床生存分析:生存データと予後因子の解析. 南江堂, 1996, p.2-10, p.18-19
- 中村 剛 著. Cox比例ハザードモデル. 朝倉書店, 2001, p.1-9
- 浜田 知久馬 著. 学会・論文発表のための統計学:統計パッケージを誤用しないために. 真興交易医書出版部, 2012, p.212-218
- デビッド・ホスマー, スタンリー・レメショウ, スーザン・メイ 著, 五所 正彦 監訳. 生存時間解析入門. 東京大学出版会, 2014, p.1-11
- 西川 正子 著. カプラン・マイヤー法:生存時間解析の基本手法. 共立出版, 2019, p.1-14
- 赤澤 宏平. 生存時間データの解析. 医療情報学. 2001, 20(6), p.451-461, doi: 10.14948/jami.20.451
- Clark, T.G., Bradburn, M.J., Love, S.B. et al.. Survival analysis part I: basic concepts and first analyses. Br J Cancer. 2003, 89(2), p.232-238, doi: 10.1038/sj.bjc.6601118
- Bradburn, M.J., Clark, T.G., Love, S.B. et al.. Survival analysis part II: multivariate data analysis-an introduction to concepts and methods. Br J Cancer. 2003, 89(3), p.431-436, doi: 10.1038/sj.bjc.6601119
- 浦島 充佳. 生存分析の基本と読みかた. 小児科診療. 2009, 72(4), p.707-713.
- 山本 精一郎. がん臨床試験の生物統計学. 産科と婦人科. 2010, 77(5), p.495-502.
- 山口 拓洋. 有効性評価:生存曲線から何を読み取るの?. 月刊薬事. 2012, 54(13), p.2141-2145.
- 松山 裕. 生存時間解析. 心身医学. 2013, 53(11), p.1031-1038, doi: 10.15064/jjpm.53.11_1031
- 藤田 烈. 疫学・統計解析シリーズ:生存時間解析結果を読み解くための基礎知識. 日本環境感染学会誌. 2014, 29(5), p.313-323, doi: 10.4058/jsei.29.313
- George, B., Seals, S. & Aban, I.. Survival analysis and regression models. J Nucl Cardiol. 2014, 21(4), p.686-694, doi: 10.1007/s12350-014-9908-2
引用文献
- 厚生労働省. 令和3年簡易生命表. 2022, https://www.mhlw.go.jp/toukei/saikin/hw/life/life21/index.html.



0 件のコメント:
コメントを投稿