生存関数の推定

生存時間データの分析は、生存関数の推定によって始まります。本稿では、生存関数のパラメトリックモデルを概観した後、ノンパラメトリックな推定方法、特に、カプラン・マイヤー法による推定方法の進め方やグリーンウッドの公式、ネルソン・アーレン推定量などについて解説しています。

なお、閲覧にあたっては、以下の点にご注意ください。

• スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
• 特に断りがない限り、打ち切りは、「情報のない右側打ち切り」のことを指します。

 

生存時間データの記述法

他の医学・疫学研究と同様、生存時間データを取り終わり、解析段階に入ったときにまずするべきことは、いわゆる「データの記述」です。しかし、生存時間データには、「打ち切りデータがある場合、平均や分散を求めることができない」という特徴があるため、そうした指標の算出は飛ばして、代わりに、生存関数を推定することによって、時間の経過とともに、累積生存率がどのように推移していくのかを把握することが分析の第1歩となります。

生存関数の推定方法

生存関数の推定方法には、大きく分けて、パラメトリックな方法とノンパラメトリックな方法の2種類があります。

パラメトリックな方法とは、生存時間の分布が特定の分布に従うと仮定し、その特定の分布のパラメータを推定するという方法です。この方法は、過去の研究から生存時間に対して特定の分布を想定できる場合に用いられる方法で、①パラメータの値を推定できれば生存率曲線が完全に再現できる、②通常は、実際の観察期間内のことしか分からないが、分布のモデル式が明らかになっていれば、最長観察期間を越えた先のことまで予測できるなどの利点があります。具体的には、指数分布モデル、ワイブル分布モデル、加速死亡時間モデルなどのモデルがあります。

これに対し、ノンパラメトリックな方法とは、生存時間の分布が特定の分布に従うと仮定せず、各時点の累積生存率をデータから直接的に推定するという方法で、生存時間の分布について参照できる情報がない場合に用いられます。具体的には、カプラン・マイヤー法や生命表法などの手法があります。

これら2種類の方法のうち、パラメトリックな方法によって推定できるのが理想ではありますが、実際には、特定のモデルを想定できる場合は少なく、特に仮定を必要としないノンパラメトリックな方法を用いるのが一般的とされ、医学研究では、特にカプラン・マイヤー法が生存時間分析の標準的な解析方法として定着しています。そのため本稿では、次節でパラメトリックな方法の概要を見た後、カプラン・マイヤー法について詳しく解説していきます。

 

生存関数のパラメトリックモデル

指数分布モデル

指数分布モデル exponential distribution model は、生存時間が指数分布に従うと仮定するモデルです。パラメータは、スケール・パラメータ $\lambda$ が1つだけの最もシンプルなモデルです。生存関数やハザード関数などは、 \begin{gather} h \left(t\right)=\lambda \quad H \left(t\right)=\lambda t\\ S \left(t\right)=e^{-\lambda t}\\ f \left(t\right)=\lambda e^{-\lambda t} \quad F \left(t\right)=1-e^{-\lambda t}\\ 0 \lt \lambda \end{gather} また、指数分布の期待値と分散の公式より、平均生存時間と生存時間中央値は、それぞれ \begin{gather} E \left(T\right)=\frac{1}{\lambda} \quad \mathrm{MST}=\frac{\log{2}}{\lambda} \end{gather} となります。

指数分布モデルの特徴は、ハザード関数が時間に依らない定数 $\lambda$ である点にあり、ある時間まで生存した人が、その後平均してどれだけ生存できるかは、これまで生きた時間と無関係であるという点にあります。これは、指数分布の無記憶性 memory-less、すなわち、 \begin{gather} P \left(t \lt T\right)=P \left(t+t_0 \lt T\middle| t_0 \lt T\right) \end{gather} という性質を反映しています。

実際的な意味としては、経過時間にかかわらず、イベントが偶発的に起こるということを表していて、信頼性工学の言葉ではこの型の故障を偶発故障型と呼びます。

ハザード曲線は定数なので、経過時間の軸と平行な直線となります。経過時間によってイベントの起こりやすさが変わらないので、イベントの絶対数は最初のうちが最も多く、後ほど少なくなります。このため、死亡密度関数は、最初が最も高く、時間とともに尻下がりになります（単調減少な関数）。生存率曲線もこれを反映し、最初に最も急な勾配で下降します。

指数分布モデルはいつイベントが発生しても不思議がないような相当進行した患者や重症例には当てはまりますが、すぐにはイベントが起こらない早期癌や軽症例には当てはまりにくくなります。

ワイブル分布モデル

ワイブル分布モデル Weibull distribution model は、生存時間がワイブル分布に従うと仮定するモデルであり、応用上最もよく用いられる生存時間分布です。パラメータは、スケール・パラメータ $\mu$ と形状パラメータ $\gamma$ の2つだけの最もシンプルなモデルです。生存関数やハザード関数などは、 \begin{gather} h \left(t\right)=\mu\gamma t^{\gamma-1} \quad H \left(t\right)=\mu t^\gamma\\ S \left(t\right)=\exp \left(-\mu t^\gamma\right)\\ f \left(t\right)=\mu\gamma t^{\gamma-1} \cdot \exp \left(-\mu t^\gamma\right) \quad F \left(t\right)=1-\exp \left(-\mu t^\gamma\right)\\ 0 \lt \mu \quad 0 \lt \gamma \end{gather} となります。

この分布はハザード関数が時間 $t$ のベキ関数であらわされる分布であり、ベキ次数をどのように設定するかによってハザード関数の形状が大きく変化します。$\gamma=1$ とおくとハザード関数が定数となり、ワイブル分布は指数分布に帰着します。

$1 \lt \gamma$ の場合、ハザードは時間とともに段々増加します。このような場合を摩耗故障型といい、人間の成年期を過ぎた後の死亡は摩耗型であり、年齢とともに死亡のハザードが増えてきます。

$0 \lt \gamma \lt 1$ の場合、ハザードは時間とともに段々減少します。このような場合を初期故障型といい、人間の死亡のハザード関数は、最初は乳幼児死亡率がかなり高く初期故障型であり、青年期ではハザードは一定になり、最後は摩耗型のハザード関数になります。

 

ノンパラメトリックな生存関数の推定

ノンパラメトリックな生存関数の推定方法には、大きく分けて2 種類の方法があります。1つは、古典的な生命表法 life table method、または生命保険数理法 actuarial method と呼ばれる推定方法、もう1つは、カプラン・マイヤー法 Kaplan-Meier method です。

生命保険数理法は、手計算で生存関数が推定できる簡便な方法ですが、同時に推定の精度が低く、ざっくりとした方法である点に難があります。以前は、計算の煩雑さが問題となっていましたが、近年はコンピューターが普及し、計算の手間が問題とならなくなったため、より推定精度の高いカプラン・マイヤー法が標準的な解析方法として定着しています。

連続的な生存時間を考えることのできるパラメトリックな方法とは異なり、ノンパラメトリックな方法は、いずれも生存時間を離散型確率変数として扱い、特定の時点における生存関数をピンポイントに推定する方法です。

カプラン・マイヤー法

記号の定義

では、カプラン・マイヤー法$^\mathrm{(1)}$による生存関数の推定方法を見ていきます。まず、例えばあなたはあるがんの治療薬の効果を調べるために、全部で $N$ 人の人を追跡し、研究期間終了までに $J \left( \le N\right)$ 個のイベントが発生し、$N-J$ 個の観察が打ち切られたとします。

研究期間が終了したら、まずは、観察時間の算出と並び替えを行います。実験研究のように、開始時間がすべての観察対象で同じである場合は分かりやすいですが、臨床研究において、登録時期がバラバラである場合は、例えば、Excel上で「観察終了日」から「観察開始日」を引くことによって、観察開始時点を0として観察できた生存時間を算出します。

一般的には、例えば被験者番号を $k \left(=1,2, \cdots ,N\right)$ とすると、観察時間 $t_k$ とイベント発生状況を表す指示変数 $\delta_k$ のデータの組 $ \left(t_k,\delta_k\right)$ が得られていますが、このうち、観察時間 $t_k$ を昇順、すなわち、 \begin{gather} t_{ \left(1\right)} \le t_{ \left(2\right)} \le \cdots t_{ \left(N\right)} \end{gather} というふうに並び替えます。 このとき、$t_{ \left(k\right)}$ には、イベントが発生したデータ（$\delta_{ \left(k\right)}=1$）と打ち切りデータ（$\delta_{ \left(k\right)}=0$）が混在しています。このようなデータを整理する方法には、①イベント発生時点のみに着目する方法と②すべての観察終了時点（＝イベント発生と打ち切り）に着目する方法などの方法がありますが、最終的な結論は同じになるので、本稿では、よく用いられている①の方法で整理するものとします。

すなわち、$J$ 個のイベント発生時点を抜き出し、値が小さいものから順に、新たに番号 $t_j$ を振り、 \begin{gather} 0=t_0 \lt t_1 \le t_2 \le \cdots t_J \end{gather} とします。 このとき、時点 $t_j$ でのイベント発生数を \begin{gather} d_j \left( \gt 0\right) \end{gather} 時点 $t_j$ と時点 $t_{j+1}$ の間に発生した打ち切り数を \begin{gather} w_j \left( \geq 0\right) \end{gather} とします。

また、カプラン・マイヤー法においては、各時点でのリスク集合の大きさを考える必要があります。リスク集合の大きさ population at risk とは、他の研究分野で用いられるのと同様、新たにイベントの発生が観察される可能性がある個体の数を意味します。この記法においては、 \begin{gather} n_j=n_{j-1}-d_{j-1}-w_{j-1}\\ n_0=N \quad d_0=0 \end{gather} と定義されます。 なお、イベントの発生と打ち切りが同時点で発生した場合、慣例的に、イベントが発生した後に打ち切りが発生したとみなし、打ち切りをその時点のリスクの集合に含めて計算を行い、その後、リスク集合から取り除きます。

このときデータは、以下のように書けます。

 

表1 カプラン・マイヤー法における生存時間データ

時点 $t_j$	イベント数 $d_j$	打ち切り数 $w_j$	リスク集合 $n_j$
$t_0=0$	$d_0=0$	$-$	$n_0=N$
$\vdots$	$\vdots$	$w_0$	$-$
$t_1$	$d_1$	$-$	$n_1=N-w_0$
$\vdots$	$\vdots$	$w_1$	$-$
$t_2$	$d_2$	$-$	$n_2=n_1-d_1-w_1$
$\vdots$	$\vdots$	$\vdots$	$\vdots$
$t_j$	$d_j$	$-$	$n_j=n_{j-1}-d_{j-1}-w_{j-1}$
$\vdots$	$\vdots$	$w_j$	$-$
$t_{j+1}$	$d_{j+1}$	$-$	$n_{j+1}=n_j-d_j-w_j$
$\vdots$	$\vdots$	$\vdots$	$\vdots$
$t_J$	$d_J$	$-$	$n_J=n_{J-1}-d_{J-1}$

カプラン・マイヤー法に必要な仮定

カプラン・マイヤー法を用いる際には、いくつかの仮定が必要となります。

1つ目の仮定は、先にスタートした人もあとにスタートした人も同じイベント発現パターンを示すことです。先述のように、実際の観察においては観察開始日が異なりますが、そうしたカレンダー上の時点ではなく、あくまでも観察開始からの経過時間に応じて、イベントが発生する必要があるということです。

2つ目の仮定は、打ち切りが情報のない打ち切りであることです。これはすなわち、「観察が打ち切られた対象者は、その後観察が続けられていれば、打ち切られずに観察された対象者と同じ確率でイベントが発生する」という仮定です。この仮定にもとづき、打ち切り例は打ち切りが発生した時点以降は解析から除外して、生存にも死亡（イベント発生）にもカウントしないという手続きとります。

カプラン・マイヤー推定量

結論を先に述べると、$t_j \le t \lt t_{j+1}$ を満たす $t$ に対し、カプラン・マイヤー法による累積生存率の推定量は、 \begin{gather} \hat{S} \left(t\right)=\prod_{i=1}^{j}\frac{n_i-d_i}{n_i} \end{gather} で推定されます このカプラン・マイヤー法による累積生存率の推定量は、そのままカプラン・マイヤー推定量 Kaplan-Meier estimator と呼ばれます。

ここで、カプラン・マイヤー推定量の意味を考えてみましょう。$n_j$ は時点 $t_j$ におけるリスク集合の大きさ、$d_j$ はイベント発生数、$n_j-d_j$ は時点 $t_j \le t \lt t_{j+1}$ における生存者数を表しています。つまり、 \begin{gather} p_i=\frac{n_i-d_i}{n_i} \end{gather} は、 時点 $t_i$ の直前で生存していた個体のうち、時点 $t_i$ を乗り越えて生存できる個体の割合、ある人が時点 $t_i$ の直前で生存しているという条件の下で、時点 $t_i$ を乗り越えて生存できる確率を表していることが分かります。そして、その条件付き確率の時点 $t_j$ までの積が時点 $t_j$ における累積生存率の推定値だと言っています。この意味で、提唱者であるカプラン・マイヤーは当初、この推定方法のことを積・極限法 product-limit と呼んでいました。

 

条件付き確率としての累積生存率

カプラン・マイヤー推定量は条件付き確率の積として表されますが、このことは、次のようにイメージすることができると思います。例えば、人々の生死を意のままに操れる超越的な存在がいて、観測対象としている人々のイベント発生のタイミングは、実はその存在によって決められているとしましょう。その存在は、あらかじめ研究期間中のイベント発生の総数とタイミングを決めていて、予定していたタイミングが訪れる度に、各人の名前が記されたくじを非復元抽出で引き、そこに名前が書かれていた人にイベントを発生させます。

打ち切りがない場合

例えば、以下のように $N=10$ として、1日目から10日目まで毎日1人ずつくじを引かれていくとします。まず、打ち切りがない場合を考えます。

表2 仮想的な生存時間データ（打ち切りがない場合）

時点 $t_j$	イベント数 $d_j$	当選者番号 $i$	生存者数 $n_j$
$t_0=0$	$d_0=0$	$-$	$10$
$t_1=1$	$d_1=1$	$?$	$9$
$t_2=2$	$d_2=1$	$?$	$8$
$t_3=3$	$d_3=1$	$?$	$7$
$t_4=4$	$d_4=1$	$?$	$6$
$t_5=5$	$d_5=1$	$?$	$5$
$t_6=6$	$d_6=1$	$?$	$4$
$t_7=7$	$d_7=1$	$?$	$3$
$t_8=8$	$d_8=1$	$?$	$2$
$t_9=9$	$d_9=1$	$?$	$1$
$t_{10}=10$	$d_{10}=1$	$?$	$0$

このとき、巻き込まれたあなたが1日目の危機を乗り越えられる確率と見事「当選」してしまう確率は、それぞれ \begin{gather} p_1=\frac{9}{10} \quad q_1=\frac{1}{10} \end{gather} となります。

続いて、2日目の危機を乗り越えたいところですが、そのためには、まず1日目の試練を乗り越えることが最低条件となります。したがって、2日目の生存・死亡確率はそれぞれ、 \begin{gather} p_1=\frac{9}{10} \cdot \frac{8}{9}=\frac{4}{5} \quad q_1=\frac{1}{9} \end{gather} となります。 以下、これが順繰りに繰り返されていき、最終日には、最後の1人の名前が確定的に引かれて終了となります。

打ち切りがある場合

打ち切りがある場合も、ほぼ同様に考えることができます。この場合、全部で $J$ 個のイベント枠の時点が用意されるとともに、$N-J$ 個の打ち切り枠の時点が用意されます。打ち切り枠で選ばれた人がその後どうなるかは分かりませんが、選ばれる人は超越者があらかじめ決めています。参加者は、自分が打ち切り枠であるかどうかは分からず、打ち切り枠の時点を迎えたときに、それが誰だったかが発表され、発表後、抽選用の名簿から打ち切り枠の人の名前が除外されます。

先ほどと同様に、$N=10$ として、毎日1人ずつくじを引かれていき、あらかじめ、3日目、7日目、9日目に打ち切り枠が設定されました。

表3 仮想的な生存時間データ（打ち切りがある場合）

時点 $t_j$	イベント数 $d_j$	当選者番号 $i$	リスク集合 $n_j$
$t_0=0$	$d_0=0$	$-$	$10$
$t_1=1$	$d_1=1$	$?$	$9$
$t_2=2$	$d_2=1$	$?$	$8$
$t_{2.5}=3$	$d_3=0$	$?$	$7$
$t_3=4$	$d_4=1$	$?$	$6$
$t_4=5$	$d_5=1$	$?$	$5$
$t_5=6$	$d_6=1$	$?$	$4$
$t_{5.5}=7$	$d_7=0$	$?$	$3$
$t_6=8$	$d_8=1$	$?$	$2$
$t_{6.5}=9$	$d_9=0$	$?$	$1$
$t_7=10$	$d_{10}=1$	$?$	$0$

このとき、あなたが2日目に生き残っている確率は、先ほどと同様に \begin{gather} p_2=\frac{4}{5} \end{gather}

続いて、3日目 $t_{2.5}$ で打ち切り枠が発表されましたが、それは自分ではありませんでした。このとき、あなたに分かるのは、「次の抽選は4日目で、それ以外に死ぬことはないから今日1日の生存が確定する」、すなわち、 \begin{gather} p_{2.5}=\frac{8}{10} \quad q_{2.5}=0 \end{gather} ということです。 また、「打ち切り枠の人が名簿から除外されたので、次の抽選時に名前を引かれる確率が上がった」ということも分かります。

このことから、4日目 $t_3$ に生き残っている確率は、 \begin{gather} p_3=\frac{4}{5} \cdot \frac{6}{7}=\frac{24}{35} \quad q_3=\frac{1}{7} \end{gather}

以下、同様に考えていくと、生存関数と生存曲線は以下のようにまとめることができます。

表4 仮想的な生存時間データ（打ち切りがある場合） まとめ

時点 $t_j$	リスク集合 $n_j$	死亡数 $d_j$	死亡率 $q_j$	生存率 $p_j$	累積生存率 $\hat{S} \left(t_j\right)$	打ち切り数 $w_j$
$t_0$	$10$	$0$	$0$	$1$	$1$	$0$
$t_1$	$10$	$1$	$\frac{1}{10}$	$\frac{9}{10}$	$\frac{9}{10}$	$0$
$t_2$	$9$	$1$	$\frac{1}{9}$	$\frac{8}{9}$	$\frac{4}{5}$	$1$
$t_3$	$7$	$1$	$\frac{1}{7}$	$\frac{6}{7}$	$\frac{24}{35}$	$0$
$t_4$	$6$	$1$	$\frac{1}{6}$	$\frac{5}{6}$	$\frac{4}{7}$	$0$
$t_5$	$5$	$1$	$\frac{1}{5}$	$\frac{4}{5}$	$\frac{16}{35}$	$1$
$t_6$	$3$	$1$	$\frac{1}{3}$	$\frac{2}{3}$	$\frac{32}{105}$	$1$
$t_7$	$1$	$1$	$1$	$1$	$0$	$0$

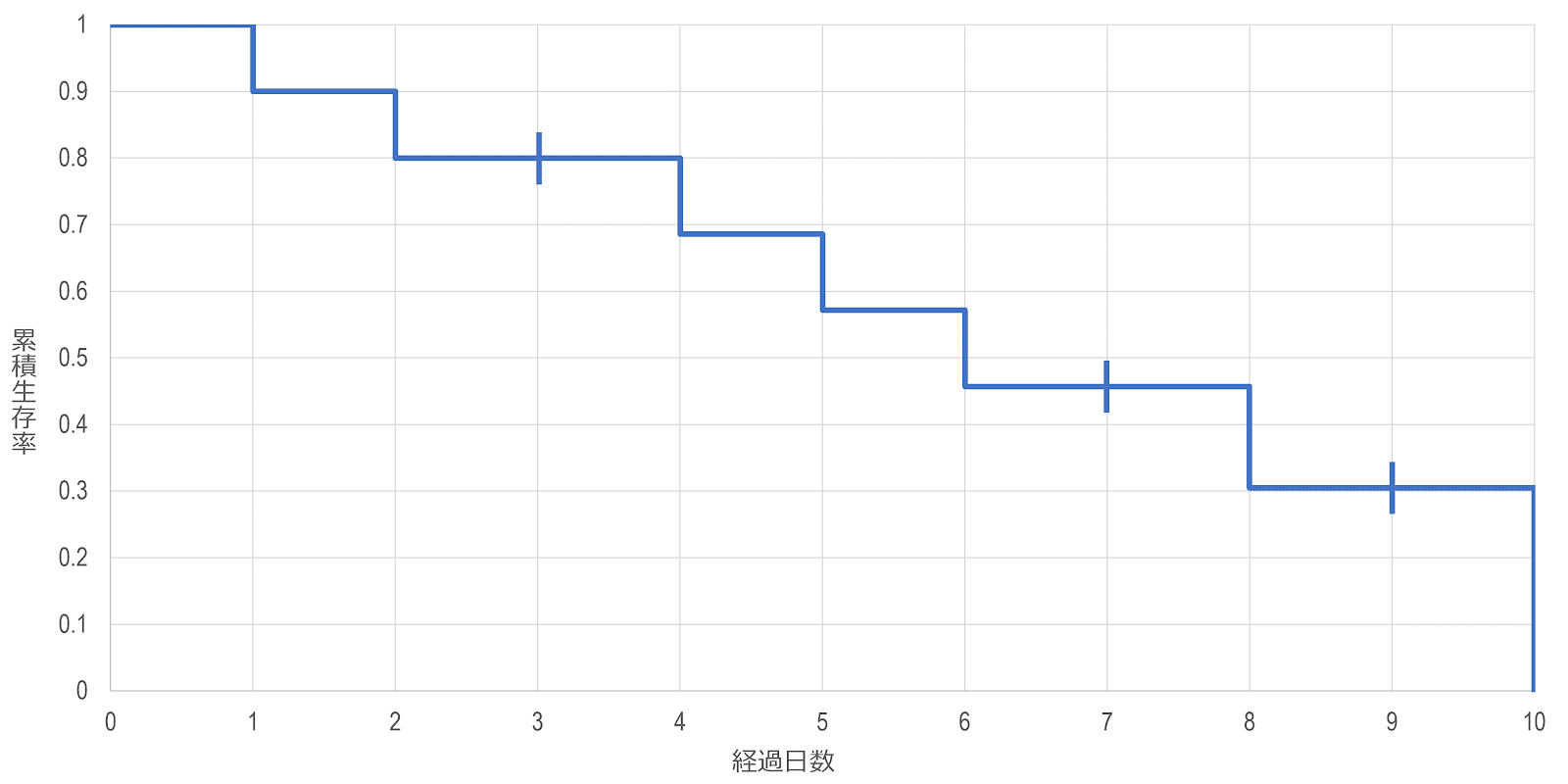
このように、カプラン・マイヤー法によって推定された生存曲線をカプラン・マイヤー曲線 Kaplan-Meier curveと呼び、打ち切りが発生した時点にしるしをつけることがあります。カプラン・マイヤー曲線は、上に示したように、打ち切りが発生した時点では変化せず、イベントが発生する度に垂直に降下する階段型のグラフとなります。基本的なルールとして、次のイベントが発生するまでは累積生存率は一定という仮定があるため、打ち切りには影響を受けず、各時点の累積生存率を単純につなぐ折れ線型グラフとしては描きません。

カプラン・マイヤー曲線は経過時間に比例して、段差の大きさが大きくなっていきます。これは、観察が終了される度にリスク集合が小さくなり、実際に追跡を継続している対象者1人あたりの重みが増し、1人のイベント発生が大きく扱われるためです。

カプラン・マイヤー推定量は、打ち切り例が存在するため、狭義での累積生存率、すなわち「全体のうち、ある時点 $t$ を超えて生存する個体の割合」とは意味が少し異なり、ある個体が時点 $t$ を超えて生存する確率という意味になります。

 

離散型変数のハザード

本節はやや数学的な話になりますが、カプラン・マイヤー推定量の数学的な背景についての話をします。カプラン・マイヤー推定量は、時点 $t_i$ における生存確率 $p_i$ を順次かけていくことによって求めますが、数学的には、時点 $t_i$ における死亡確率 $q_i$ が直接的に重要です。

生存時間が連続型確率変数である場合、死亡率は、時点 $t$ で生存していたという条件の下で、微小区間 $\Delta t$ の間に死亡する平均確率として定義されますが、生存時間が離散型変数の場合は、時点 $t_{i-1}$ に生存しているという条件の下で、次の時点 $t_i$ に死亡する確率、すなわち、 \begin{gather} h \left(t_i\right)=P \left(T=t_i\middle| t_{i-1} \le T\right)=\frac{P \left(T=t_i\right)}{S \left(t_{i-1}\right)} \end{gather} として定義されます。 そして、死亡率はハザードとも呼ばれています。

この点、カプラン・マイヤーでは、「時点 $t_i$ の直前においてリスク集合に含まれる個体の数 $n_i$」が「時点 $t_{i-1}$ に生存しているという条件」にほぼ相当し、「次の瞬間 $t_i$ に死亡する」は、時点 $t_i$ におけるイベント数 $d_i$ に対応します。すなわち、時点 $t_i$ におけるハザードは、 \begin{gather} h \left(t_i\right)=q_i=\frac{d_i}{n_i} \end{gather} となり、 時点 $t_i$ における生存確率が \begin{gather} p_i=1-h \left(t_i\right)=\frac{n_i-d_i}{n_i} \end{gather} となります。 つまり、本質的にはハザードによって生存関数を推定しているということが分かります。この点は、後のネルソン・アーレン推定量を考える際に、重要となります。

 

カプラン・マイヤー法の長所

カプラン・マイヤー法は、パラメトリックな方法と違って、生存時間の分布に特定の分布を仮定しないので、いつでもある程度の妥当性をもって実施できるという長所があります。

また、①生命保険数理法よりも観察された生存時間が正確であるため、推定の精度が高い、②集団生存曲線と生存期間中央値のような本質的な統計量を素早く算出できる、③対象者数が多数例の場合のみならず少数例の場合においても生存率を求められる、④治療方法・介入方法の違いによる予後の差（観察期間全体にわたる差）が検討できる、⑤対象者の全経過情報が生かされるなどの点も、長所とされています。

カプラン・マイヤー推定量の分散と信頼区間

グリーンウッドの公式

カプラン・マイヤー推定量は、正確には点推定量ですが、ほかの推定量と同様、標準誤差を用いて、信頼区間を算出することができます。カプラン・マイヤー推定量の標準誤差はいろいろな方法で計算できますが、次のグリーンウッド Greenwood による式$^\mathrm{(2)}$が最も有名です。 \begin{gather} V \left[\hat{S} \left(t\right)\right]= \left\{\hat{S} \left(t_j\right)\right\}^2\sum_{i=1}^{j}\frac{d_i}{n_i \left(n_i-d_i\right)}\\ \mathrm{S.E.} \left[\hat{S} \left(t\right)\right]=\sqrt{V \left[\hat{S} \left(t\right)\right]} \end{gather}

特に、観察打切り例が全くない場合は、 \begin{gather} V \left[\hat{S} \left(t\right)\right]=\frac{\hat{S} \left(t\right) \left\{1-\hat{S} \left(t\right)\right\}}{N} \end{gather} となり、 成功確率を $\hat{S} \left(t\right)$ とする二項分布の分散として表現できます。

計数過程やマルチンゲール理論により、カプラン・マイヤー推定量 $\hat{S} \left(t\right)$ とその関数が漸近的に正規分布に従うことが知られています$^\mathrm{(3),(4)}$。このため、$t_{ \left(i\right)} \le t \le t_{ \left(i+1\right)}$ における $S \left(t\right)$ の $100 \left(1-\alpha\right)\%$ の信頼区間を \begin{gather} \hat{S} \left(t\right)-Z_{0.5\alpha} \cdot \mathrm{S.E.} \left[\hat{S} \left(t\right)\right] \le S \left(t\right) \le \hat{S} \left(t\right)+Z_{0.5\alpha} \cdot \mathrm{S.E.} \left[\hat{S} \left(t\right)\right] \end{gather} と求めることができます。

一般的には、観察時間の経過にともない、リスク集合が小さくなっていくため、徐々に推定精度が下がっていき、信頼区間の幅が広くなっていきますが、打ち切りがない場合は、分母が観察開始時点のリスク集合で一定なため、推定精度は、経時的に常に悪化するというわけではありません。

補対数対数変換にもとづく分散

しかし、グリーンウッドの公式による方法は、①信頼区間の下限が0を下回る、もしくは、上限が1を上回る、ということが生じやすい、②サンプルサイズが小規模から中規模の場合には、この方法を使用する際の暗黙の前提である正規性が成り立たない、などの問題点があります。

これらの問題を解決するために、カプラン・マイヤー推定量の補対数対数変換 Complementary Log-Log transformation にもとづく方法$^\mathrm{(5)}$が用いられています。補対数対数変換にもとづくカプラン・マイヤー推定量の分散と信頼区間は、次式で与えられます。 \begin{gather} \hat{V} \left[\log{ \left\{-\log{\hat{S} \left(t\right)}\right\}}\right]= \left\{\frac{1}{\log{\hat{S} \left(t\right)}}\right\}^2 \left\{\sum_{l=1}^{j}\frac{d_l}{n_l \left(n_l-d_l\right)}\right\}\\ \end{gather} \begin{gather} \left\{\hat{S} \left(t\right)\right\}^{\exp \left(-Z_{0.5\alpha} \cdot \sigma\right)} \le S \left(t\right) \le \left\{\hat{S} \left(t\right)\right\}^{\exp \left(Z_{0.5\alpha} \cdot \sigma\right)}\\ \sigma^2=\hat{V} \left[\log{ \left\{-\log{\hat{S} \left(t\right)}\right\}}\right] \end{gather}

この方法で求めた信頼区間は、生存関数が大きいまたは小さい値のときに非対称となります。生存時間中央値 $\hat{S} \left(t\right)=0.5$ 付近でほぼ対称ですが、生存関数が1に近い値に対しては0の方向に、0に近い値に対しては1の方向に歪んでいます。ただ、この方法で求めた信頼区間は、必ず0から1の範囲に収まります。

なお、補対数対数変換のほかに、二重対数変換 $\log{ \left\{\log{\hat{S} \left(t\right)}\right\}}$、対数変換 $\log{\hat{S} \left(t\right)}$、ロジット変換 $\log{\frac{\hat{S} \left(t\right)}{1-\hat{S} \left(t\right)}}$、逆正弦平方根変換 $\sin^{-1}{\sqrt{\hat{S} \left(t\right)}}$ などの方法もあります。これらは、逆正弦平方根変換はリスク集合の大きさが少ない場合は信頼区間がほかの方法よりも広くなりますが、ほかの3つの方法は、ほぼ変わらないとされています。

 

生存時間中央値・パーセント点

定義と求め方

カプラン・マイヤー曲線を描くと、その集団の生存関数の推移を視覚的に把握することができますが、2つの集団を比較する際などには、何らかの要約指標を用いる場合があります。生存時間分析でよく用いられる指標は、生存時間中央値です。生存時間中央値は、全体のうち、生存者と死亡者の割合がちょうど50%ずつになる時点のことですが、カプラン・マイヤー曲線から生存時間中央値を推定することができます。

カプラン・マイヤー法による生存時間中央値は、 \begin{gather} {\hat{t}}_{50}=\mathrm{min} \left\{t:\hat{S} \left(t\right) \le 0.50\right\} \end{gather} と定義され、 具体的には、累積生存率が0.50の点から横軸と平行な線を引き、カプラン・マイヤー法曲線と交わった時点を読み取ります。先ほどの仮想的な生存時間データ（打ち切りがある場合）では、${\hat{t}}_{50}=6$ となります。もし、生存率曲線がある期間にわたって0.5の値のままである場合には、その最初と最後の時間の平均をとります。

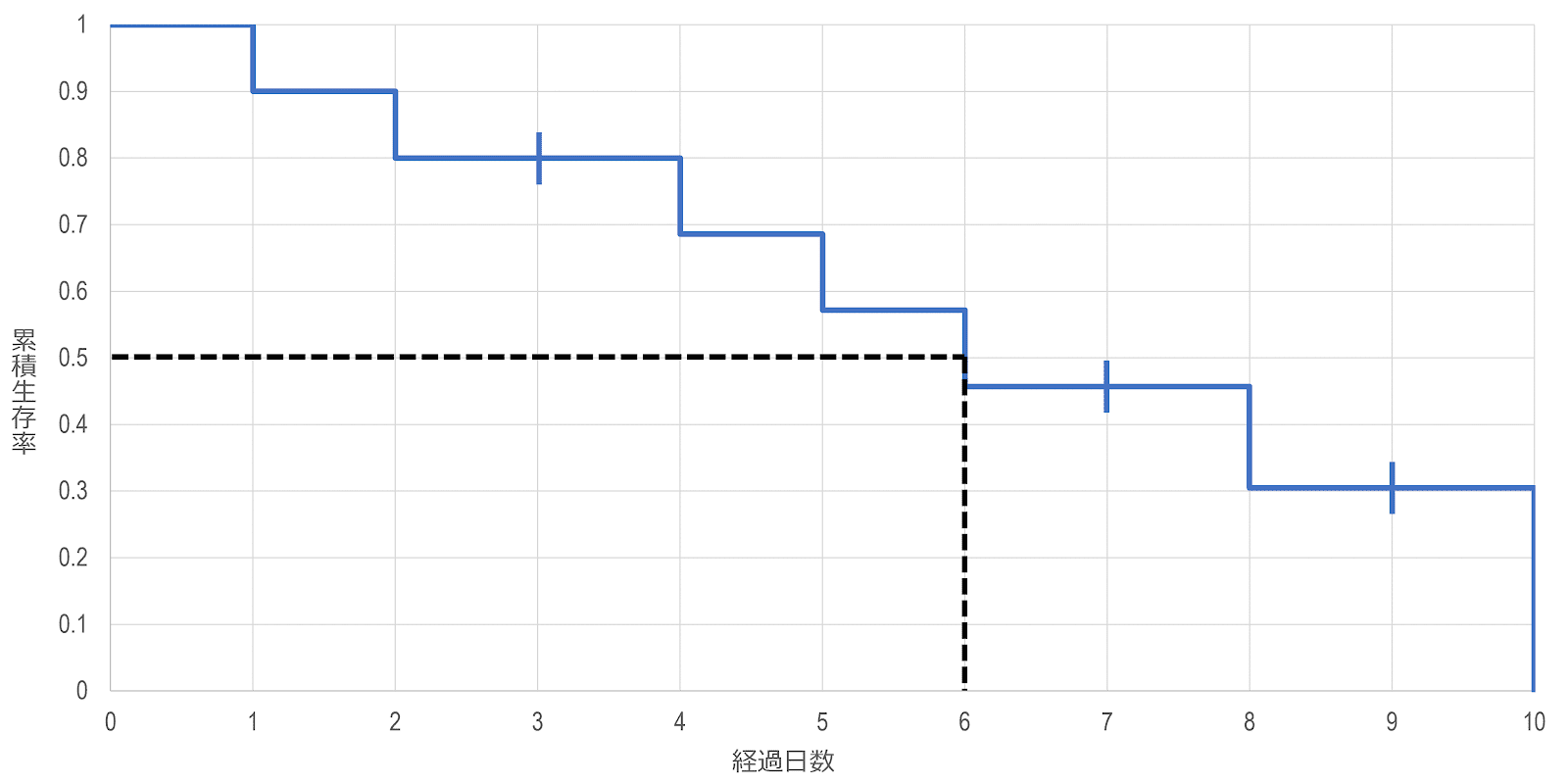
これを拡張し、一般に累積生存率が $p \left(0 \lt p \lt 1\right)$ となる点は、 \begin{gather} {\hat{t}}_p=\mathrm{min} \left\{t:\hat{S} \left(t\right) \le p\right\} \end{gather} と定義されます。

なお、カプラン・マイヤー曲線の終点が $p$ を下回らない場合、生存時間中央値やパーセント点を推定することはできません。

分散と信頼区間

パーセント点の信頼区間は、パーセント点の推定量が漸近的に正規分布に従うことを利用して求めることができます。その推定量が不偏推定量であるとの仮定の下、分散の推定量$^\mathrm{(6)}$は、 \begin{gather} V \left({\hat{t}}_p\right)=\frac{V \left[\hat{S} \left({\hat{t}}_p\right)\right]}{ \left[\hat{f} \left({\hat{t}}_p\right)\right]^2} \end{gather} と推定されます。 $V \left[\hat{S} \left({\hat{t}}_p\right)\right]$ はグリーンウッドの公式で求められた分散の推定量、$\hat{f} \left({\hat{t}}_p\right)$ は、生存時間分布の密度関数の推定量であり、 \begin{gather} \hat{f} \left({\hat{t}}_p\right)=\frac{\hat{S} \left({\hat{u}}_p\right)-\hat{S} \left({\hat{l}}_p\right)}{{\hat{l}}_p-{\hat{u}}_p} \end{gather} です。 ${\hat{l}}_p,{\hat{u}}_p$ は、${\hat{u}}_p \lt {\hat{t}}_p \lt {\hat{l}}_p$ となるように選択され、通常、 \begin{gather} {\hat{u}}_p=\mathrm{max} \left\{t:\hat{S} \left(t\right) \geq p+0.05\right\}\\ {\hat{l}}_p=\mathrm{min} \left\{t:\hat{S} \left(t\right) \le p-0.05\right\} \end{gather} とされます。 このとき、$100 \left(1-\alpha\right)\%$信頼区間の端点は、 \begin{gather} {\hat{t}}_p\pm Z_{0.5\alpha} \cdot \mathrm{S.E.} \left({\hat{t}}_p\right)\\ \mathrm{S.E.} \left({\hat{t}}_p\right)=\sqrt{V \left({\hat{t}}_p\right)} \end{gather} となります。

 

生命保険数理法

生命保険数理法は、観察期間を年あるいは月単位で区切って、区間内での死亡や打ち切りの数、区間当初の被験者数から曲線を描く（区間の幅は任意でよい）方法です。生存関数の推定法としては最も古く、古典的な方法とされており、調査・検査が一定の間隔で実施されるため、イベントの発生時点が正確には分からない（区間打ち切りがある）場合によく用いられます。例えば、何万から何十万という膨大な観察対象者を扱う行政や生命保険会社などでは、現在も生命表法が主要な方法として用いられています。

結論だけを述べると、ある区間 $i \left[t_{i-1}\right., \left.t_i\right)$ について、区間が始まったときの生存者数を $L_i$、区間 $i$ で死亡した個体数を $d_i$、打ち切りを受けた個体数を $w_i$ とするとき、ある時点 $t_i$ における累積生存率は、 \begin{gather} q_i=\frac{d_i}{n_i} \hat{S} \left(t_i\right)=\prod_{j=1}^{i} \left(1-q_j\right)\\ n_i=L_i-0.5w_i\\ L_i=L_{i-1}-d_{i-1}-w_{i-1} \end{gather} で推定されます。

生命保険数理法は、原理的にはカプラン・マイヤー法と変わらず、リスク集合の大きさの計算において、打ち切りの半数を組み込まない点が異なるだけです。このとき、$n_i$ を有効サンプルサイズ effective sample sizeと呼びます。単純に考えれば、$L_i$ で割ればよさそうですが、打ち切り例は、区間 $i$ の途中で脱落しているので、区間全体にわたってリスクに曝されていたわけではありません。そこで、生命保険数理法では、区間の半分だけリスクに曝されていたと仮定し、打ち切り例の分母に対する寄与を半分にしています。これは、打ち切りが区間で一様に起こることを想定したものです。

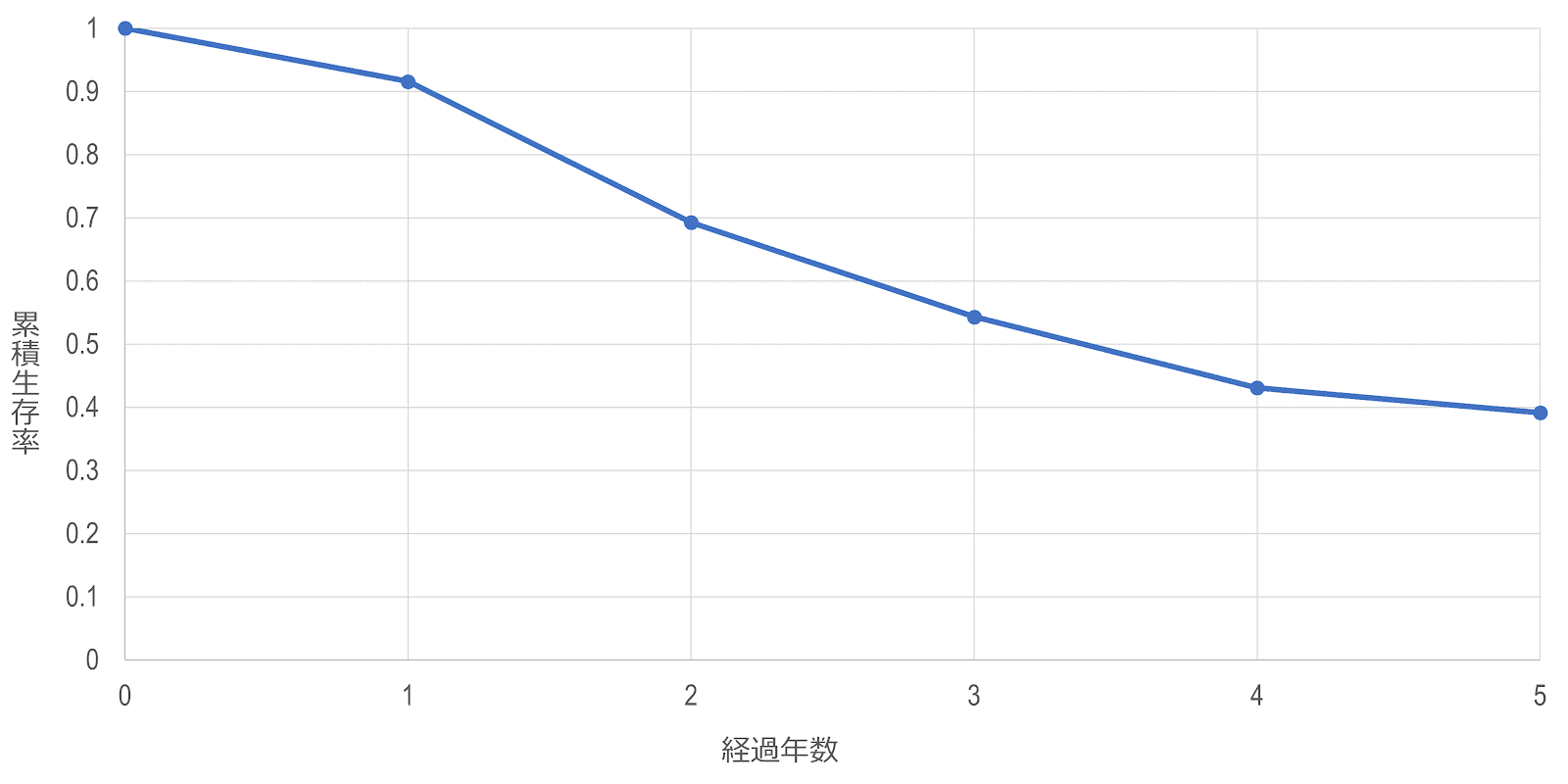
生命保険数理法の生存曲線は、カプラン・マイヤー法と異なり、各時点の累積生存率を直接つないだ折れ線型曲線になります。例えば、以下のようになります。

表5 仮想的な生存時間データ（生命保険数理法）

区間番号 $i$	区間	当初 生存数 $L_i$	打ち切り数 $w_i$	有効サンプル サイズ $n_i$	死亡数 $d_i$	死亡率 $q_i$	生存率 $p_i$	累積 生存率 $\hat{S} \left(t_i\right)$
$0$	$0$	$243$	$0$	$243$	$0$	$0$	$1$	$1$
$1$	$0-1$	$243$	$12$	$237$	$20$	$0.084$	$0.916$	$0.916$
$2$	$1-2$	$211$	$4$	$209$	$51$	$0.244$	$0.756$	$0.692$
$3$	$2-3$	$156$	$15$	$148.5$	$32$	$0.215$	$0.785$	$0.543$
$4$	$3-4$	$109$	$6$	$106$	$22$	$0.208$	$0.792$	$0.430$
$5$	$4-5$	$81$	$8$	$77$	$7$	$0.091$	$0.909$	$0.391$

 

ネルソン・アーレン推定量

ネルソン・アーレン推定量の定義

カプラン・マイヤー法は、最も頻繁に用いられる推定方法ですが、理論的に重要な他の方法にネルソン・アーレン法 Nelson-Aalen method という方法もあります。ネルソン・アーレン法$^\mathrm{(7) \sim (9)}$は、連続型の生存時間におけるハザードと累積生存率の関係 \begin{gather} S \left(t\right)=\exp \left\{-H \left(t\right)\right\}\tag{1} \end{gather} を土台として、 それを離散型生存時間に適用するというのが基本的な発想です。

離散型ハザードは、確率なので、0から1の値を取り、$T$ が取り得る値 $t_i$ 以外の時点では、離散型ハザードは0となります。離散型の累積ハザード関数は、連続型の累積の意味に対応するものとして、時間 $t$ までの各時点でのハザードの和として、 \begin{gather} \hat{H} \left(t\right)=\sum_{t_i \le t} h \left(t_i\right)=\sum_{t_i \le t}\frac{d_i}{n_i} \end{gather} と定義され、 この推定量は、累積ハザード関数のネルソン・アーレン推定量と呼ばれています。
このとき、時点 $t$ における累積生存率のネルソン・アーレン推定量は、 \begin{gather} \hat{S} \left(t\right)=\exp \left\{-\hat{H} \left(t\right)\right\} \end{gather} で与えられます。

累積ハザード関数 $H \left(t\right)$ を離散型変数として上記のように定義する場合、式 $(1)$ の関係は厳密には成り立ちませんが、区分指数モデルという仮定や計数過程の理論を用いることで、離散型変数の場合に拡張しています。区分指数モデル piecewise exponential model とは、ハザード関数が連続したイベント時点と時点の間で、区分的に定数であるとする仮定、すなわち、区間 $t\in \left(t_{i-1}\right., \left.t_i\right]$ において、 \begin{gather} h \left(t\right)=h \left(t_i\right) \end{gather} とする仮定です。

カプラン・マイヤー推定量とネルソン・アーレン推定量の関係

カプラン・マイヤー推定量とネルソン・アーレン推定量は、それぞれ \begin{gather} {\hat{S}}_{\mathrm{KM}} \left(t\right)=\prod_{i=1}^{j} \left(1-\frac{d_i}{n_i}\right)\\ {\hat{S}}_{\mathrm{NA}} \left(t\right)=\prod_{i=1}^{j}\exp \left(-\frac{d_i}{n_i}\right) \end{gather} で与えられます。 ここで、テイラー展開を用いると、一般に、$0 \lt x \lt 1$ を満たす任意の $x$ に対して、 \begin{gather} 1-x \le e^{-x} \end{gather} が成り立つので、 $x=\frac{d_i}{n_i}$ として、 \begin{align} {\hat{S}}_{\mathrm{KM}} \left(t\right) \le {\hat{S}}_{\mathrm{NA}} \left(t\right) \end{align} すなわち、ネルソン・アーレン推定値は、常にカプラン・マイヤー推定値以上の値を取ります。

ここで、$h \left(t_i\right)\rightarrow0$ のとき、 \begin{gather} 1-h \left(t_i\right)\cong\exp \left\{-h \left(t_i\right)\right\}\\ \Leftrightarrow\prod_{t_i \le t} \left\{1-h \left(t_i\right)\right\}\cong\exp \left\{-\sum_{t_i \le t} h \left(t_i\right)\right\} \end{gather} が成り立つため、 \begin{gather} S \left(t\right)\cong\prod_{t_i \le t} \left\{1-h \left(t_i\right)\right\} \end{gather} となります。 これは、カプラン・マイヤー推定量とネルソン・アーレン推定量が漸近的にほぼ同じ値になることを示しています。

 

参考文献

• 大橋 靖雄, 浜田 知久馬 著. 生存時間解析：SASによる生物統計. 東京大学出版会, 1995, p.1-21
• 前谷 俊三 著. 臨床生存分析：生存データと予後因子の解析. 南江堂, 1996, p.11-25
• ダグラス・アルトマン 著, 木船 義久, 佐久間 昭 訳. 医学研究における実用統計学. サイエンティスト社, 1999, p.297-300, p.304-306
• 中村 剛 著. Cox比例ハザードモデル. 朝倉書店, 2001, p.11-16
• 浜田 知久馬 著. 学会・論文発表のための統計学：統計パッケージを誤用しないために. 真興交易医書出版部, 2012, p.218-222
• デビッド・ホスマー, スタンリー・レメショウ, スーザン・メイ 著, 五所 正彦 監訳. 生存時間解析入門. 東京大学出版会, 2014, p.17-47
• 西川 正子 著. カプラン・マイヤー法：生存時間解析の基本手法. 共立出版, 2019, p.14-53
• ジョン・ラチン 著, 宮岡 悦良 監訳, 遠藤 輝, 黒沢 健, 下川 朝有, 寒水 孝司 訳. 医薬データのための統計解析. 共立出版, 2020, p.464-469
• Clark, T.G., Bradburn, M.J., Love, S.B. et al.. Survival analysis part I: basic concepts and first analyses. Br J Cancer. 2003, 89(2), p.232-238, doi: 10.1038/sj.bjc.6601118
• 藤田 烈. 疫学・統計解析シリーズ：生存時間解析結果を読み解くための基礎知識. 日本環境感染学会誌. 2014, 29(5), p.313-323, doi: 10.4058/jsei.29.313

引用文献

1. Kaplan, E.L. & Meier, P.. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association. 1958, 53(282), p.457-481, doi: 10.1080/01621459.1958.10501452
2. Greenwood, M.. The errors of sampling of the survivorship tables. Reports on Public Health and Medical Subjects. 1926, 33(Appendix 1), p.1-26.
3. Fleming, T.R. & Harrington, D.P.. Counting Processes and Survival Analysis. Wiley & Sons, Inc., 2005, 454p.
4. Andersen, P.K., Borgan, Ørnulf, Gill, R.D. et al.. Statistical Models Based on Counting Processes. Springer Verlag, 1993, 784p.
5. Kalbfleisch, J.D. & Prentice, R.L.. The Statistical Analysis of Failure Time Data. 2nd Edition, John Wiley & Sons, Inc., 2002, 462p.
6. デービット・コレット 著, 宮岡 悦良 監訳. 医薬統計のための生存時間データ解析. 共立出版, 2013, 422p.
7. Aalen, O.. Nonparametric Inference for a Family of Counting Processes. The Annals of Statistics. 1978, 6(4), p.701-726, doi: 10.1214/aos/1176344247
8. Nelson, W.. Hazard Plotting for Incomplete Failure Data. Journal of Quality Technology. 1969, 1(1), p.27-52, doi: 10.1080/00224065.1969.11980344
9. Nelson, W.. Theory and Applications of Hazard Plotting for Censored Failure Data. Technometrics. 1972, 14(4), p.945-966, doi: 10.1080/00401706.1972.10488991

関連記事

• 観察の打ち切りと生存関数
• 生存曲線の比較
• 比例ハザードモデル
• コホート研究【生存時間】
• カプラン・マイヤー法
• 生存時間分布のパラメトリックモデル①：指数分布モデル
• 生存時間分布のパラメトリックモデル②：ワイブル分布モデル
• 生存時間分布のパラメトリックモデル③：加速死亡時間モデル
• 生存時間分布のパラメトリックモデル④：対数ロジスティック分布モデル
• 生存時間分布のパラメトリックモデル④：対数ロジスティック分布モデル