医学の分野では、さまざまな疾病の予防や予後予測を行うために、診断検査が行われることがありますが、その有用性は、実施コストや精度、正確性など、さまざまな観点から評価されます。本稿では、診断検査の正確性にまつわる、感度・特異度、陽性・陰性的中度、陽性・陰性尤度比、カットオフ値とROC曲線などの概要を解説しています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
診断と検査
疾病への対処の基本は、まず第1に1次予防 primary prevention、つまり、生活習慣の改善、生活環境の改善、健康教育による健康増進を図り、予防接種による疾病の発生予防、事故防止による傷害の発生を予防することです。
ただ、すべての疾患を予防することができるわけではないので、次善の策として2次予防 secondary preventionである発生した疾病や障害を検診などにより早期に発見し、早期に治療や保健指導などの対策を行ない、疾病や傷害の重症化を予防するという対応が必要となります。
それでも防ぎきれなかった疾病については、3次予防 tertiary prevention で対処します。つまり、治療の過程において保健指導やリハビリテーション等による機能回復を図るなど、社会復帰を支援し、再発を予防することです。
こうしたことには、医師をはじめとしたさまざまな専門家の協力が必要となりますが、多くの場合、患者は専門家の判断にもとづいて、予防や治療を行います。この判断のうち、最も初期に下される判断が「診断」です。診断 diagnosis とは、診察や検査を通じて、医者が患者の健康状態、病気の種類や病状などを判断すること
を指し、単純に言えば、例えば「あなたは風邪の状態にあります」とか「あなたの胃にはごく初期のがんがあります」ということを事実として認定するということです。
患者の医学的な状態を的確に診断することは適切な治療の開始に影響し、患者の予後へとかかわっていくためとても重要です。ただ、診断(判断)を下すためには、その結論を導くための「根拠」や「証拠」が必要となります。そうした「証拠」となる情報を集めるために、診察(問診・視診・触診・打診・聴診など)や検査が行われます。
現在ほど医療が発達していない時代では、医師の「経験」や「勘」などが主な診断の根拠となっていましたが、現在は、生化学的検査、生理機能検査、画像解析、遺伝子検査など、より客観的で科学的な手法が数多く確立されています。このように、診断を行うための判断材料を集めることを目的としている検査を診断検査 diagnostic test と呼びます。
予後予測とスクリーニング
診断検査は、「病気があるかないか」の診断以外にも、①患者の予後予測や②スクリーニングなどの目的にも用いることができます。
①患者の予後予測とは、例えば、「55歳男性、高血圧、運動不足、塩分摂取量が多い食生活」などの予測因子を持った人が「将来、心筋梗塞を発症するか?」といった問題に対し、その発症確率などを予測するということで、アメリカのフラミンガム研究において開発されたリスクスコアという指標やロジスティック回帰などの手法が有名です。
スクリーニング screening とは、迅速に実施可能な試験、検査、その他の手技を用いて、 無自覚の疾病異常または欠陥を暫定的に識別すること
を指します。より分かりやすくいうと、ある疾病に関する自覚症状がなく、一見、健康そうに見える人々の中から、実際には疾病に罹患していると思われる人々を、疾病に罹患していないと思われる人々から区別して選び出すことです。COVID-19に対するPCR検査などが典型的な例で、スクリーニングにより「早期発見・早期治療」を実現し、感染者の拡大や重症化リスクの増大を予防します。
先にも述べたように、疾病への対処の基本は1次予防です。この点、予後予測やスクリーニングは1次予防に役立つものであるため、さまざまな検査法や診断法を開発することには相応の意義があり、それらの開発や評価を目的とした研究も数多く実施されています。
スクリーニングと確定診断
スクリーニングは、あくまでもその疾病に罹患している可能性が高い人を選別するためのものであり、スクリーニングの結果によって、最終診断や確定診断が下されるわけではありません。スクリーニング検査で異常(または異常を疑わせる)所見が見られた場合、さらに精密検査を実施し、疾病の有無とその程度の判定をすることになります。
診断のゴールド・スタンダードがある場合、確定診断はゴールド・スタンダードにもとづいて下されます。ゴールド・スタンダード gold standard とは、がんの生検検体の病理検査などのように、ある疾患の有無を示す標準的指標として一般的に認められているものを指します。疾患によっては、定義上のゴールド・スタンダード definitional gold standard が存在するものもあります。たとえば、冠動脈造影で少なくとも1つの主幹動脈に50%以上の狭窄がある場合を、冠動脈疾患と定義するといった基準がそうです。また、リウマチ性疾患などのように、罹患の基準として「徴候、症状、臨床検査異常の中で、最低いくつかを満たす場合」といった症候群的定義が用いられる疾患や時には、神経変性疾患のように剖検によってのみ正確な診断が可能な場合もあります。
後述するように、完全な正確性をもつ検査は存在せず、疾病のある人とない人を完璧に識別できることは滅多にありません。ゴールド・スタンダードがない場合、多くの状況で、診察や検査から得られたさまざまな情報や専門家どうしの議論などにもとづいて、最終診断が下されることになります。
診断検査の意義と有用性
診断検査を行うことは、疾病の1次予防を考えるうえで重要なことではありますが、必ずしもすべての疾病に対して有効・有用であるわけではありません。その疾病に関する診断検査の意義は、①疾病の重篤度、②早期発見が予後の改善につながること、③症状出現以前における、集団全体の疾病の有病率がある程度高いこと、④実施可能性(コストや実施の難易度)、などの観点から評価されます。
①の重篤度は、効率性や倫理性といった観点から必要となります。診断検査を実施するためには、実施者・患者双方の時間や労力、費用などがかかり、患者にとっては、検査すること自体に起因するリスクもあります。このリスクには、例えば、診断検査での判断が間違っていた場合の負担などがあります。先述したように、診断検査は百発百中というわけにはいかず、一定の割合で間違った判定をすることがあります。このとき、例えば「あなたの胃にはがんがあるようです」という診断が下されたとします。このとき、たいていの人は「死に至る病」の代表格である「がん」であることに大変なショックを受けるでしょう。しかし、これが間違いだった場合、「間違いであってよかった」とほっとするいっぽうで、受けたショックとストレスによって縮んだ寿命は取り消すことはできません。また、既に何らかの治療を開始してしまった後に間違いであったことが判明すると、既に治療に伴う副作用を身体的・精神的に受けているかもしれませんし、治療のための費用も無駄になってしまいます。こうした面があるため、病気が重篤でなかったり、重篤な状態やQOLの悪化を招いたりしない場合、診断検査の有用性は低くなります。
また、診断検査によって疾病を早期発見できたとしても、それが臨床的な価値に直結しない場合もあります。有用な治療法がなかったり、高額な治療法であったり、非常に限られた施設でしかできない治療法であったりすると、診断された人びとが容易に治療を受けられません。得られた検査結果にもとづいて、患者の利益につながる効果的な対応が行われてはじめて、検査実施の価値が得られます。また、早期治療する方が、遅れて治療する(スクリーニングを実施せずその疾患が発見されてから治療を開始する)よりも有益でなければ、検査の意義を見出すことが難しくなります。
くわえて、後述するように、診断検査での判断が間違っている確率は、その疾病のもともとの有病率に大きく左右され、有病率が低い集団を対象にスクリーニングを実施すると、空振り(偽陽性)が多くなり、精密検査についての負担が増加してしまいます。
最後に、検査法そのものが侵襲的であったり、高額であったり、検査ができる施設が少なかったりすると検査法は普及しにくいでしょう。身体的、経済的な負担が少なく、どこでも簡単にできることが求められるということです。
以上のような点を考えた場合、たとえば高血圧のスクリーニングは、(1)高血圧が危険因子である脳血管疾患や虚血性心疾患などは生命やADL/QOL について極めて重大な結果をもたらす、(2)血圧の適切なコントロールによってこれらの重大な結果のリスクを低下させることができる、(3)有病率が高い、という3 点の要件を満たしており、スクリーニングの対象として適切です。
診断検査の性能評価
前節で述べたような観点で評価を行い、その検査を行うこと自体に意義があるのであれば、次は診断検査の性能について評価する必要があります。そうした診断検査の性能は、主に①精度(再現性・信頼性)や②正確性・妥当性などの観点から評価されます。
精度とは、単純に言うと、測定の安定性や測定結果のばらつきを表す概念で、誰が、いつ、どこで測定したとしても同じような結果になる場合、「精度が高い」と表現されます。
例えば、ある人のストレス状態を面接調査で評価する際に「最近、ちょっと忙しくて、趣味の時間が取れなくて」という発言があったとき、ある人は「まあ、そこまで大きな影響はないかな?」と判断し、また別の人は「趣味の時間が取れないということは、今、ストレスをためこんじゃっているのかな?」と判断するかもしれません。
また、例えば、コルチゾールなどのストレスホルモンは、分泌量に日内変動があることが知られており、測る時間によって、測定値にばらつきが生じることがあります。さらに、ある研究機関では最先端の高性能機器を使って分析するいっぽう、別の期間は何世代か前の型落ちした機器で分析するということもあります。
このように、測定は人や条件などによって結果にばらつきが生じ得ますが、できる限り、そのばらつきが小さい検査方法が良いということです。
これに対し、正確性とは、その診断検査の正しさの程度を意味するもので、ざっくりと言えば、本当にその疾病に罹患している人としていない人をどの程度正確に判別できるかの能力といいかえることができます。この点については、後で詳しく説明していきます。
これまでに述べてきたように、診断検査を評価する際には、さまざまな観点があり、それらを総合的に判断する必要があります。しかし、現実的にはほとんどの場合、診断検査をアウトカム改善の観点から評価することは難しく、一般には、正確性、安全性、コストなどを既存の検査と比較することによって評価されます。したがって、新しい診断検査を開発するときには、精度、正確性、価格、安全性、実施の難しさなど、既存の方法のどこを最も改善すべきなのかを十分に検討することが大切です。
診断検査の正確性
診断検査の正確性とは、疾病の有無を判別する能力のことですが、先にも述べたように、ほとんどの場合、真の状態(罹患の有無)と検査結果は完全には一致しないため、問題は検査結果がどれくらいの確率で正しいのかということになります。診断検査の結果は陽性・陰性の二値で表される場合と、1+、2+、3+のような順序変数、CRP(C反応性タンパク)のような連続変数の場合があり、検査の正確性を評価する指標には、感度・特異度、陽性的中度・陰性的中度、尤度比などがあります。以下で、それぞれの指標について詳しく見ていきます。
なお、それぞれの用語を説明するにあたり、話を単純にするために、診断検査による判定は「ある状態にあるか否かの二値データ」にもとづいて行うとします。診断検査では、関心のあるアウトカムが発生している(疾病あり)と判定することを陽性 positive、関心のあるアウトカムが発生していない(疾病なし)と判定することを陰性 negative と表現します。
例えば、「ある人がインフルエンザかどうか」を「発熱や身体のだるさなどの自覚症状があるか否か」によって判定し、検体検査の結果にもとづいて確定診断を下すといった場合です。このとき、検査結果と疾病の保有状況が以下の表のようにまとめられるとします(この場合、例えば、「自覚症状あり」が「陽性」、「自覚症状なし」が「陰性」ということになります)。
| 陽性 $ \left(+\right)$ | 陰性 $(-)$ | 合計 | |
|---|---|---|---|
| 疾病あり $ \left(D\right)$ | $a$ | $c$ | $n_1$ |
| 疾病なし $(\bar{D})$ | $b$ | $d$ | $n_0$ |
| 合計 | $m_1$ | $m_0$ | $N$ |
感度と特異度
指標の定義
診断検査を評価する際にまず考えられるのは、「当たり」が多い検査、すなわち「罹患している者は陽性、罹患していない人は陰性」という結果が出る確率が高い検査であるかどうかです。これを正診率 accuracy といい$^\mathrm{(i)}$、 \begin{gather} \mathrm{\hat{A}}=\frac{a+d}{N} \end{gather} で定義されます。
しかし、一般的には、この正診率で検査の評価が行われることはありません。なぜなら、有病率のあまり高くない疾患に対する検査で、実際に検査を行わずにすべての検体を「陰性」と報告しても、正診率は高くなるからです$^\mathrm{(ii)}$。
したがって、全体としての正答率ではなく、真に疾患に罹患しているかどうかで二分して、検証します。この分割したときの代表的な指標が感度と特異度です。
感度 sensitivity、あるいは、真陽性率 ture positive rate は、以下のように有病者の中で検査結果が正しく陽性となる者の割合として定義され、真に疾患のある人において、検査により疾患であることを特定できる確率(割合)を表しています。 \begin{gather} \mathrm{\widehat{Sen}}=P \left(+\middle| D\right)=\frac{a}{n_1} \end{gather}
特異度 specifivity、あるいは、真陰性率 ture negative rate、以下のように無病者の中で検査結果が正しく陰性となる者の割合として定義され、真に疾患のない人において検査により疾患がないことを特定できる確率(割合)を表しています。 \begin{gather} \mathrm{\widehat{Spe}}=P \left(-\middle|\bar{D}\right)=\frac{d}{n_0} \end{gather}
また、無病者の中で検査結果が誤って陽性になる者の割合を偽陽性率 false positive rate と呼び、以下で定義されます。 \begin{gather} \mathrm{\widehat{FP}}=P \left(+\middle|\bar{D}\right)=\frac{b}{n_0} \end{gather}
また、有病者の中で検査結果が誤って陰性になる者の割合を偽陰性率 false negative rate と呼び、以下で定義されます。 \begin{gather} \mathrm{\widehat{FN}}=P \left(-\middle| D\right)=\frac{c}{n_1} \end{gather}
指標同士の関係
検査の感度が高ければ、疾患をもつ人を間違って陰性(偽陰性)と判定する頻度が低くなります。そのため、感度と偽陰性率との間には \begin{gather} \mathrm{\widehat{Sen}}=1-\mathrm{\widehat{FN}} \end{gather} の関係が成り立ちます。
また同様に、特異度が高ければ、疾患をもたない人を間違って陽性(偽陽性)と判定する頻度は低くなるため、特異度と偽陽性との間には \begin{gather} \mathrm{\widehat{Spe}}=1-\mathrm{\widehat{FP}} \end{gather} の関係が成り立ちます。
指標の算出状況と意味
診断検査の感度と特異度は、疾患(またはある状態)をもつことがわかっている群と疾患をもたないことがわかっている別の群とを選び、双方に検査を実施することで算出できます。つまり、これらの指標は、先に確定診断した後、「答え」が分かっている状況で検査を実施し、発症群と非発症群でどれくらい正解できるかを調べるときに用いる指標であり、診断法の開発段階で、その診断法がきちんと発症者と非発症者を識別する能力があるかを確認する際に用いるものです。
感度、特異度、偽陽性率、偽陰性率は、本質的に「割合」であるため、すべて0~1の間の値をとり、感度・特異度が1に近いほど(偽陽性率・偽陰性率が0に近いほど)診断の力が強いことを表します。
陽性的中度と陰性的中度
ただ、実際の診断は、診断検査の結果にもとづいて、その人が発症者なのかを判断するという方向であり、問題となるのは、陽性・陰性の結果がどれくらい信頼できる(正しい)のかという点です。これらを評価するのが陽性的中度と陰性的中度です。
陽性的中度 positive predictive value: PPV、陽性予測値とは、検査が陽性だった人の中で、実際に疾患のある人の割合のことを指し、以下で定義されます。 \begin{gather} \mathrm{\widehat{PPV}}=P \left(D\middle|+\right)=\frac{a}{m_1} \end{gather}
陰性的中度 negative predictive value: NPV、陰性予測値とは、検査が陰性だった人の中で、実際に疾患のない人の割合のことを指し、以下で定義されます。 \begin{gather} \mathrm{\widehat{NPV}}=P \left(\bar{D}\middle|-\right)=\frac{d}{m_0} \end{gather}
陽性的中度と陰性的中度は、検査の実用段階において、用いられる指標です。このうち、陽性の結果が出た人の中には、一定の割合で偽陽性(実際は疾病をもたない)の人が含まれるため、陽性者をさらに精密検査することで確定診断を下すことになります。
偽陽性のパラドックス:「有病率」がもたらす罠
診断法を開発している際、感度と特異度が高くなっていることが確認できれば、おそらく陽性・陰性的中度も高いはずであり、「良い診断法が開発できた」と安堵するかもしれません。しかし実は、とても注意しなければならない罠が潜んでいるのです。
例えば、全体における有病率 $\mathrm{P}$ が0.1% と非常に珍しい病気の診断検査法を開発し、感度が90%、特異度が99% であることが確認されたとしましょう。そこで、この検査を10000人に実施したところ、次のような結果になりました。
| 陽性 $ \left(+\right)$ | 陰性 $(-)$ | 合計 | |
|---|---|---|---|
| 疾病あり $ \left(D\right)$ | $9$ | $1$ | $10$ |
| 疾病なし $(\bar{D})$ | $100$ | $9890$ | $9990$ |
| 合計 | $109$ | $9891$ | $10000$ |
この結果から、感度と特異度を求めると、 \begin{gather} \mathrm{\widehat{Sen}}=\frac{9}{10}=90\%\\ \mathrm{\widehat{Spe}}=\frac{9890}{9990}\cong99\% \end{gather} となり、 検証段階で確認した通りの性能を発揮していることが示されました。
しかし、同様に陽性的中度・陰性的中度を計算してみると、 \begin{gather} \mathrm{\widehat{PPV}}=\frac{9}{109}\cong8\%\\ \mathrm{\widehat{NPV}}=\frac{9890}{9891}\cong99.9\% \end{gather} となります。 陰性的中度は99.9%とこの上ない性能を発揮していますが、陽性的中度の方はなんとたったの8%しかなく、検査結果がほとんど信用できない結果となってしまいました。これは、もともとの有病率が非常に小さかったため、偽陽性の数が真陽性の数を大幅に上回ってしまったことが原因で発生してしまった現象です。
このような現象は、偽陽性のパラドクス false positive paradox として知られる、非常に有名な現象です。このように、陽性的中度は、感度だけでなく、有病率にも大きな影響を受けてしまいます。この例では、陰性的中度はほぼ100%であることから、陰性の結果が出れば、ほぼ確実にその人は「発症者ではない」と断言できます。そのいっぽう、陽性となった人の結果はほとんどあてにはならないため、そうした意味においても、スクリーニング検査によって候補者を絞り込み、精密検査を行うことで確定診断を下す必要があります。
陽性尤度比と陰性尤度比
指標の定義
ただ、この例をもう少し冷静に見てみると、また別の見方をすることもできます。検査をする前の段階で、受検者全員に「あなたは発症者です」と言った場合、それが当たっている確率は、全体の有病率と同じ0.1%です。
それが検査を行った結果、陽性者全員に対して「あなたは発症者です」と言った場合、当たる確率は低く、実用的ではないものの、約8%にまで上昇しています。そういう意味で、検査を行ったことには、ある程度の意味があったと評価することもできます。
この話の中で、ある人が検査を行う前に疾病を有している確率を疾病の事前確率 prior probability と呼び、検査を行った後、ある人が疾病を有している確率を疾病の事後確率 posterior probability と呼びます。検査の性能をこれら事前確率と事後確率の観点から評価する指標に、陽性尤度比と陰性尤度比があります。
陽性尤度比 positive likelihood ratio は、偽陽性率に対する真陽性率の比として、 \begin{gather} \mathrm{\widehat{PLR}}=\frac{\mathrm{\widehat{Sen}}}{\mathrm{\widehat{FP}}}=\frac{\mathrm{\widehat{Sen}}}{1-\mathrm{\widehat{Spe}}}=\frac{an_0}{bn_1} \end{gather} で定義されます。 表2の例では、 \begin{gather} \mathrm{\widehat{PLR}}=\frac{0.9}{0.01}=90 \end{gather} となります。 これは、有病者が無病者よりも何倍陽性になりやすいかを表す指標になっています。陽性尤度比が1のとき、有病者と無病者で「陽性のなりやすさ」が変わらないということなので、検査としては意味がありません。この値は高ければ高いほど良く、10より大きくなると「有効な検査」であるとされています。
陰性尤度比 negative likelihood ratio は、真陰性率に対する偽陰性率の比として、\begin{gather} \mathrm{\widehat{NLR}}=\frac{\mathrm{\widehat{FN}}}{\mathrm{\widehat{Spe}}}=\frac{1-\mathrm{\widehat{Sen}}}{\mathrm{\widehat{Spe}}}=\frac{cn_0}{dn_1} \end{gather} で定義されます。 表2の例では、 \begin{gather} \mathrm{\widehat{NLR}}=\frac{0.1}{0.99}\cong0.1 \end{gather} となります。 これは有病者が無病者よりも何倍陰性になりやすいかを表す指標になっています。陰性尤度比が1のとき、罹患者と非罹患者で「陰性のなりやすさ」が変わらないということなので、検査としては意味がありません。この値は低ければ良く、0.1よりも小さくなると「有効な検査」であるとされています。
陽性尤度比と陰性尤度比の利用法
検査の有用性を尤度比で評価して調べる場合には、有病率そのものの代わりに有病オッズを使います。
例えば、ある疾患の有病率が $\mathrm{P}$ だとします。検査前ではある人が有病である確率は有病率 $\mathrm{P}$ に一致します。つまり、ある人の有病状況に関する検査前確率は、 \begin{gather} \mathrm{P}=\frac{n_1}{N} \end{gather} 検査前オッズ pre-test odds は、 \begin{gather} \frac{\mathrm{P}}{1-\mathrm{P}}=\frac{\frac{n_1}{N}}{1-\frac{n_1}{N}}=\frac{\frac{n_1}{N}}{\frac{n_0}{N}}=\frac{n_1}{n_0} \end{gather} となります。
いっぽう、検査後においては、ある人が有病である確率は陽性的中度 $\mathrm{PPV}$ に一致します。つまり、ある人の有病状況に関する検査後確率は、 \begin{gather} \mathrm{\widehat{PPV}}=\frac{a}{m_1} \end{gather} 検査後オッズ post-test odds は、 \begin{gather} \frac{\mathrm{\widehat{PPV}}}{1-\mathrm{\widehat{PPV}}}=\frac{\frac{a}{m_1}}{1-\frac{a}{m_1}}=\frac{\frac{a}{m_1}}{\frac{b}{m_1}}=\frac{a}{b} \end{gather} となります。
これらと陽性尤度比の定義式を見比べてみると、 \begin{gather} \mathrm{\widehat{PLR}}=\frac{\mathrm{\widehat{PPV}}}{1-\mathrm{\widehat{PPV}}}\times\frac{1-\mathrm{P}}{\mathrm{P}}\\ \frac{\mathrm{\widehat{PPV}}}{1-\mathrm{\widehat{PPV}}}=\mathrm{\widehat{PLR}}\times\frac{\mathrm{P}}{1-\mathrm{P}} \end{gather} つまり、 検査後オッズ=陽性尤度比×検査前オッズ という関係が成り立つことが分かります。
このことは、検査を行ったことによって、検査前オッズが陽性尤度比の分だけ倍増(上昇)し、陽性と判定されたという情報によって、その人が有病者であることの確からしさ(≒オッズ)が上がったと解釈することが可能で、こうした観点から、検査を行うことの有用性を評価することもできるということになります。
カットオフ値:感度と特異度の関係
先にも述べたように、診断検査の結果は、陽性・陰性の二値で表される場合だけでなく、順序変数や連続変数で示される場合もあります。しかし、そのような場合でも、ある値を境にして陽性と陰性に分けることで、これまでの議論をそのまま適用できるようになります。このような閾値のことをカットオフ値 cutoff value といいます。例えば、その検査値が低い値が正常で、高い値が以上である場合、あるカットオフ値 $\mathrm{C}$ より高い値は陽性と判断され、低い値は陰性として判断されます。連続値の検査値が正規分布に従うとすると、以下のようなイメージとなり、一定の偽陽性と偽陰性が発生します。
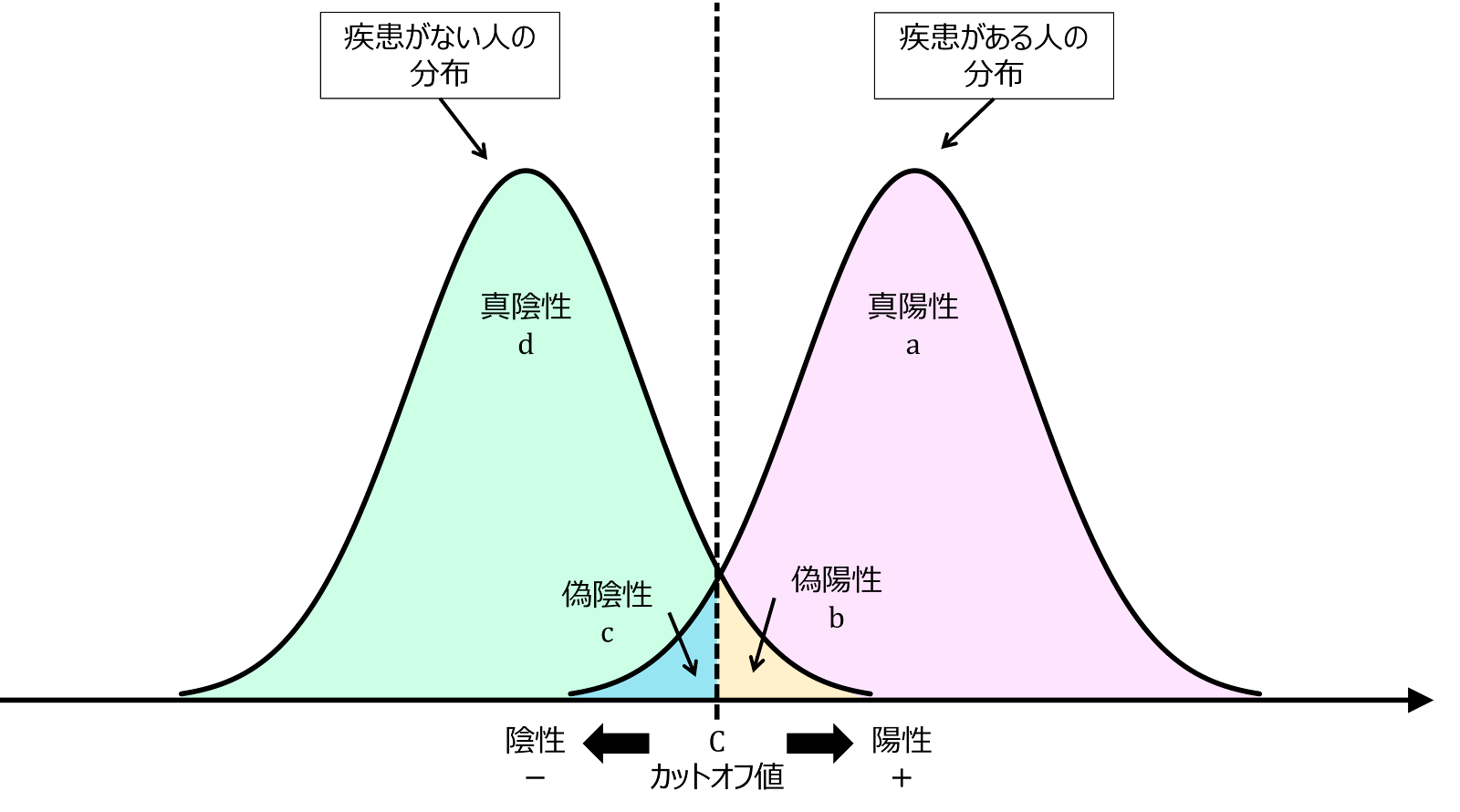
カットオフ値は、研究者が任意に決めることができますが、カットオフ値を小さい値に設定、つまり基準を甘くすると、陽性が多くなり、感度が上がるかわりに偽陽性も増え、特異度が低下します。逆に基準をきつくすれば、感度が下がる代わりに特異度は上がります。これは、統計的仮説検定における棄却閾値、有意水準、検出力の関係と似た関係で、感度と特異度の間にはトレード・オフの関係があります。
ROC曲線
ただ実質的には、カットオフ値を決めると感度と特異度は自動的に決まるため、2つを別個のものとして考える必要はなく、セットとして考えた方が扱いやすくなります。この関係を分かりやすく表現する方法としてROC曲線があります。
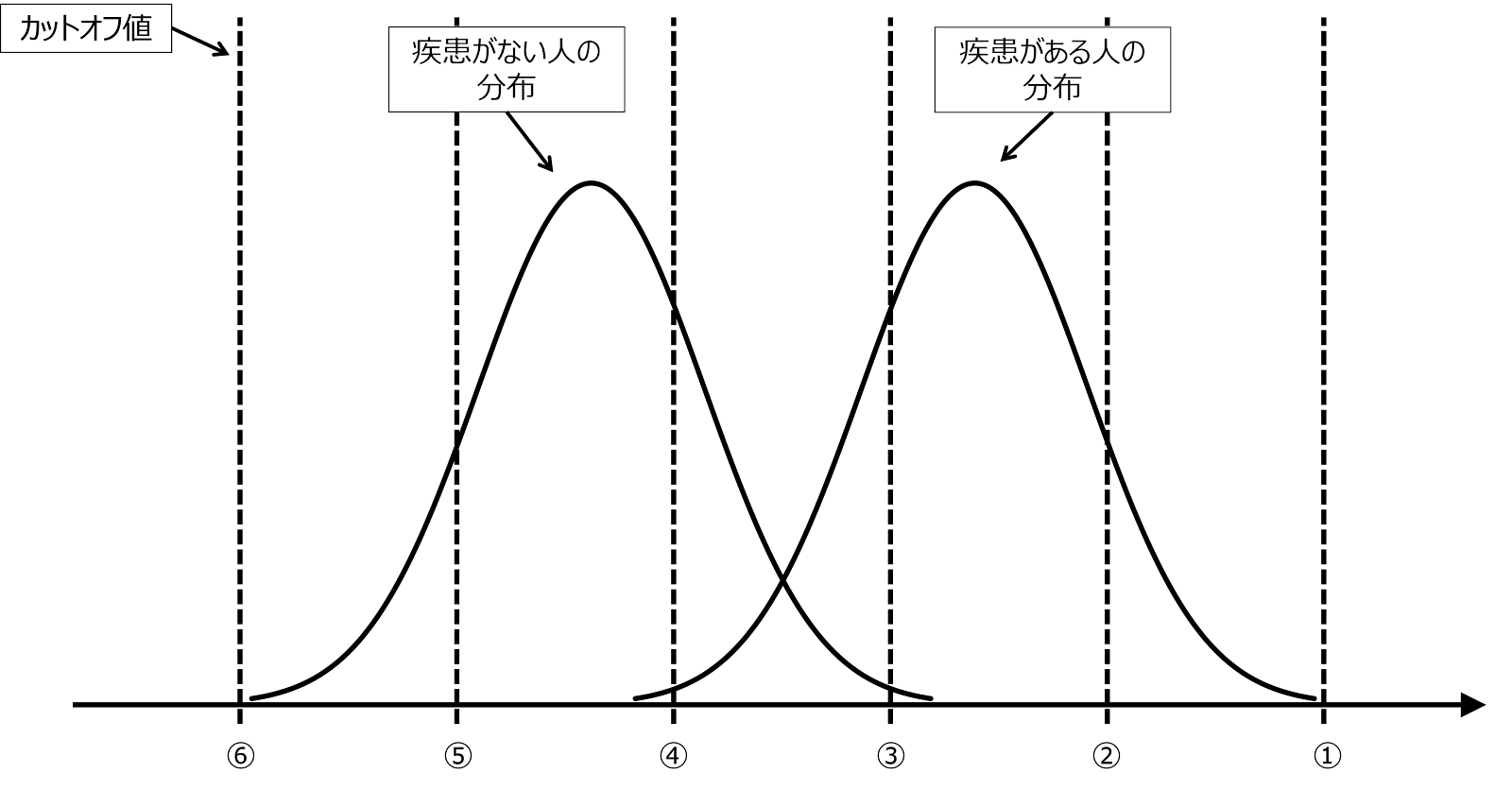
ROC曲線 receiver operating characteristic curve$^\mathrm{(iii)}$ とは、カットオフ値を動かし、そのときの感度(真陽性率)を縦軸に、1-特異度(偽陽性率)を横軸にプロットしたものです。例えば、先ほどの図のようにカットオフ値を変化させていった場合、以下のようになります。
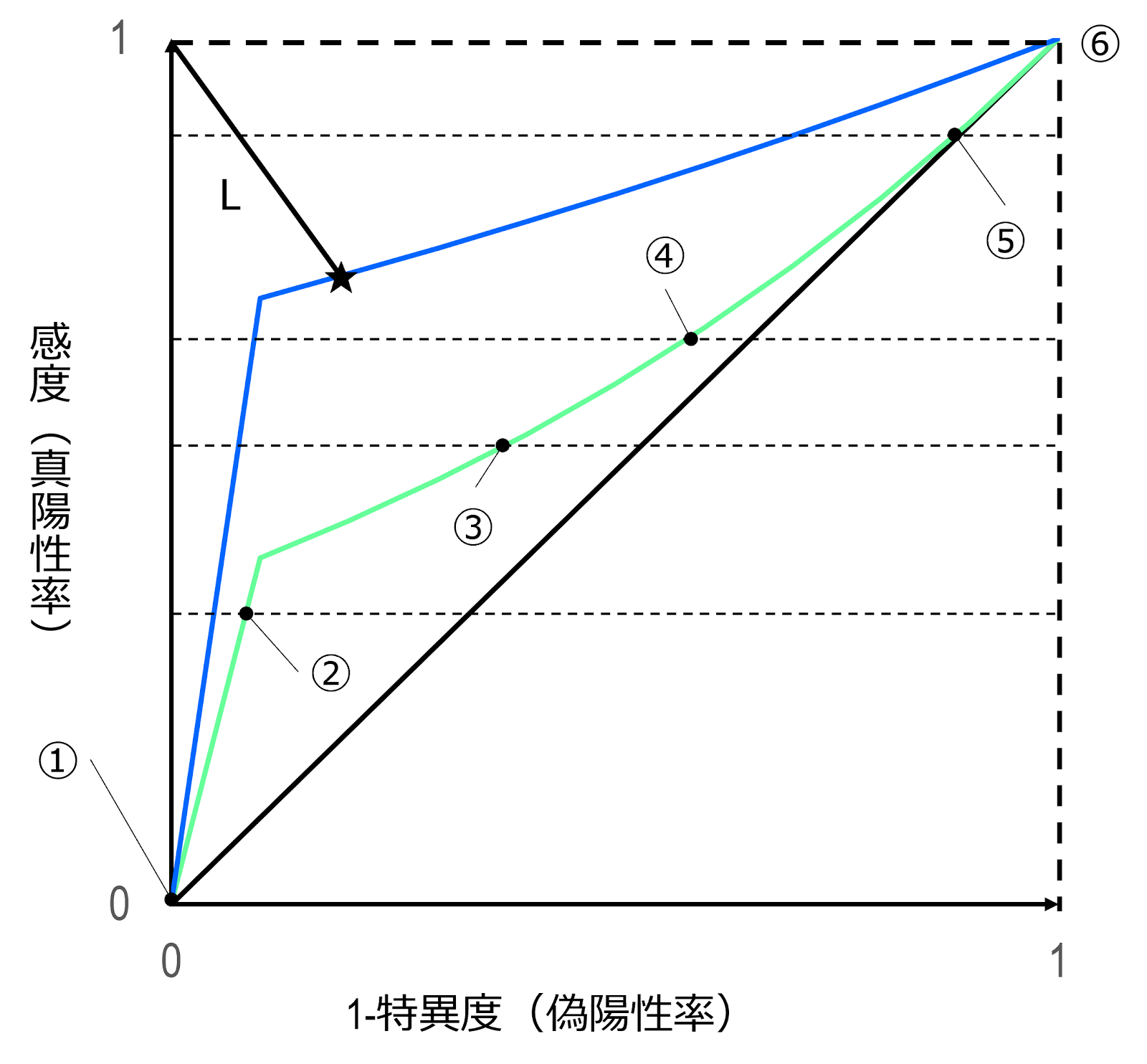
診断検査の性能を考えると、「有病者全員を陽性とし、無病者を全員陰性にする」、すなわち、「感度(真陽性率)が100%、偽陽性率が0% の検査」が理想的な検査となります。このグラフの中では座標 $ \left(0,1\right)$ がそれにあたる点です。
いっぽう、原点 $ \left(0,0\right)$ と $ \left(1,1\right)$ を結ぶ対角線上にある点をカットオフ値とする場合、それは、実質的に行う意味のない検査ということになります。対角線上の点は、すなわち真陽性率=偽陽性率となる点ということです。ここから、陽性的中度を求めると、 \begin{gather} \mathrm{\widehat{PPV}}=\frac{P \left(+\cap D\right)}{P \left(+\right)}=\frac{P \left(+\cap D\right)}{P \left(+\cap D\right)+P \left(-\cap D\right)}=\frac{x}{x+x}=\frac{1}{2} \end{gather} これは、「コインを投げて、表ならその人は有病者、裏なら無病者」と判定する場合と実質的に同じことになってしまい、意味がありません。
つまり、カットオフ値は、最低でも対角線よりも上にあることが必要で、座標 $ \left(0,1\right)$ に近いほど、感度と特異度のバランスが取れていて、総合的な識別性能が高いということになります。このことから、ROC 曲線と $ \left(0,1\right)$ までの距離 L が最短になるような点★に対応するようにカットオフ値を定めるという方法が、閾値を決定するうえでのひとつの目安とすることができます。
ROC曲線による検査どうしの比較
ROC曲線は、複数の検査性能を比較する際にも用いることができます。先の話では、ROC 曲線と $ \left(0,1\right)$ までの距離が近いほど良いということでしたが、これを定量的に表現する指標に曲面下面積があります。
曲面下面積 area under curve: AUC とは、ROC曲線、$x$ 軸、および直線 $x=1$ で囲まれる領域の面積のことです。AUCの最大値は、ROC曲線が $y=1$ となる場合、辺の長さが1の正方形の面積なので、1です。いっぽう、最小値は、ROC曲線が対角線に一致する(無意味な検査である)場合、底辺と高さが1の直角二等辺三角形の面積なので、0.5です。
このAUCを計算し、その値が大きい方が平均的に優れた検査ということになります。
検査の目的とカットオフ値
ただ、こうしたカットオフ値の決め方は、あくまでも決め方のひとつで、実際には、その検査の目的に応じて決める必要があります。この点、結論を先取りすると、一般的に、感度が高い検査は、稀な疾患に対する「除外診断(スクリーニング検査)」に、特異度が高い検査は、その疾病に対する「確定診断」にそれぞれ向いています。
感度が高い検査とは、有病者の中で陽性となる割合が高い=有病者の中で陰性となる割合が低い=偽陰性が小さいということであり、偽陰性が真陰性より相対的に小さくなるので、陰性的中率が高くなります。つまり、表2の例で見たように、陰性の結果の信頼性が高く、陰性者はほぼ無病者と断言できるということなので、稀な疾患に対する除外診断、つまり、健康診断のようなマス・スクリーニングで疾患発見を目的とするような場合に向いています。
いっぽう、特異度が高い検査とは、無病者の中で陰性となる割合が高い=無病者の中で陽性となる割合が低い=偽陽性が小さいということであり、偽陽性が真陽性より相対的に小さくなるので、陽性的中率が高くなります。例えば、表3のような妊娠検査の場合を考えてみると、付帯状況が存在しなければ、あえて検査を受ける人は少ないと思われるので、事前確率はおそらく高いと考えられます。仮に妊娠している事前確率を50%とすると、感度と特異度がそれぞれ90% と99% である場合、陽性的中度・陰性的中度は、 \begin{gather} \mathrm{\widehat{PPV}}=\frac{90}{91}\cong98.9\%\\ \mathrm{\widehat{NPV}}=\frac{99}{109}\cong90.8\% \end{gather} となります。 すなわち、陽性であれば、ほぼ確実に妊娠しているということになります。
| 陽性 $ \left(+\right)$ | 陰性 $(-)$ | 合計 | |
|---|---|---|---|
| 妊娠あり $ \left(D\right)$ | $90$ | $10$ | $100$ |
| 妊娠なし $(\bar{D})$ | $1$ | $99$ | $100$ |
| 合計 | $91$ | $109$ | $200$ |
こうしたことから、特異度が高い検査は、有病率が高いと考えられる集団に対し、本当にその疾病があるか否かを確認することを目的として行う確定診断に向いています。
このように、その診断検査の目的に応じて、感度が高くなるようにカットオフ値にするのか、それとも特異度が高くなるようなカットオフ値とするのかを決めることが大切です。
予後との関係から見た診断検査の評価:3つのバイアス
最後に、予後との関係から見た診断検査の評価について考えたいと思います。診断検査の中でも定期健診などのスクリーニング検査は、早期発見・早期治療を目的として行われ、疾病を発見した後の生存率や生存時間という観点からも、その有用性の評価を行うことができそうです。しかし、このような場合、リードタイム・バイアス、レングス・バイアス、自己選択バイアスという3つのバイアスに注意しなければなりません。
リードタイム・バイアス
リードタイム・バイアス leadtime bias とは、疾患の自然史が同じ場合でも、スクリーニングによって疾病が発見された方が、観測される生存時間が長くなるということです。これは、発見したとしても、手の施しようがない状態だった場合を考えると理解しやすいと思われます。
例えば、がんの場合を考えます。がんの治療成功率は通常、診断後の生存期間や再発までの期間で測定します。もし早期治療が有効なら、生存期間や再発までの期間は延びると予想されます。しかしスクリーニングを行うと、スクリーニングや早期治療が無意味な場合でも、生存期間や再発までの期間は延びます。これはスクリーニングにより診断時期が前に動くために、スクリーニングを行わなかった場合と比較して、疾患の自然経過における診断時期が早まるからです。
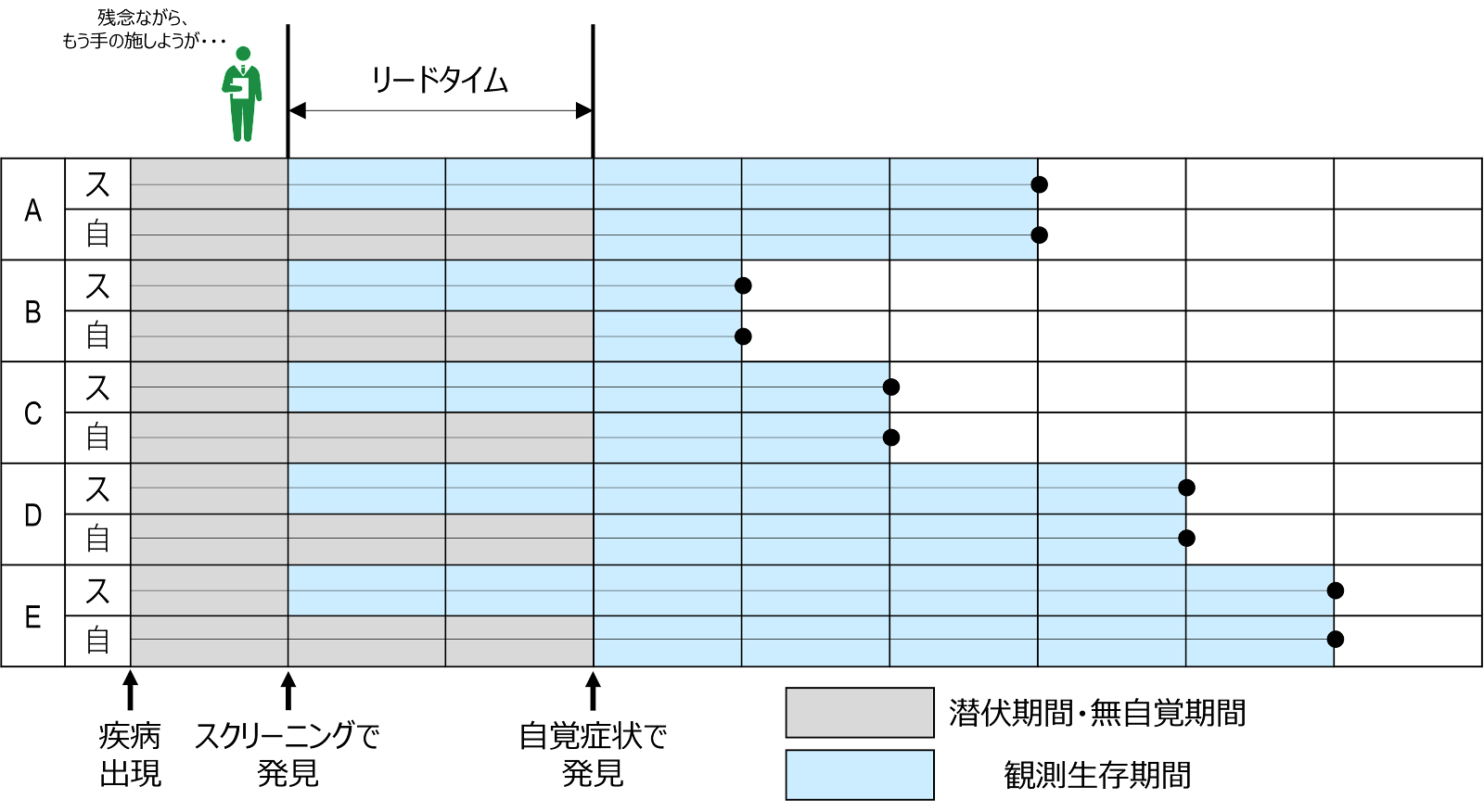
スクリーニングを行った場合と行わなかった場合の診断日時の時間差はリードタイム leadtime と呼ばれます。ただ、リードタイムは見かけ上存在するだけで実際の利益を何ももたらさないため、診断後の生存期間に含めても、実質的な意味はありません。もしリードタイムを含めて考えると、その分、見かけ上、生存時間=治療成績が良いように見えるという意味で、それがバイアスとなってしまいます。
レングス・バイアス
レングス・バイアス length bias とは、進行が遅い疾病ほどスクリーニングで発見される確率が高く、進行が速い疾病ほど見逃される確率が高いということです。これは、スクリーニングで発見できる疾病は、もともと比較的予後が良いものである確率が高いといいかえることもできます。
再び、がんを例にしましょう。話を単純化するため、進行の早いがんと遅いがんの2種類があるとします。進行の早いがんは、つまりがんが発生してから死亡に至るまでの時間が短く、遅いがんは、死亡までに長い時間がかかります。スクリーニングは、基本的に自覚症状がなく、健康であると思われるときに受けるものですが、病気の進行が速い場合は、あっという間に自覚症状が出て、スクリーニングを受けるチャンスもないままに治療を開始するか、悪くすれば、死んでしまいます。それに対し、進行が遅い場合は、「前回は見逃されたにもかかわらず、今回は発見できた」ということもあり得ます。この間も病状は進行していますが、まだ死んでしまうほどではなく、進行が速い場合と比べると、相対的に良性ということになります。
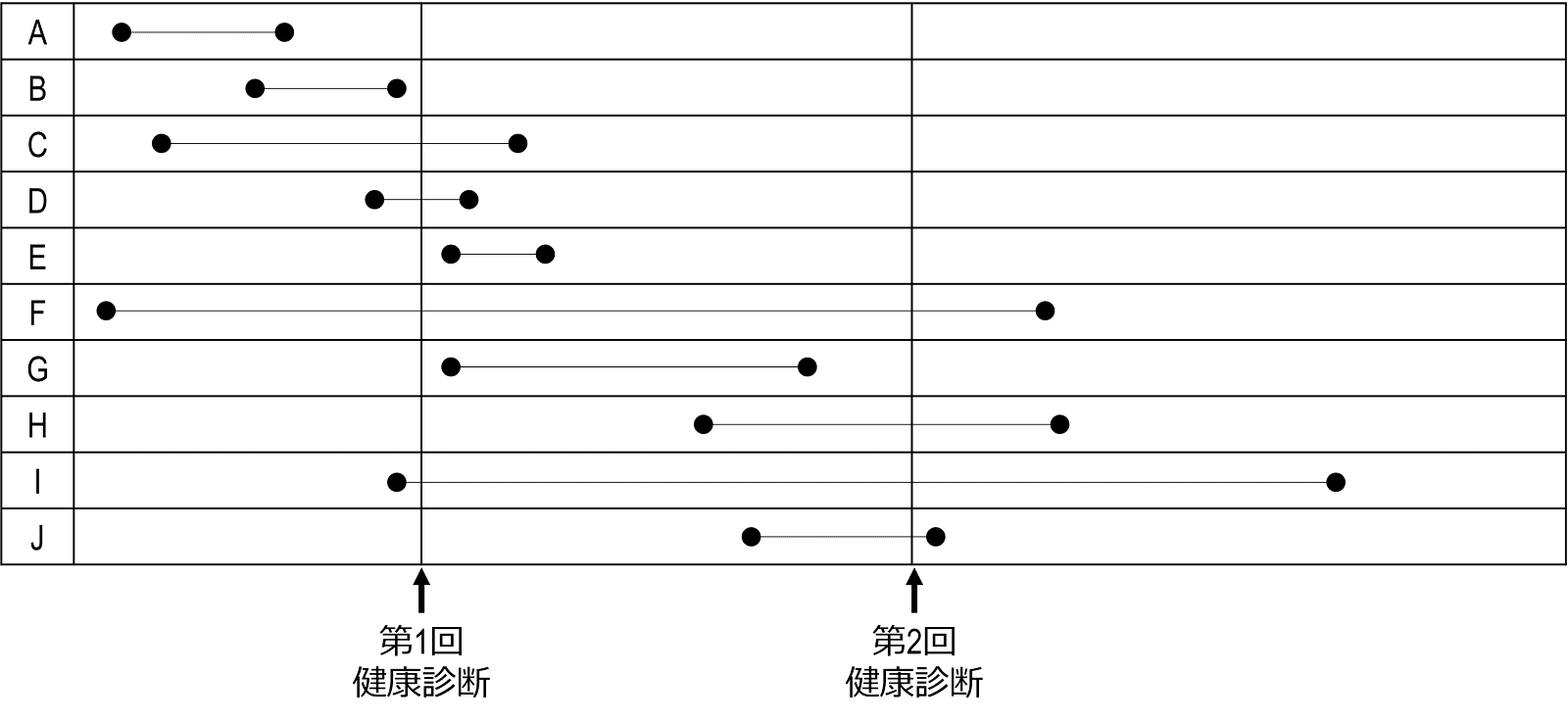
このように、進行の早いがんにかかっている患者は、進行の遅いがん患者よりも予後が悪くなる傾向にあります。進行の早いがんでは前臨床段階から臨床段階へとすみやかに移行し、広がるのも早く、多くの思者が早くに死に至ります。進行の遅いがんはより良性で、前臨床段階から臨床段階に進行するのに数ヶ月、数年もかかります。進行の遅いがん患者の予後は、進行の早いがん思者と比較して治療をしなくても良好ですが、治療をした場合はより効果がある可能性も高くなります。この意味で、スクリーニングによって発見された例は、治療成績が良くなりやすいという方向にバイアスがかかっていると考えられます。
自己選択バイアス
自己選択バイアス self-selection bias、あるいは予後選択パイアス prognostic selection bias とは、予後が悪化する可能性がスクリーニング受検者の集団と一般集団とで異なる可能性があるということです。これは、スクリーニング検査を受ける人は、もともと健康的である場合があるということです。
定期健診などのスクリーニング・プログラムへの参加は、基本的に任意で自発的なものです。そのため、スクリーニングの任意受診者はスクリーニングを受けなかった人とさまざまな点で異なる可能性があります。最も典型的な例は、「スクリーニングの受診者は、健康への意識が高く、日ごろから健康に気を遣った生活を送っていて、スクリーニング検査もその一環として受診する」というものです。
例えば、お酒も飲まないしタバコも吸わない人がスクリーニングを受けて、ごく初期のがんが発見されたという場合と、酒もタバコも止められない人が面倒がってスクリーニングを受けず、自覚症状が出てからがんが発見されるという場合では、前者の方が、予後が良好になることは想像に難くありません。このような場合、スクリーニング受診者から発見される疾患は、非参加者(=自覚症状発見群)から発見されるものとは性状が異なる可能性があります。
このようなバイアスを克服する最もよい研究方法は、無作為化試験(介入研究)で評価することです。すなわち、対象者を無作為に2群に分け、介入群にはスクリーニングを積極的に受けさせ、対照群とのその後の死亡率や重症化の頻度を比較するという方法で真のスクリーニングの有効性が確認できます。
参考文献
- ダグラス・アルトマン 著, 木船 義久, 佐久間 昭 訳. 医学研究における実用統計学. サイエンティスト社, 1999, p.329-337
- ケネス・ロスマン 著, 矢野 栄二, 橋本 英樹, 大脇 和浩 監訳. ロスマンの疫学:科学的思考への誘い. 篠原出版新社, 2013, p.327-335
- スティーブン・ハリー, スティーブン・カミングス ほか 著, 木原 雅子, 木原 正博 訳. 医学的研究のデザイン:研究の質を高める疫学的アプローチ. 第4版, メディカル・サイエンス・インターナショナル, 2014, p.198-216
- 丹後 俊郎, 松井 茂之 編集. 医学統計学ハンドブック 新版. 朝倉書店, 2018, p.653-673
- 中村 好一 著. 基礎から学ぶ楽しい疫学. 医学書院, 2020, p.132-142
- 大野 良之. 疫学と統計学の基礎講座: スクリーニングテストの妥当性とROC曲線. 日本循環器管理研究協議会雑誌. 1990, 25(2), p.111-113, doi: 10.11381/jjcdp1974.25.111
- 小柳 貴裕. 統計学 整形外科医が知っておきたい(04)診断能力の評価:感度・特異度のジレンマ. 臨床整形外科. 2002, 37(6), p.735-741.
- 大橋 靖雄. 医師のための臨床統計学: (03)検査データの解釈―ベイズ統計学入門. 医学のあゆみ. 2008, 227(11), p.1013-1020.
- 柳橋 達彦. 診断検査の特性の評価. 小児科診療. 2009, 72(4), p.659-665.
- 嘉田 晃子. 診断法の開発はどのように行うか. 医学のあゆみ. 2013, 244(13), p.1253-1257.
脚注
- 日本語では「率」で定着していますが、疫学の定義上は「割合」の意味です。
- 例えば、有病率が1%であれば、すべてを「陰性」とすれば正診率は99%にできます。
- ROC曲線の英語名称を訳すと、「受信者操作特性曲線」ということになります。この概念は、もともとレーダー技術の分野から生まれたもので、第二次世界大戦で開発されたレーダー上に現れたシグナルを、船・飛行機の影ととるか雲などの撹乱情報ととるかの判断が、オペレータによって異なったそうです。この現象をオペレータの「閾値」の違いで説明したことから、このように命名されたといわれています。



0 件のコメント:
コメントを投稿