科学研究などの場面において、さまざまな説明変数の値から、関心のある応答変数の値を予測するために、回帰分析が行われることがあります。そのうち、応答変数がカテゴリー変数の場合に用いられるのがロジスティック回帰分析です。本稿では、そうしたロジスティック回帰分析の概要について解説しています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
回帰モデルによる目的変数の予測
人文・社会科学や医薬・生物学などさまざまな科学分野において、それぞれの個体がもっている共変量(説明変数)の値から、関心のある応答変数(目的変数)の値を予測するために、回帰分析が行われることがあります。例えば、「身長 $X$」から「体重 $W$」を予測する、「年齢 $X_1$」と「身長 $X_2$」と「体重 $X_3$」から「血圧 $Y$」の値を予測するというような場合です。前者のように、共変量(説明変数)が1つの場合を「単回帰」、共変量(説明変数)が2つ以上の場合を「重回帰」と呼びます。このとき、 \begin{gather} W=\alpha+\beta X\tag{1}\\ Y=\alpha+\beta_1X_1+\beta_2X_2+\beta_3X_3\tag{2} \end{gather} という 回帰モデルを考え、実際に得られたデータから回帰係数や偏回帰係数を推定します。そして、完成したモデル式に説明変数の値を代入することで、実際には得られなかった値の組み合わせにおいても、応答変数の値を予測できるようにするというのが回帰分析の基本的な発想でした。
例えば、「1日あたりの喫煙本数 $X$(本)」から「咽頭がんによる年齢標準化死亡率 $Y$(100000人・年)」を予測するモデルとして、 \begin{gather} \hat{Y}=1.15+0.282X \end{gather} という回帰直線が考えられるとします$^\mathrm{(1)}$。 このとき、切片 $\alpha=1.15$ は、喫煙数が $X=0$ のときの死亡率の予測値を表しており、回帰係数 $\beta=0.282$ は、毎日タバコを1本多く吸うことにより、100000人・年あたりの死亡者数が $0.282$ 上昇することを示しています。交絡と他のバイアスが適切に取り扱われたとすれば、回帰直線の傾きは喫煙が喉頭がんに与える効果を定量化したものとなります。
また、回帰直線から、他の喫煙レベルにおける死亡率も推定することができます。たとえば、1日50本タバコを吸う人の死亡率は回帰直線から100000人・年あたり \begin{gather} \hat{Y}=1.15+0.282 \cdot 50=15.25 \end{gather} と推定できます。 これを非喫煙者の推定値100000人・年あたり1.15と比較してみると、1日に2.5箱吸う人の死亡率比は \begin{align} \mathrm{IRR}=\frac{15.25}{1.15}\cong13.3 \end{align} となり、 喫煙本数が喉頭がん死亡率に強い影響があることを理解することができます。
なお、単回帰分析や重回帰分析は、基本的に、目的変数 $Y$ が、血圧や肺活量などの連続値(間隔尺度・比尺度)である場合に用いられます。共変量については、身長や体重などの連続値、「良い」、「中立」、「悪い」などの順序尺度、「薬の服用あり・なし」や「A型」、「B型」、「O型」、「AB型」、「その他」などのカテゴリー変数(名義尺度)のいずれも用いることができます。
重回帰分析は、例えば、ある疾患と関連のある臨床検査値について、「年齢」と「飲酒量」が悪い影響(値が大きいほど、検査値が高くなる)を与えるとしたとき、「若いけど、よく飲酒する人」と「高齢だけど、飲酒しない人」であれば、どちらの方が検査値が良くなるのかといった疑問に対し、2つの因子の影響を同時に加味した値を予測できること、あるいは、偏回帰係数を調べることで、「飲酒量」の影響を取り除いた、「年齢」単独の影響を定量化できる点などが利点とされています。
応答変数がカテゴリー変数の場合
ただ、医薬・生物学の分野では、死亡や疾病の再発といったイベント発生の「あり・なし」、あるいは健康状態の「良い」、「中立」、「悪い」などのカテゴリー変数を扱うことがよくあります。話を先取りすれば、応答変数が3つ以上のカテゴリー変数である場合は、多項ロジスティック回帰 polytomous (multinomial) logistic regression、順序尺度である場合は、順序ロジスティック回帰 ordinal logistic regression という手法を使うことになりますが、ここでは最も基本的な場合である、イベント発生の「あり・なし」の二値変数の場合を考えます。
例えば、5年後にある疾病を発症するかどうかをコホート研究で調べた結果、発症ありを1、発症なしを0として、以下のようなデータが得られたとします$^\mathrm{(2)}$。そして、このデータを用いて、現在の年齢 $X$ を説明変数として、5年後にある疾病を発症するかどうか $Y$ を予測したいとします。
| No. | 年齢 | 発症 |
|---|---|---|
| 1 | $18$ | $0$ |
| 2 | $21$ | $0$ |
| 3 | $22$ | $0$ |
| 4 | $25$ | $0$ |
| 5 | $26$ | $0$ |
| 6 | $28$ | $0$ |
| 7 | $33$ | $0$ |
| 8 | $34$ | $0$ |
| 9 | $35$ | $0$ |
| 10 | $37$ | $0$ |
| 11 | $42$ | $1$ |
| 12 | $47$ | $1$ |
| 13 | $55$ | $0$ |
| 14 | $56$ | $1$ |
| 15 | $58$ | $0$ |
| 16 | $61$ | $1$ |
| 17 | $65$ | $1$ |
| 18 | $68$ | $1$ |
| 19 | $75$ | $1$ |
| 20 | $77$ | $1$ |
このデータに単純に線形回帰モデルを適用すると、 \begin{gather} \hat{Y}=-0.49+0.02X \end{gather} という回帰式を得ることができます。
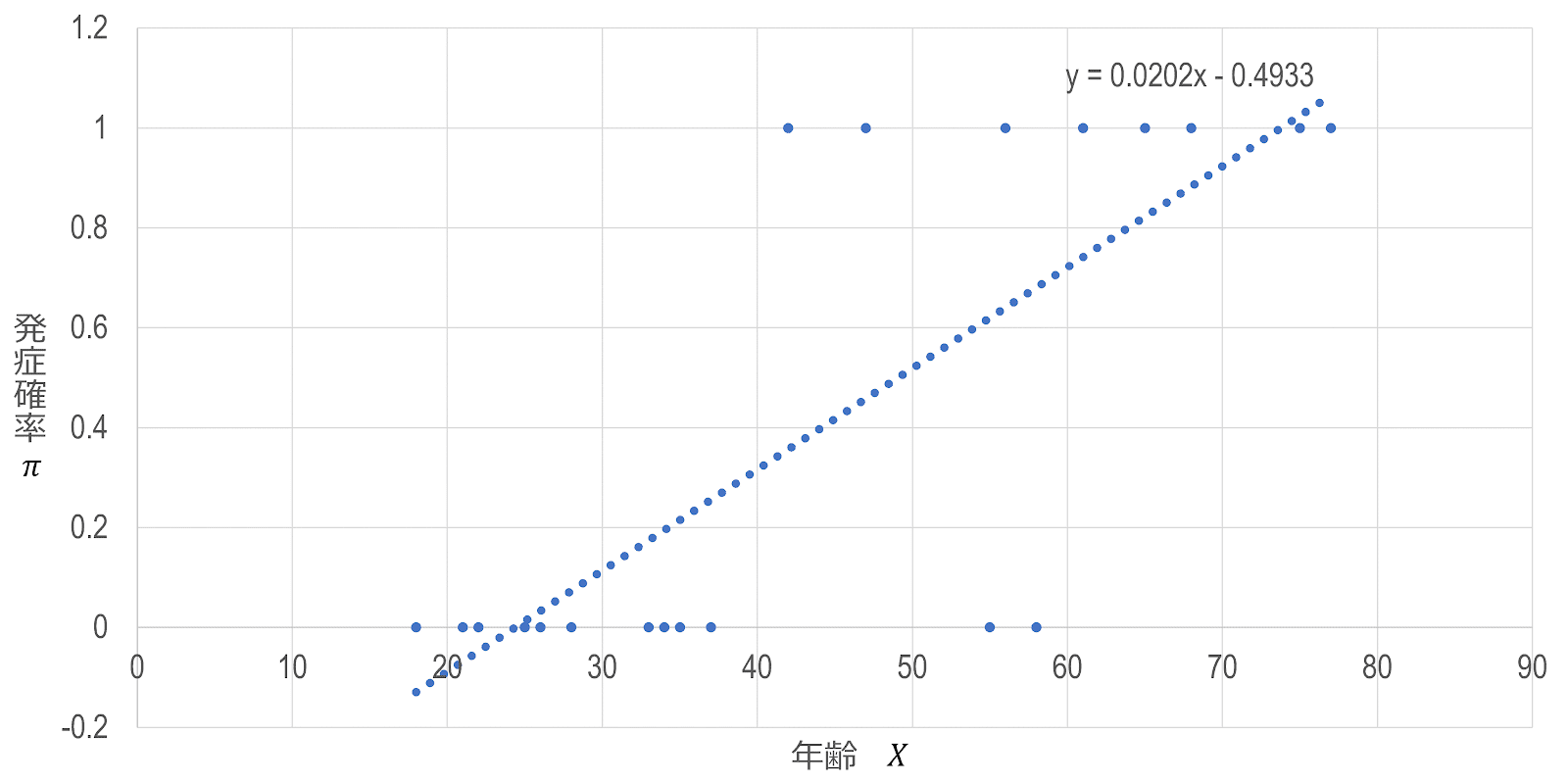
しかし、この回帰式を解釈しようとすると、いくつかの問題に行き当たることに気づきます。
まず、応答変数 $\hat{Y}$ の値の意味についてです。問題となっている予測モデルでは、発症ありを1、発症なしを0としているため、予測値が0か1であれば、それぞれ「発症しない」、「発症する」という予測であることになりますが、実際にはそのような点はそれぞれ1点ずつしかなく、むしろ $0 \lt Y \lt 1$ となる点が無数に存在します。この点、回帰分析における応答変数の予測値は厳密には、「説明変数の値が $x$ であるときの応答変数の期待値」であることを考えると、二値応答における期待値、すなわち、その事象が発生する確率を意味することになります。
ただ、応答変数 $\hat{Y}$ を確率として解釈するというのはいいとしても、もう1つ大きな問題があります。例えば、この回帰式において $X=20$ や $X=80$ という値を代入すると、それぞれ $\hat{Y}=-0.09,\hat{Y}=1.12$ という値になってしまいます。確率の基本性質より、$\hat{Y}$ の値の範囲は、$0 \le \hat{Y} \le 1$ であるため、負の値や1以上の値は取ることができませんが、この回帰モデルにおいては、予測値がそのような「取り得ない値」を取ることができてしまい、こうした場合、その意味を解釈したり定義したりすることができなくなってしまいます$^\mathrm{(i)}$。
ロジスティック回帰モデル
この問題は、回帰式の左辺と右辺で、取り得る値の範囲が同じでないことに起因します。左辺は確率であるため、$\hat{Y}\in \left[0,1\right]$ ですが、$X$ がすべての実数を取るとすれば$^\mathrm{(ii)}$、右辺はすべての実数を取り得ることになります($X\in \left[-\infty,\infty\right]\Rightarrow\alpha+\beta X\in \left[-\infty,\infty\right]$)。それゆえに、何かしらの工夫をすることで、この問題を解消する必要があります。
この点、結論を言ってしまえば、左辺の応答変数の表現を工夫します。具体的には、まず、問題としている疾病の発症確率 $\pi$ を考えるのではなく、発症オッズ $\frac{\pi}{1-\pi}$ について考えます。そうすると、 \begin{gather} \pi=0\Rightarrow\frac{\pi}{1-\pi}=\frac{0}{1-0}=0\\ \pi=0.5\Rightarrow\frac{\pi}{1-\pi}=\frac{0.5}{1-0.5}=1\\ \pi=0.9\Rightarrow\frac{\pi}{1-\pi}=\frac{0.9}{1-0.9}=9\\ \pi\rightarrow1\Rightarrow\lim_{\pi\rightarrow1}{\frac{\pi}{1-\pi}}=\infty\\ \end{gather} すなわち、 \begin{gather} \frac{\pi}{1-\pi}\in \left[0,\infty\right] \end{gather} となり、目標に少し近づきます。 右辺は、負の値も取り得えますが、発症オッズの対数を取ることによって、この点に応えることができます。すなわち、 \begin{gather} \pi\rightarrow0\Rightarrow\lim_{\pi\rightarrow0}{\log{\frac{\pi}{1-\pi}}}=-\infty\\ \pi\rightarrow1\Rightarrow\lim_{\pi\rightarrow1}{\log{\frac{\pi}{1-\pi}}}=\infty \end{gather} ということです。
つまり、一般的に $k$ 個の共変量と対応する $k+1$ 個の回帰係数 \begin{align} \boldsymbol{X}= \left\{\begin{matrix}X_1\\X_2\\\vdots\\X_k\\\end{matrix}\right\} \quad \boldsymbol{\theta}= \left\{\begin{matrix}\alpha\\\beta_1\\\vdots\\\beta_k\\\end{matrix}\right\} \end{align} があるとき、 \begin{gather} \log{\frac{\pi}{1-\pi}}=\alpha+\beta_1X_1+\beta_2X_2+ \cdots +\beta_kX_k=\alpha+\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}\tag{3} \end{gather} という 回帰モデルを考えると、重回帰分析とほぼ同じ発想で予測をすることができるということになります。式 $(3)$ の左辺、対数オッズは、特にロジット logit と呼ばれ、 \begin{gather} \log{\frac{\pi}{1-\pi}}=\mathrm{logit} \left(\pi\right) \end{gather} と表されることもあります。 また、重回帰での偏回帰係数に相当する $\beta$ は、ロジスティック回帰ではロジスティック回帰係数 logistic regression coefficient と呼ばれることがあります。
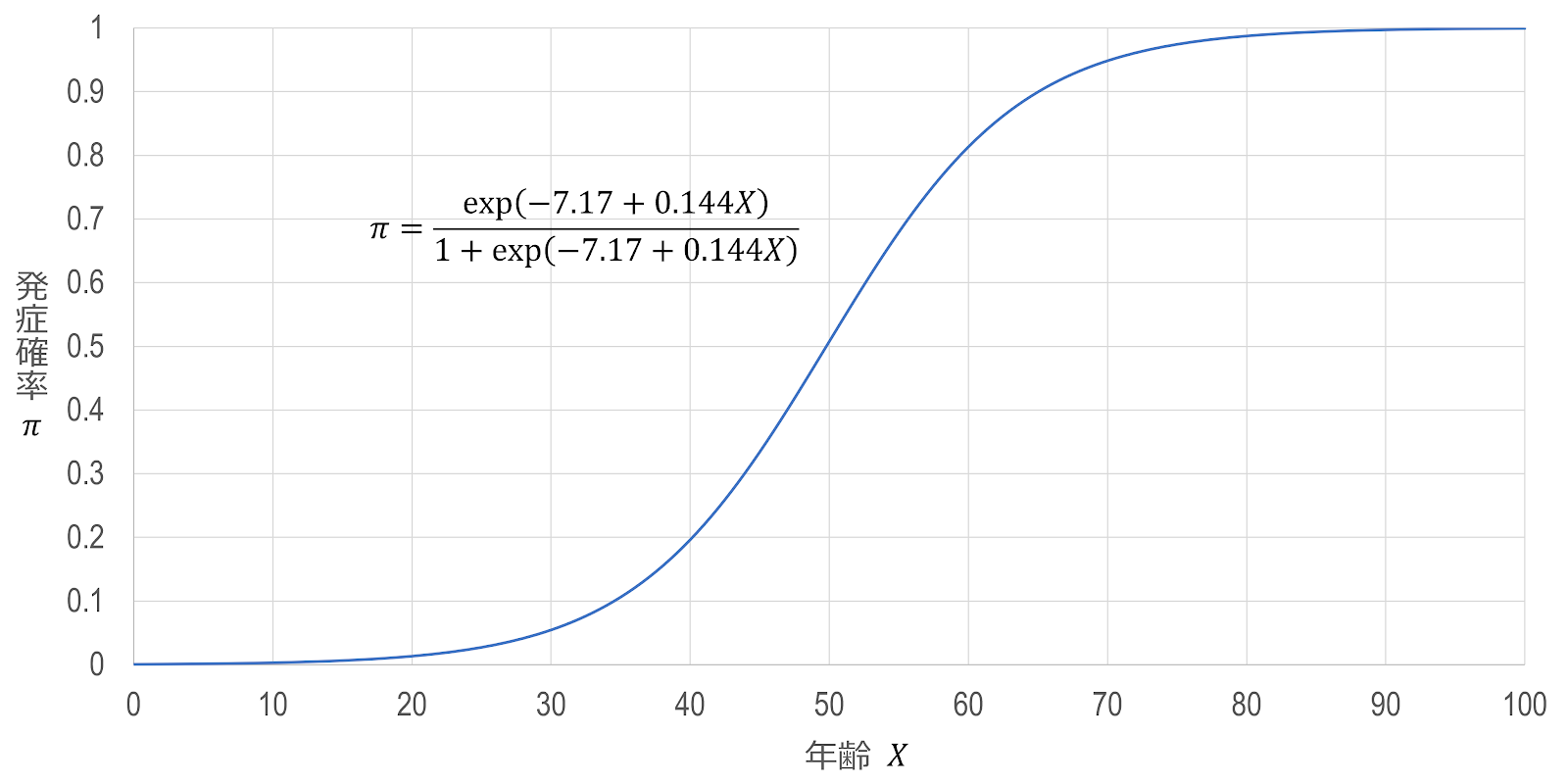
また、式 $(3)$ を変形すると、 \begin{gather} \frac{\pi}{1-\pi}=e^{\alpha+\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}}\\ \pi=e^{\alpha+\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}} \left(1-\pi\right)\\ \pi \left(1+e^{\alpha+\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}}\right)=e^{\alpha+\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}}\\ \pi=\frac{e^{\alpha+\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}}}{1+e^{\alpha+\boldsymbol{x}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{\beta}}} \end{gather} となります。 この関数はロジスティック関数と呼ばれているため、回帰モデルがロジスティック回帰モデル logistic regression model と呼ばれています。ロジスティック回帰モデルは、オッズ比を用いる回帰モデルであるため、もともとオッズ比を指標として用いるケース・コントロール研究と相性が良く、ケース・コントロール研究でよく用いられています。
今回の例で、ロジスティック回帰モデルを適用した場合、予測値のグラフは以下のようになります。
ロジスティック回帰分析の歴史と意義
ロジスティック回帰分析は、疾患のリスク因子を分析するためによく用いられています。ロジスティック関数の使用などに遡れば、歴史的には、新しい手法ではありませんが、1948年にアメリカのフラミンガムで開始されたフラミンガム研究の分析のために用いられたことによって、その有用性が一般に広まったという経緯があります$^\mathrm{(3)}$。
当時の疫学は、もともと疫学研究がコレラ菌という病原菌への対策として始まったなどの経緯があったことから、病因概念として定着していたのは原因としての「病原菌」、結果としての疾病の「発症」という1:1の因果関係でした。つまり、病原菌に曝露されていなければ、感染症は発症しないということになるわけですが、がん、糖尿病、循環器疾患のような疾患は、さまざまな要因が複雑に絡み合って発症するかしないかが決まります。つまり、発症リスクがまったくの0という人は厳密にはほとんど存在せず、危険因子(共変量)の組み合わせによって、高リスクの人もいれば、低リスクの人もいるという場合の方が多いでしょう。そのような危険因子の組み合わせを多重リスクファクター multiple risk factor という概念によって捉え、複雑に影響し合う危険因子の影響を同時に考えるという発想がロジスティック回帰分析の開発によって生まれました。
この方法の波及効果は大きく、7ヵ国共同疫学調査をはじめとして、これ以後の冠状動脈性心疾患に関する疫学調査のほとんどすべてが、この方法を利用してリスクファクターの評価を行っています。また、もう1つの重要な貢献は、これらの成果によって、疾患予防対策を感染症とは全く異なった方法で実現できたことです。このフラミンガム調査をきっかけとして世界的に行われた疫学調査の結果により、たとえば、虚血性心疾患でいえば、その1次予防として、高脂肪食品の制限、血圧スクリーニング、禁煙キャンペーン、が確立していきました。
回帰係数の意味
重回帰での偏回帰係数は「ほかの変数が動かず、その変数だけ1単位変化したとき、予測先の変数はいくつ変化するか?」を示していました。では、ロジスティック回帰係数はどうでしょうか?
この点、実際に検証してみると、例えば、以下のような単純なモデルが成り立つとします。 \begin{gather} \log{\frac{\pi_i}{1-\pi_i}}=\alpha+\beta_1X_1+\beta_2X_2 \end{gather} この式で共変量 $X_1$ が女性なら0、男性なら1を取る二値変数であるとし、共変量 $X_2$ の値は等しく、性別だけが違う2人を考えます。このとき、女性のオッズは、 \begin{gather} \log{\frac{\pi_0}{1-\pi_0}}=\alpha+\beta_1 \cdot 0+\beta_2X_2=\alpha+\beta_2X_2 \end{gather} 男性のオッズは、 \begin{gather} \log{\frac{\pi_1}{1-\pi_1}}=\alpha+\beta_1 \cdot 1+\beta_2X_2=\alpha+\beta_1+\beta_2X_2 \end{gather} これらの差を取ると、 \begin{gather} \log{\frac{\pi_1}{1-\pi_1}}-\log{\frac{\pi_0}{1-\pi_0}}=\alpha+\beta_1+\beta_2X_2-\alpha+\beta_2X_2=\beta_1\\ \log{\frac{\frac{\pi_1}{1-\pi_1}}{\frac{\pi_0}{1-\pi_0}}}=\beta_1\\ \log{\mathrm{OR}}=\beta_1\\ \mathrm{OR}=e^{\beta_1} \end{gather} となります。 すなわち、一般に回帰係数 $\beta_i$ は、他の共変量の値が共通しているときに、対応する共変量 $X_i$ を1単位変化させたときの対数オッズ比であり、その指数を取った値 $e^{\beta_i}$ は、オッズ比ということになります。この場合は、希少疾患の仮定の下で、男性は女性に比べて、$e^{\beta_1}$ 倍の発症リスクを有しているということを示しています。
ロジスティック回帰モデルを用いた交絡の調整
ケース・コントロール研究を実施する際、交絡が問題となることがあります。交絡とは、影響を調べている因子Aとアウトカムの両方に影響を与える第3の因子Bの分布が、因子A の曝露群と非曝露群で異なる場合に、見かけ上、因子Aとアウトカムの間に関連があるように(もしくは、ないように)見えてしまう現象のことです。例えば、喫煙と脳卒中の関係について調べた結果、以下のようになったとします$^\mathrm{(4)}$。
| 喫煙あり | 喫煙なし | 合計 | |
|---|---|---|---|
| 脳卒中あり | $98$ | $159$ | $257$ |
| 脳卒中なし | $64$ | $211$ | $275$ |
曝露オッズ比 \begin{align} \mathrm{\widehat{OR}}=\frac{98\times211}{64\times159}=2.032 \end{align}
この結果は、ロジスティック回帰モデルを用いることによっても、同じ結果を得ることができます。具体的には、喫煙の有無のみを共変量 $X_1$ とした、単変量の \begin{gather} \log{\frac{\pi_i}{1-\pi_i}}=\alpha+\beta_1X_1 \end{gather} というモデルの回帰係数を推定することによってです。
得られたデータから、切片と回帰係数を推定すると、 \begin{gather} \log{\frac{\pi_i}{1-\pi_i}}=-0.2830+0.7090X_1\\ \mathrm{\widehat{OR}}=e^{0.7090}=2.032 \end{gather} となります。 このように、ある共変量に関して、層別化などをすることなく単純に求めたオッズ比を粗オッズ比と呼びます。しかし、これが例えば「年齢」などの因子が交絡因子となり、この結果が歪められている可能性があるということです。そうした交絡の影響を調整するために、層別解析などの手法が用いられることもありますが、先に見た回帰係数の性質を用いると、ロジスティック回帰モデルでも、交絡の調整ができることが分かります。
やり方は単純に、交絡因子となりそうな共変量をモデルに組み込み、式 $(3)$ の \begin{gather} \log{\frac{\pi}{1-\pi}}=\alpha+\beta_1X_1+\beta_2X_2+ \cdots +\beta_kX_k \end{gather} というモデルを想定し、 それぞれの回帰係数を推定するという方法です。
この結果、例えば、 \begin{gather} \log{\frac{\pi_i}{1-\pi_i}}=-2.7943+0.7809X_1+ \cdots +\beta_kX_k\\ \mathrm{\widehat{OR}}=e^{0.7809}=2.183 \end{gather} となれば、 交絡因子の影響を取り除いた「喫煙」単独の影響は「発症リスクを2.183倍にする」というものであることを表しています。このように、交絡因子の影響を取り除いた後のオッズ比を調整済みオッズ比と呼びます。
ロジスティック回帰係数の推定と検定
線形回帰分析の場合、偏回帰係数は最小2乗法で推定されますが、ロジスティック回帰分析の文脈では、最小2乗法を使って推定値を算出することができないため、ニュートン・ラフソン法などの反復計算にもとづく最尤法という方法によって、回帰係数の推定値を求めます。この計算は、非常に複雑で人の手にはとても負えないので、統計パッケージなどのコンピューターソフトを用いる必要がありますが、その計算の理論的背景の概要は、以下のようになっています。
ロジスティック回帰モデルにおいて、$P \left(Y=1\right)=\pi,P \left(Y=0\right)=1-\pi$ となる確率はそれぞれ、 \begin{gather} \pi=\frac{e^{\alpha+\beta x}}{1+e^{\alpha+\beta x}} \quad 1-\pi=\frac{1}{1+e^{\alpha+\beta x}} \end{gather} となります。 $n$ 個の無作為標本において $Y=1$(イベント発生あり)となる人が $d$ 人いれば、$Y=0$(イベント発生なし)となる人は $n-d$ 人なので、この標本が得られる尤度 $L$ は、二項確率により、 \begin{gather} L \left(\pi\right)={}_{n}C_d\pi^d \left(1-\pi\right)^{n-d}\\ L \left(\pi\right)={}_{n}C_d \left(\frac{e^{\alpha+\beta x}}{1+e^{\alpha+\beta x}}\right)^d \left(\frac{1}{1+e^{\alpha+\beta x}}\right)^{n-d} \end{gather} となり、 ここからニュートン・ラフソン法などの反復計算によって、$\beta$ の推定値 $\hat{\beta}$ を算出します。
また、最尤推定量 $\hat{\beta}$ が漸近的に正規分布に従うことを用いると、推定量の分散を $V \left(\hat{\beta}\right)$ として、以下の尤度比検定(ワルド検定)統計量は、 \begin{gather} \chi_W^2=\frac{{\hat{\beta}}^2}{V \left(\hat{\beta}\right)} \sim \chi^2 \left(1\right) \end{gather} となります。 これを用いると、ロジスティック回帰係数について、 \begin{gather} H_0:{\hat{\beta}}_i=0 \quad \mathrm{v.s.} \quad H_1:{\hat{\beta}}_i \neq 0 \end{gather} の仮説検定を行うことができます。 また、重回帰分析と同様、ロジスティック回帰係数についても、推定量の標準誤差 $\mathrm{S.E.} \left(\hat{\beta}\right)$ を用いて以下のように、信頼区間を算出することができます。 \begin{gather} \hat{\beta}-\mathrm{S.E.} \left(\hat{\beta}\right) \cdot Z_{0.5\alpha} \le \beta \le \hat{\beta}+\mathrm{S.E.} \left(\hat{\beta}\right) \cdot Z_{0.5\alpha} \end{gather} さらに、ロジスティック回帰係数と調整オッズ比の関係から、以下のように、信頼区間を算出することができます。 \begin{gather} e^{\hat{\beta}-\mathrm{S.E.} \left(\hat{\beta}\right) \cdot Z_{0.5\alpha}} \le \mathrm{OR} \le e^{\hat{\beta}+\mathrm{S.E.} \left(\hat{\beta}\right) \cdot Z_{0.5\alpha}} \end{gather}
ロジスティック回帰分析をする際の注意点
説明変数の数とサンプルサイズのバランス
回帰分析の妥当性は、誤差が少なく、信頼のおけるデータを用いることはもちろん、モデルに投入する要因の数に影響を受けます。ロジスティック回帰分析では、共変量1個につき、10~15倍のアウトカムの発生数が必要とされ、発生数が足りないと結果の信頼性が下がるとされています。そのため、線形回帰分析と同様、やみくもに説明変数を投入することは適切ではありません。ここで注意すべきは、必要なデータ数は、「観測数」ではなく、アウトカムの発生数である点です。例えば、1年問で70例のイベントしか観察できないと予想される場合、モデルに入れられる変数の数は、7から10個となります。
多重共線性
他の回帰分析全般と同様、ロジスティック回帰モデルを用いる場合も、多重共線性の問題への配慮が必要です。つまり、共変量間に強い相関があったり、一次従属な変数関係があったりする場合には、解析が不可能であったり、たとえ結果が求められたとしてもその信頼性は低くなったりするという問題があります。例えば、BMと体重が同じ回帰式にあった場合、正しい結果が導き出せません。これは、BMIの計算式に体重が入っているためで、このような場合に体重とBMIは一次従属な変数関係にあると表現し、多重共線性が認められます。共変量間で相関関係をチェックし、相関係数が0.8もしくは0.9を越えるような場合には、多重共線性を疑う必要があり、その場合には、“どちらかいっぽう”を共変量に採用します。
要因効果の等間隔性
モデルに投入する要因、特に年齢などの連続変数の場合、どの年齢層でもアウトカムに対して同じ程度の効果があることを仮定しています。つまり、40 歳であっても80 歳であっても、10 歳年齢が上がったときのアウトカムの変化が等しいと仮定しています。もしこれを満たさないと考えられるなら、年齢をカテゴリー化するなどの対応が必要となります。
交互作用の影響
回帰モデルに投入した要因は、すべてお互いに影響がないという仮定があります。例えば、死亡をアウトカムとした回帰分析に「年齢」と「重症度」を投入している場合、「重症度」が死亡に与える影響は、若年者であっても高齢者であっても同じであると仮定していることになります。若年者と高齢者で重症度が死亡に与える影響が異なると考えられる場合は、年齢と重症度の交互作用項(回帰式では年齢×重症度という変数)をモデルに入れる必要があります。
対応のあるデータ・マッチング研究
個別マッチングを行ったケース・コントロール研究など(すなわち、「対応のあるデータ」である場合)で、ロジスティック回帰モデルを用いた交絡の調整を行う場合、マッチングをしない場合に用いられる通常の最尤法ではなく、条件つき最尤法によって、回帰係数を推定する必要があります。そのため、多くの統計ソフトウェアにおいては、「対応のあるデータ」用の条件つき最尤法と「対応のないデータ」用の無条件最尤法の2つの方法を選択することができます。対応の有無は、ある程度の相関があるか否かによって判断されますが、データの構造上、対応のある・なしの判断に迷う場合は、対応のあるデータとして、条件つき最尤法を用いた方が良い$^\mathrm{(5)}$とされています。
参考文献
- ダグラス・アルトマン 著, 木船 義久, 佐久間 昭 訳. 医学研究における実用統計学. サイエンティスト社, 1999, p.284-289
- 浜田 知久馬 著. 学会・論文発表のための統計学:統計パッケージを誤用しないために. 真興交易医書出版部, 2012, p.173-208
- ケネス・ロスマン 著, 矢野 栄二, 橋本 英樹, 大脇 和浩 監訳. ロスマンの疫学:科学的思考への誘い. 篠原出版新社, 2013, p.295-323
- 丹後 俊郎, 山岡 和枝, 高木 晴良 著. ロジスティック回帰分析:SASを利用した統計解析の実際. 新版, 朝倉書店, 2013, p.1-8
- Cornfield, J.. Joint dependence of risk of coronary heart disease on serum cholesterol and systolic blood pressure: a discriminant function analysis. Fed Proc. 1962, 21(4), p.58-61.
- Walker, S.H. & Duncan, D.B.. Estimation of the probability of an event as a function of several independent variables. Biometrika. 1967, 54(1), p.167-179.
- Hall, G.H. & Round, A.P.. Logistic regression-explanation and use. J R Coll Physicians Lond. 1994, 28(3), p.242-246, PMCID: PMC5400976
- Bender, R. & Grouven, U.. Ordinal logistic regression in medical research. J R Coll Physicians Lond. 1997, 31(5), p.546-551, PMCID: PMC5420958
- 福田 治久. 疫学・統計解析シリーズ: 多変量回帰分析. 日本環境感染学会誌. 2014, 29(4), p.240-255, doi: 10.4058/jsei.29.240
- 五十嵐 中. わかりませんから始める医療統計: (15)値のズレは、誰のせい?:重回帰とロジスティック回帰. 調剤と情報. 2015, 21(3), p.353-359.
引用文献
- ケネス・ロスマン 著, 矢野 栄二, 橋本 英樹, 大脇 和浩 監訳. ロスマンの疫学:科学的思考への誘い. 篠原出版新社, 2013, p.296-297
- ケネス・ロスマン 著, 矢野 栄二, 橋本 英樹, 大脇 和浩 監訳. ロスマンの疫学:科学的思考への誘い. 篠原出版新社, 2013, p.303
- Truett, J., Cornfield, J. & Kannel, W.. A multivariate analysis of the risk of coronary heart disease in Framingham. J Chronic Dis. 1967, 20(7), p.511-524, doi: 10.1016/0021-9681(67)90082-3
- 浜田 知久馬 著. 学会・論文発表のための統計学:統計パッケージを誤用しないために. 真興交易医書出版部, 2012, p.194-199
- 福田 治久. 疫学・統計解析シリーズ: 多変量回帰分析. 日本環境感染学会誌. 2014, 29(4), p.240-255, doi: 10.4058/jsei.29.240
脚注
- そのほか、単回帰や重回帰で前提とされている、誤差が正規分布に従うという前提も多くの場合で、満たされないことが想定される点も問題となります。
- もちろん、実際には多くの場合が比例尺度、すなわち「負の値は取らない変数」ですが、数学的には間隔尺度である場合も考慮し、最も一般的なかたちを考えるため、すべての実数と取り得るものとしてモデルを考えます。



0 件のコメント:
コメントを投稿