因果関係の推論にあたっては、選択バイアスと情報バイアス以外に、交絡が大きな問題となるため、交絡の発生を予防したり、その影響を取り除いたりすることは非常に重要です。本稿では、交絡の意味や原因、対処方法の概要などを紹介しています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
交絡とは?
交絡 confounding とは、ある危険因子とアウトカムの関係を評価する際、第3の因子の影響によって、見かけ上、関連があるように(もしくは、ないように)見えてしまう現象のことです。
例えば、ライターの所持状況と肺がんの発症の関連についてケース・コントロール研究で調べた結果、次のようなデータが得られたとします$^\mathrm{(1)}$。
| ライター所持 $ \left(E\right)$ | ライター非所持 $(\bar{E})$ | 合計 | |
|---|---|---|---|
| ケース群 $ \left(D\right)$ | $66$ | $34$ | $100$ |
| コントロール群 $(\bar{D})$ | $34$ | $66$ | $100$ |
このとき、曝露オッズ比は、 \begin{align} \mathrm{\widehat{OR}}=\frac{66\times66}{34\times34}=3.8 \end{align} となり、 ライターを持っていると、肺がんにかかりやすくなることが分かりました。
これは分かりやすい例ですが、もちろん、ライターを持っていること自体が肺がんの原因となるわけはありません。では、なぜこれら2つに関連があるように見えたのかといえば、それは、ライターの所持と肺がんは、どちらも「喫煙」という第3の因子に関連があったからです。先ほどの結果を、喫煙の有無で更に分けると、次のようになりました。
| ライター所持 $ \left(E\right)$ | ライター非所持 $(\bar{E})$ | 合計 | |
|---|---|---|---|
| ケース群 $ \left(D\right)$ | $63$ | $7$ | $70$ |
| コントロール群 $(\bar{D})$ | $27$ | $3$ | $30$ |
| ライター所持 $ \left(E\right)$ | ライター非所持 $(\bar{E})$ | 合計 | |
|---|---|---|---|
| ケース群 $ \left(D\right)$ | $3$ | $27$ | $30$ |
| コントロール群 $(\bar{D})$ | $7$ | $63$ | $70$ |
このとき、それぞれの曝露オッズ比は、 \begin{gather} \mathrm{{\widehat{OR}}_S}=\frac{63\times3}{27\times7}=1.0\\ \mathrm{{\widehat{OR}}_{NS}}=\frac{3\times63}{7\times27}=1.0 \end{gather} したがって、どちらの群でもライター所持と肺がんは関係ないことが分かりました。このように、曝露と疾病発生の関係の観察に影響を与え、真の関係とは異なった観察結果をもたらす第3の因子のことを交絡因子 confounding factors, confounders といいます。
この例の場合、以下のように、ライター所持と喫煙に関連があり、また、喫煙が肺がんの危険因子であるため、あたかもライター所持が肺がんのリスクを上昇させているようにみえたということです。
| 喫煙あり $ \left(E\right)$ | 喫煙なし $(\bar{E})$ | 合計 | |
|---|---|---|---|
| ケース群 $ \left(D\right)$ | $70$ | $30$ | $30$ |
| コントロール群 $(\bar{D})$ | $30$ | $70$ | $70$ |
喫煙の曝露オッズ比は、 \begin{gather} \mathrm{\widehat{OR}}=\frac{70\times70}{30\times30}=5.4 \end{gather}
| 喫煙あり $ \left(E\right)$ | 喫煙なし $(\bar{E})$ | 合計 | |
|---|---|---|---|
| ライター所持 $ \left(D\right)$ | $90$ | $10$ | $30$ |
| ライター非所持 $(\bar{D})$ | $10$ | $90$ | $70$ |
喫煙の曝露オッズ比は、 \begin{gather} \mathrm{\widehat{OR}}=\frac{90\times90}{10\times10}=81 \end{gather}
交絡はなぜ起きるのか
交絡が起こるためには、①ある因子が交絡因子となるための条件を満たし、かつ、②交絡因子の分布が比較する群間で異なる必要があります。
交絡因子の3要件
ある因子が曝露と疾病発生の関連において交絡因子として作用するためには、次の3つの要件が必要となります。
- アウトカムの発生に影響を与えている(危険因子である)
- 曝露因子(影響を調べている因子)と関連がある
- 曝露因子(影響を調べている因子)とアウトカムの中間因子ではない
このうちの1つでも欠けると交絡因子とはなりませんが、疫学研究では性と年齢は必ず交絡因子として取り扱われます。これらの関係は次の図のように表すことができます。この中で、因子Aは、影響を調べている因子で、「表に見えている因子」です。いっぽう、因子Bは、通常は、その存在に初めから気づいていることは少なく、落とし穴のように「裏に隠れている第3の因子」と考えてください。

このうち、パターンA、B、Cは上記の3要件を満たしているため、因子Bは交絡因子となります。
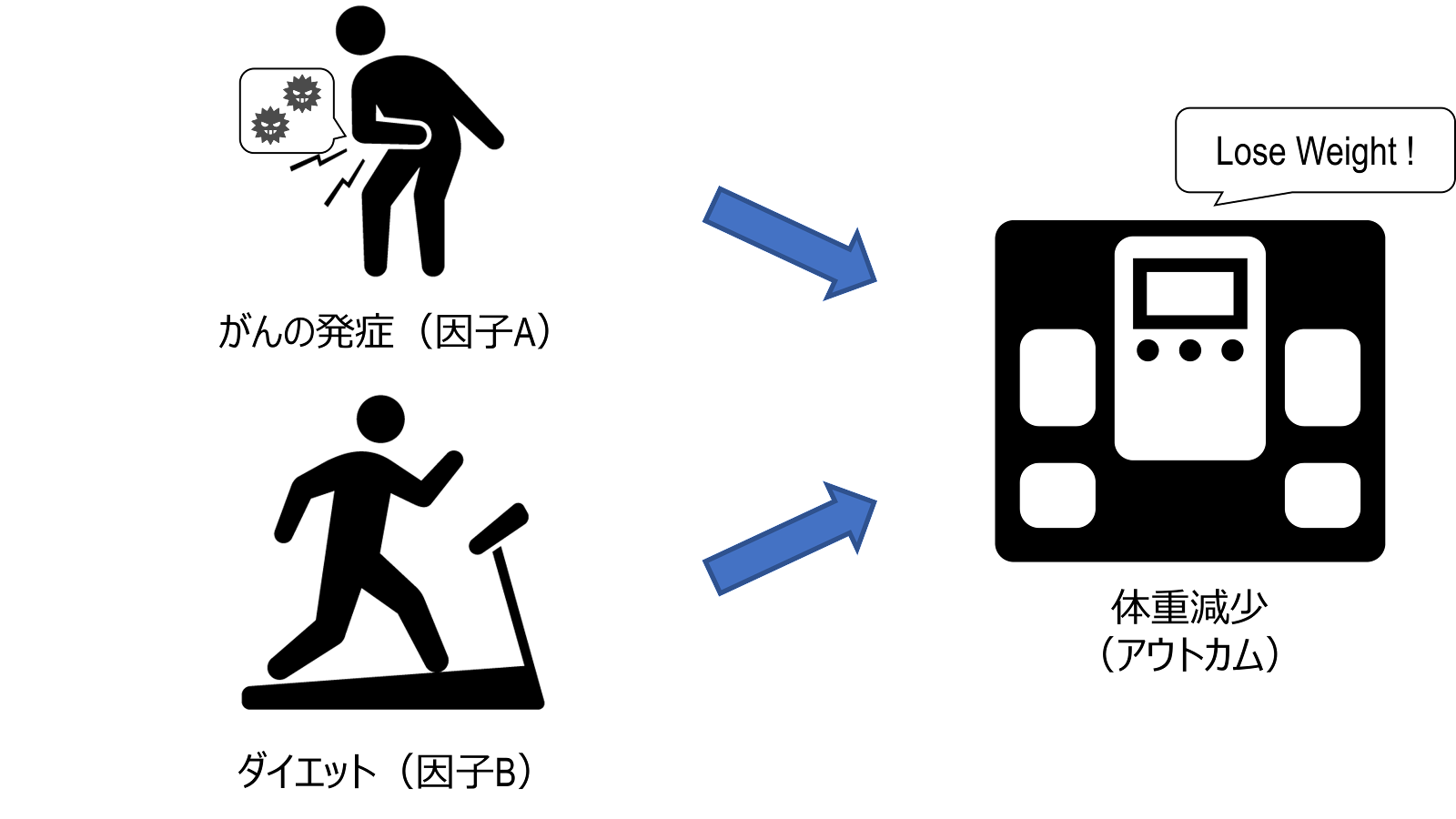
いっぽう、パターンD、E、F、Gは交絡因子となりません。パターンDは、因子Aと因子Bの間に関連がないので、条件を満たしません。ただし、「体重の減少」(アウトカム)と「がんの発症」(因子A)と「ダイエット」(因子B)の関係のように、「共通効果への限定」というバイアスが生じる可能性はあります。
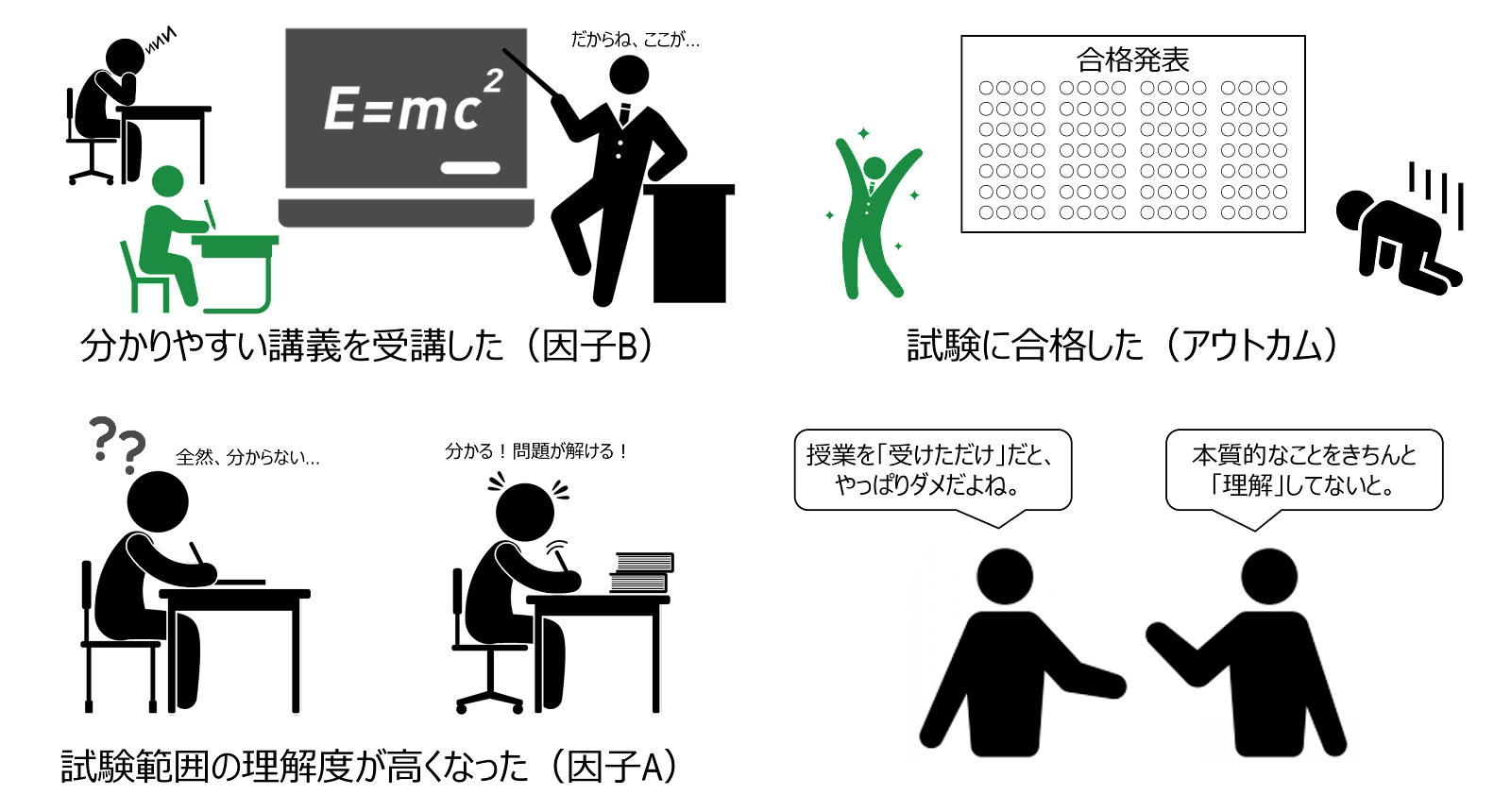
パターンEは、因子Bがアウトカムの発生に関与していないので、条件を満たしません。例えば、「分かりやすいと評判の講師の講義を受講した」(因子B)、「試験範囲の理解度が高くなった」(因子A)、「試験に合格した」(アウトカム)という関係がこの関係に当てはまります。
パターンFもEと同様に、因子Bがアウトカムの発生に関与していないので、条件を満たしません。例えば、「喫煙する」(因子A)、「コーヒーを飲む」(因子B)、「肺がんになる」(アウトカム)という関係がこの関係に当てはまります。この場合、因子Bについては、観察の対象としておらず、存在に気づかずとも、問題ありませんが、因子Aと因子Bを入れ替えると交絡因子(パターンA)となり、「コーヒーの摂取」が「肺がん」を引き起こしているかのように見えます。

中間因子と交絡因子
パターンGは、因子Bが中間因子であるため交絡因子になりません。中間因子 mediator とは、「要因Aが原因となり、要因Bが発生し、要因Bによってアウトカムが発生する」という因果関係の連鎖の中で、中間での橋渡しの役となる因子のことで、介在因子 intervening factor とも呼ばれます。
例えば、先の例において、「分かりやすいと評判の講師の講義を受講した」(因子A)、「試験範囲の理解度が高くなった」(因子B)、「試験に合格した」(アウトカム)という関係を考えたときがこの関係に当てはまると思われます。いいかえれば、因子Bはアウトカムの発生の「直接的な原因」、因子Aは、「間接的な原因(遠因)」ともいえます。
その因子が交絡因子となるか中間因子となるかは、状況によります。例えば、「Youtubeの銀の盾を持っている」(因子C)、「試験範囲の理解度が高くなった」(因子B)、「試験に合格した」(アウトカム)という関係を考えたとき、因子Bは、因子Cとアウトカムの関係における交絡因子になります。この場合は、「試験範囲の理解度が高い」からこそ、「分かりやすい動画を作ることができるようになり、チャンネル登録者が増えて、銀の盾を手に入れた」、あるいは「試験に合格した」という因果関係で、「銀の盾を持っているから試験に合格した」、「試験に合格したから銀の盾を持っている」というわけではありません。

中間因子と交絡因子の区別は重要で、交絡因子の調整は、因果関係を明らかにするうえで役立ちますが、中間因子で調整すると、因果関係自体が見えなくなってしまうので、注意が必要です。
群間での分布の不均等
ただ、ある因子が交絡因子となる条件を満たしていても、必ず交絡が発生するわけではありません。交絡が発生するには、疾病発生の予測因子が曝露状況の区分間で不均衡な分布をしている必要があります。例えば、年齢は多くの病気の危険因子とされていますが、曝露群と非曝露群で年齢分布が異ならなければ、年齢はどちらでも同程度の影響しか及ぼさないため、交絡因子とならず、結果が歪められることはありません。いっぽう、ライターと肺がんの例のように、ライターの所持状況によって喫煙確率が異なる場合、交絡が発生します。
このように性質の異なるグループ間での比較を英語で“compare apples and oranges"(リンゴとミカンを比べる)といいます。リンゴとミカンは性質が異なるためフェアな比較はできないという意味です。
交絡によるバイアスの方向(シンプソンのパラドックス)
交絡は、効果を過大評価する方向と過小評価する方向のどちらにもバイアスを生じさせるため、注意が必要となります。
効果の過大評価(見かけ上、関連が生じる)
例えば、ある薬剤の効果を調べるために、曝露群(実薬群)と非曝露群(偽薬群)をそれぞれ100人ずつ用意し、薬剤が有効か無効かを判定したとします。その結果、次の表が得られました$^\mathrm{(2)}$。
| 有効 $ \left(E\right)$ | 無効 $(\bar{E})$ | 合計 | |
|---|---|---|---|
| 曝露群 $ \left(D\right)$ | $71$ | $29$ | $100$ |
| 非曝露群 $(\bar{D})$ | $52$ | $48$ | $100$ |
各群の有効割合は、 \begin{gather} \pi_1=71\% \quad \pi_0=29\% \end{gather}
ここでは、例えば鎮痛薬の臨床研究を想定して、痛みの改善を評価しているものとします。痛みの改善なので、かなりのプラセボ効果があると予想されます。全体では非曝露群の有効割合52%に対し、曝露群では71%と、薬剤投与によって有効割合が増加する傾向が見られますが、これは交絡因子による見かけ上の関連によって生じた可能性があります。
| 有効 $ \left(E\right)$ | 無効 $(\bar{E})$ | 合計 | |
|---|---|---|---|
| 曝露群 $ \left(D\right)$ | $63$ | $7$ | $70$ |
| 非曝露群 $(\bar{D})$ | $36$ | $4$ | $40$ |
各群の有効割合は、 \begin{gather} \pi_{H1}=90\% \quad \pi_{H0}=90\% \end{gather}
| 有効 $ \left(E\right)$ | 無効 $(\bar{E})$ | 合計 | |
|---|---|---|---|
| 曝露群 $ \left(D\right)$ | $8$ | $16$ | $30$ |
| 非曝露群 $(\bar{D})$ | $22$ | $44$ | $60$ |
各群の有効割合は、 \begin{gather} \pi_{L1}=27\% \quad \pi_{L0}=27\% \end{gather}
2つの層を一緒にすると、曝露群と非曝露群の間で有効割合に19%の差があります。しかし、軽症の層では27%と27%。重症では90%と90%で2つの層とも差がありません。どうしてこのようなことが起きたのでしょうか?
軽症では有効割合27%に対し、重症では90%と重症の方が、圧倒的に有効割合が高い傾向にある、すなわち、元々痛みの強い患者の方が、痛みが改善しやすい傾向にあり、「疾患の重症度」は有効割合に決定的な影響を与える因子と考えられます。重症度は反応変数である痛みの改善と関連するので、交絡因子であるための1つ目の条件を満たします。もし、薬剤の投与とも関連していれば、2つ目の条件も満たし、交絡が起きることになります。
曝露群と非曝露群で重症度の分布を比較すると、曝露群では重症70%、軽症30%に対して、非曝露群では40%と60%で、曝露群では重症の患者が多くなっていました。重症度は薬剤投与とも関連する因子となっています。重症度を無視したときの曝露群と非曝露群の差は、曝露群では重症の患者が多く、さらに飛症な患者の方が、痛みが改善しやすい傾向にあっために生じた見かけ上の差となります。
効果の過少評価(見かけ上、関連が消滅する)
逆に次のように、交絡因子の影響によって関連が隠されてしまう場合もあります$^\mathrm{(2)}$。
| 有効 $ \left(E\right)$ | 無効 $(\bar{E})$ | 合計 | |
|---|---|---|---|
| 曝露群 $ \left(D\right)$ | $140$ | $60$ | $200$ |
| 非曝露群 $(\bar{D})$ | $140$ | $60$ | $200$ |
各群の有効割合は、 \begin{gather} \pi_1=70\% \quad \pi_0=70\% \end{gather}
| 有効 $ \left(E\right)$ | 無効 $(\bar{E})$ | 合計 | |
|---|---|---|---|
| 曝露群 $ \left(D\right)$ | $72$ | $8$ | $80$ |
| 非曝露群 $(\bar{D})$ | $112$ | $28$ | $140$ |
各群の有効割合は、 \begin{gather} \pi_{H1}=90\% \quad \pi_{H0}=80\% \end{gather}
| 有効 $ \left(E\right)$ | 無効 $(\bar{E})$ | 合計 | |
|---|---|---|---|
| 曝露群 $ \left(D\right)$ | $68$ | $52$ | $120$ |
| 非曝露群 $(\bar{D})$ | $28$ | $32$ | $60$ |
各群の有効割合は、 \begin{gather} \pi_{L1}=57\% \quad \pi_{L0}=47\% \end{gather}
全体では非曝露群の有効割合70%に対し、曝露群でも70%と、全く差がありません。ところが、軽症の層では47%と57%、重症では80%と90%で、2つの層とも薬剤による10%の上乗せ効果があります。
これらの例のような、「全体としてみたときの結論と層別してみたときの結論が異なる現象」は、シンプソンのパラドックス Simpson's paradox として知られています。
適用による交絡
薬剤の効果に関する研究では、介入(薬剤投与の割り付け)を行わない非実験的研究デザイン(観察研究)を用いることがよくありますが、このような観察研究で薬剤服用者と非服用者の結果を比較する際には、特に注意すべき点があります。それは、「治療はほとんどの場合悪いアウトカムに対するリスクが高い患者に適応されることが多い」という点です。
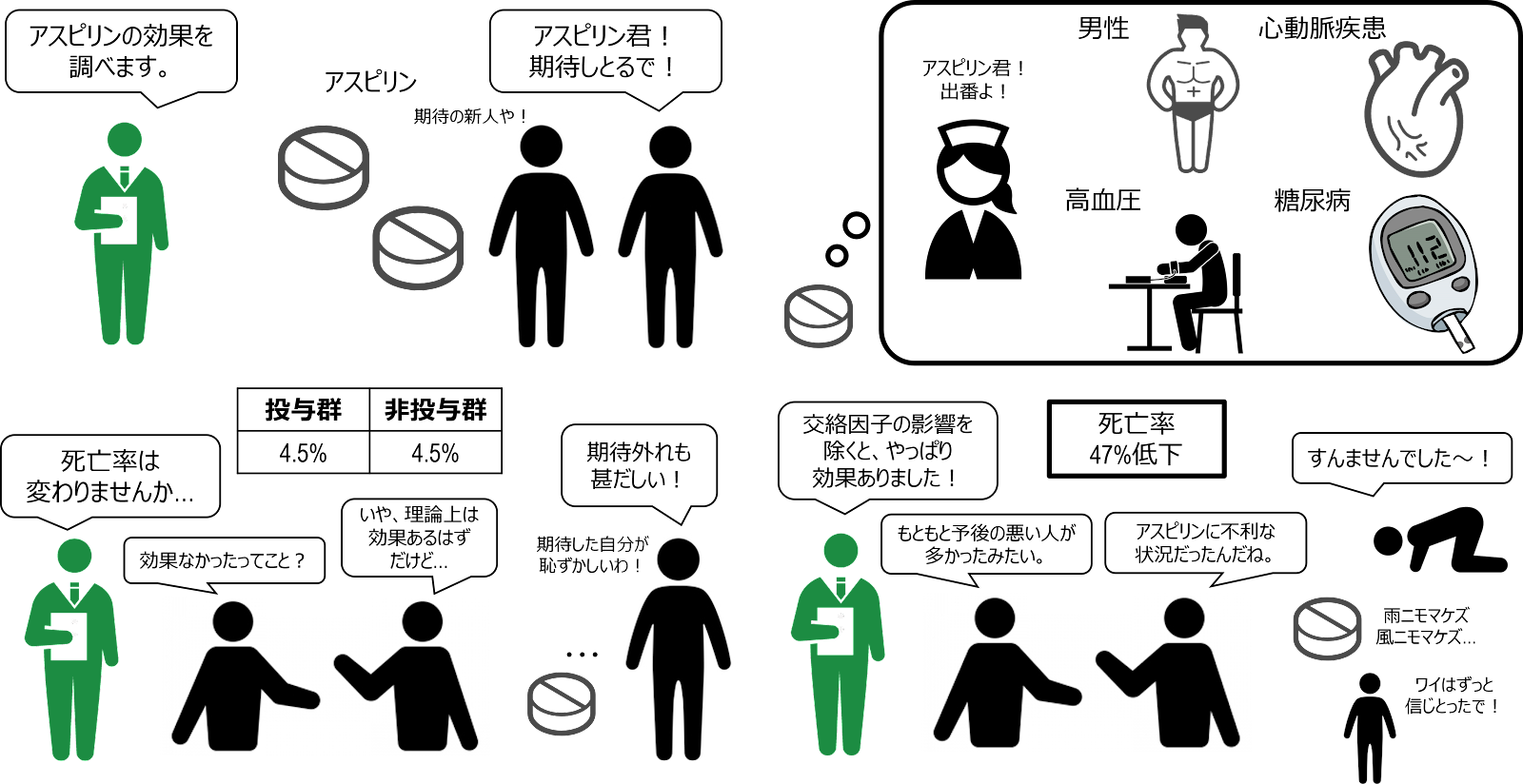
例えば、アスピリンの効果に関する研究$^\mathrm{(3)}$では、心臓病が理由でエコーをとった6174名の患者の3年間の生存率をアスピリン使用群と非使用群で比べました。その結果、死亡率は両群ともに4.5%で違いは検出されませんでした(P=0.5)。このデータをもとに、「アスピリンによる延命効果はなし」と判断できるかというと、そうとは限りません。
それは、背景因子が両群で異なっていたからです。この研究にどのような人が参加したか、患者背景を見てみると、アスピリン使用者は非使用者に比べて、平均年齢が6歳上で、男性、糖尿病、高血圧の割合が多く、特に心動脈疾患の割合は使用群70%に対し、非使用群20%とアスピリンを使っていない人は使った人より、かなり心臓病リスクが低いことが分かりました。つまり、「リスクが低いから、アスピリンをあまり使わなかった」ということです。
つまり、アスピリン使用の有無にかかわらず、もともとアスピリン使用群には、非使用群に比べて、すでに予後の悪い患者が多く入っているので、「効果がなかったのは、アスピリンが効かなかったから」という解釈の他に、「最初から予後の良くない人が多く入っていたのでアスピリンが効いたにもかかわらず、生存率に差が出なかった」という解釈も可能となります。実際、後述するような手法で交絡の影響を取り除くと、服用者における死亡率は、非服用者よりも47%小さいという結果になりました(P=0.002)。
こうした種類の交絡、すなわち、有益な因子の効果がアウトカムの原因となる因子との関連によって打ち消されてしまうというタイプの交絡のことを、抑制効果 suppression といい、そうした因子を抑制因子 suppressor といいます。この種の交絡は、治療効果の観察的研究でしばしば遭遇する問題で、治療の有効な効果が打ち消されるばかりか、有害にさえ見えたりすることを適応による交絡 confounding by indication といいます。
交絡因子の制御方法の概要
選択バイアスと情報バイアスは、必ず研究計画の段階で対処しなければならないバイアスでしたが、交絡は、研究計画の段階でだけでなく、解析段階でもある程度までその影響を排除することも可能です。
観察的研究で、どこまで交絡に対処できるかは、研究者がいかに交絡する可能性のある因子を測定できるかにかかっています。交絡に対処するには、まず、予測因子と関連があり、かつアウトカムの原因となる可能性のある因子(例:年齢や性別)をリストアップします。そして、次に、どの段階で対処するか、つまり、研究デザインの段階か、あるいはデータ解析の段階かを決定します。
具体的な方法としては、研究計画段階で「無作為化」、「対象者の限定」、「マッチング」の3 通り、解析段階で「層別解析」、「数学的モデリング(多変量解析)」の2 通りがあります。本稿では、これらの方法の概要を紹介し、より詳細な内容については、別稿で解説したいと思います。
研究計画段階での対処法①:無作為化
無作為化 randomization 、あるいは無作為割付 random allocation とは、コインの表が出れば「介入あり」、裏が出れば「介入なし」のように、対象者が介入治療を受けるかそうでないかの割り付けを完全に無作為に行うことによって、両群間のさまざまな因子の分布をそろえようとする手法のことです。無作為化は、研究実施者が曝露と非曝露を決めることができる介入研究や実験研究などの場合のみ用いることが可能で、観察研究の場合は、用いることができません。
無作為化は、観察研究では用いることのできない手法ですが、極めて有効性の高い交絡因子の制御法とされています。それは、無作為化によって、すべての因子が介入群・非介入群で均等に分布することが期待できるからです(つまり、交絡因子の分布が群間で異なるという、交絡の発生原因を解消してくれます)。この点、他の方法では既知の交絡因子しか制御できませんが、無作為化の場合は、交絡因子として作用するかどうか、あるいは、その存在に気づいているか否か(既知・未知を問わず)にかかわらず、(ある意味で自動的に)揃ってくれると期待できる点が、有用であるとされています。このため、理論的には「結果の違いは介入の効果である」という解釈をしやすくなり、また、要因のランダム化によって、Fisher 検定に代表されるランダム化に基づく統計解析の基礎も与えられます。
ただ、無作為化は、交絡が起こらないことを保証するものではなく、偶然によって交絡を引き起こす不均等が生じることもあります。こうした点への対策としては、サンプルサイズをなるべく大きくして、不均衡が発生する確率を小さくしたり、解析段階での方法と組み合わせて、交絡の影響を取り除くなどの方法があります。
研究計画段階での対処法②:対象者の限定
対象者の限定 specification, restriction とは、対象者を交絡因子の1つの要因をもつ者のみに制限する手法で、観察研究か介入研究かにかかわらず、どんな研究にも適用できる手法です。例えば、ライター所持と肺がんの関係において、観察対象者を喫煙者のみ、あるいは非喫煙者のみとすると、喫煙習慣が交絡因子として作用する余地はなくなり、それでもなお、ライター所持と肺がんの間に関連があれば、それは喫煙の影響によるものではないことになります。
対象者の限定は、選択した因子の交絡を確実に防止することができますが、無作為化とは異なり、未知の交絡因子は制御できません。
また、多くの交絡因子について同時に用いたり、あるいは交絡因子の幅を狭く設定しすぎると、十分なサンプルサイズを確保できなくなるという問題が生じます。
さらに、対象者の限定は、単純で容易な方法であり、解釈も簡単ですが、たとえば喫煙者のみで得られた結果を非喫煙者にもそのまま適用してよいか、という点で問題が残ります。コーヒーと心筋梗塞の関係を調べたいとき、もしかしたら、非喫煙者ではコーヒーが心筋梗塞の原因になっていなくても、喫煙者ではコーヒーが心筋梗塞の原因になっているかも知れません$^\mathrm{(i)}$。つまり、対象者を限定することによって、その研究から得られる情報の一般化可能性(外的妥当性)が限定される危険があり、この例で言えば、得られた結果を喫煙者にあてはめることはできないことになります。
研究計画段階での対処法③:マッチング
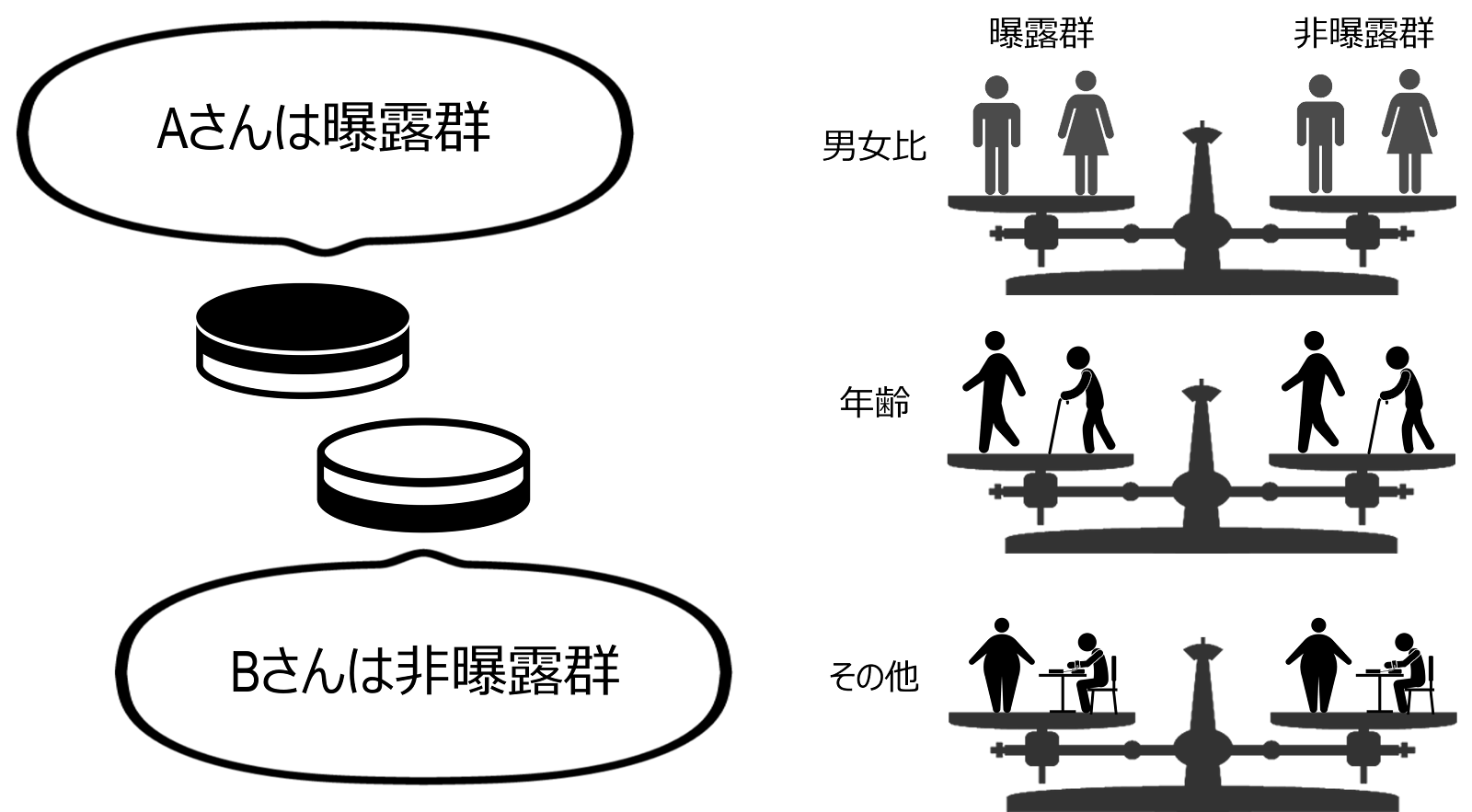
マッチング matching は、比較する群同士で交絡因子のレベルが等しくなるようにサンプリングする方法です。例えば、喫煙者のケース群を1人選ぶとき、その人に対応させて喫煙者のコントロール群を選んでペアを作るという作業がマッチングに当たります。すなわち、介入研究における無作為化で、交絡因子を2つの群で均等に分布させることを、観察研究において人為的に行っているものといえます。これによって、予測因子とアウトカムの関連に対するそれらの因子の影響を完全に除去することができ、限定よりも結果の外的妥当性が高いため、よく用いられる方法となっています。マッチングは、コホート研究、ケース・コントロール研究のどちらでも行うことができますが、特にケース・コントロール研究でよく用いられる方法です。
ただし、マッチングには、①マッチングした因子の影響は分からなくなる、②多くの交絡因子でマッチしようとするとマッチさせる相手が見つからないことがある、③マッチした因子に関して対象者の脱落状況が群間で異なると、せっかくのバランスが崩れてしまう、④ケース・コントロール研究では、マッチングが新たな選択バイアスの原因となることがある、などの欠点もあります。
解析段階での対処法①:層別解析
層別解析 stratified analysis、または、層化 stratification とは、比較する群間の交絡因子のレベルを揃えて比較する解析上の手法で、対象者を交絡因子のレペル(層 strata)に応じてサブグループ化し、各層ごとに予測因子とアウトカムの関連を検討します。ライターと肺がんの例において、全体を喫煙者と非喫煙者に分けて、それぞれの層で曝露オッズ比を求めたことが、層別解析にあたります。また、標準化やマンテル・ヘンツェルの方法など、層ごとに観察した結果を統合することによって、全体の傾向を観察する方法もあります。
層別解析は、次の数学的モデリングと比較して、数学的な仮定も少ないため、単純で分かりやすく、結果の解釈が容易という長所があります。そのいっぽう、多くの交絡因子で層別すると、層内の対象者数が少なくなったり、時には比較する一方の群に対象者が存在しないといったことが生じることもあります。そのため、結果が不安定になる(信頼区間が広くなる)、あるいは効果自体の推定ができなくなるという短所もあります。
解析段階での対処法②:数学的モデリング
数学的モデリング mathematical modeling は、多変量解析 multivariate analysis を用いて相互に関連する因子(例えば、年齢、性別、人種など)を同時に制御する手法です。通常は重回帰分析、ロジスティック回帰分析(コホート研究、ケース・コントロール研究)、ポアソン回帰分析(主にコホート研究)、Coxの比例ハザード回帰分析(コホート研究や介入研究)が用いられます。
多変量解析による調整の大きな利点は、多数の因子を同時に制御できることや変数が連続変数のとき(カテゴリーに分割することなく)、そのまま扱うことができることです。また、交互作用項を用いて、変数間の交互作用(効果修飾)の有無を検討できることも利点として挙げられます。
ただ、多変量解析には欠点もあります。最も重要な欠点は、モデルが常にあてはまるとは限らないことです。最近、統計解析ソフトが簡単に利用できるようになってきましたが、自分の研究データにその統計学的モデルが本当にあてはまるのかどうかをよく考えずに用いると、正しい結果が得られないことがあります。
第2の欠点は、その解析結果の理解が容易ではないということです。これは、複雑な項や交互作用項を用いる場合には特に問題となります。
実際の交絡制御
実際の研究で交絡を制御する際には、計画の段階で3種類のうちの1つか2つの方法を取り入れ、なおかつ解析の段階で層化か多変量解析のどちらかを用いてだめ押ししていることが多いといえます。それは、計画上の工夫だけでは交絡を完全に防ぐことは難しいことが多く、データ解析の段階で、当初想定していなかった因子が交絡因子となり得ることが分かる可能性があるからです。
研究デザイン段階の方法では、どの因子を交絡因子として扱うかを、研究の開始時点で決めておく必要があり、いったん決めたら、その因子とアウトカムの関連を検討することはできません。これに対し、データ解析段階の対策では、そうした決定を、データを解析する段階で行えばよく、どの因子を交絡因子として扱うかは、データを見ながら判断することができます。
対象者の限定は、あまり意識されませんが、多少なりとも対象者の年齢を限定していることが多く、観察を一方の性に限定した研究も多しため、実質的にはほとんどの研究で用いられています。
また、介入研究ではCONSORT声明などのガイドラインの影響により、無作為化が不可欠となっているほか、ケース・コントロール研究では、性別と年齢をマッチさせることがよくあります。
近年、統計ソフトの普及などの影響で多変量解析を用いることが一般的になっています。特に、ケース・コントロール研究では、単変量解析でもロジスティック・モデルを用いて結果を求めることも増えています。ただ、複数の変数をモデルに組み込む多変量解析では、モデルの設定などややこしい問題も多く、自分が用いようとする統計解析の回帰係数などの高度な統計量について、その意味を自分で説明できるようになっていることが望ましいとされています。したがって、いきなり高度な解析を行うよりも、まずは、単純な層化分析を行い、その結果とより高度な統計解析の結果との間にかなり大きな違いが見られる場合には、統計家に相談するといった手順をとることが望まれています。
参考文献
- 浜田 知久馬 著. 学会・論文発表のための統計学:統計パッケージを誤用しないために 新版. 真興交易医書出版部, 2012, p.159-161
- ケネス・ロスマン 著, 矢野 栄二, 橋本 英樹, 大脇 和浩 監訳. ロスマンの疫学. 篠原出版新社, 2013, p.193-206
- スティーブン・ハリー, スティーブン・カミングス ほか 著, 木原 雅子, 木原 正博 訳. 医学的研究のデザイン. メディカル・サイエンス・インターナショナル, 2014, p.141-150
- 中村 好一 著. 基礎から学ぶ楽しい疫学. 医学書院, 2020, p.104-113
引用文献
- 中村 好一 著. 基礎から学ぶ楽しい疫学. 医学書院, 2020, p.105
- 浜田 知久馬 著. 学会・論文発表のための統計学:統計パッケージを誤用しないために 新版. 真興交易医書出版部, 2012, p.159-161
- Gum, P.A., Thamilarasan, M., Watanabe, J. et al.. Aspirin use and all-cause mortality among patients being evaluated for known or suspected coronary artery disease: A propensity analysis. Journal of the American Medical Association. 2001;286(10):1187-1194, doi: 10.1001/jama.286.10.1187
脚注
- コーヒーの心筋梗塞に対する影響が喫煙者と非喫煙者で異なるこのような現象を、効果修飾 effect modification、あるいは交互作用 interaction といいます。



0 件のコメント:
コメントを投稿