医学や薬学などの分野では、長らく治療効果の優越性を示すための試験・研究が中核を担ってきましたが、近年、安全性や費用などの面で優位性がある手法に関する同等性・非劣性試験に注目が集まっています。本稿では、そうした同等性・非劣性試験の概要と同等性・非劣性を示すうえでのポイントについて解説しています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
同等性試験の登場
医学や薬学は、基本的に「より良い治療法」の開発を目的としています。すなわち、「従来の方法よりも病気の治癒率が高い治療法」や「既存の薬よりも長く生きられる薬」を生み出すことに主眼を置き、それを立証するために無作為化比較試験などの臨床試験を実施するということです。このように、新しい方法の治療効果が従来の方法よりも優れていることを示す目的で行われる研究を優越性試験 superiority trial と呼びます。
しかし近年、必ずしも治療効果の高さだけを絶対視しない考え方が現れています。たしかに我々にとって、治療効果の高さは最も関心のあるポイントですが、いっぽうでその治療を受けるための費用が膨大で手が出せなかったり、世界に数人しかその手術をできる人がいないということになってしまうと、その治療法にアクセスできる人が限られてしまい、結果として「救える人の数」を最大化することができなくなってしまいます。
こうした意味で、「治療効果の高さ」はその治療の「有用性」を決める要素のうちのひとつであるとも考えることができます。この点、「安全性の高さ」、「価格の安さ」、「副作用や合併症の少なさ」、「侵襲性・毒性の低さ」、「投与・適用の簡便さ」などの観点では従来の方法よりも優れており、かつ、「治療効果の高さ」という観点では、「優れるわけではないけど同じくらいの効果を発揮する」という方法が提供できるのであれば、それはそれで世に広めてもいいと言えるでしょう。こうした背景から生まれたのが、同等性試験 equivalence trial と呼ばれる研究デザインです。
同等性の示し方①:「有意差なし」は「同等である」ではない
「同じくらいの治療効果がある」、すなわち、治療効果の「同等性」が示せればよいということになりましたが、では、どうやって「同等性」を示せばよいのかが問題となります。この点、既存の仮説検定≒優越性試験の枠組みでは、「治療法AとBの治癒確率には差がある」、もしくは「治療法Aの治癒確率はBよりも高い」という仮説を示すために、「治療法AとBの治癒確率には差がない」という帰無仮説を考え、実際に得られたデータをもとに帰無仮説を棄却することで、「差がある」という仮説を(間接的に)示しています。したがって、ごく単純に考えると「帰無仮説を棄却されれば『差がある』ということになるのだから、逆に帰無仮説を棄却されなければ『差がない』ということになる」と思えます。
しかし、この考え方は正しくありません。なぜなら、統計的仮説検定の枠組みにおいて、「帰無仮説を棄却されない」ことは「帰無仮説が正しい」ことを示すわけではないからです。そうではなく、帰無仮説を棄却されないことは「帰無仮説が正しいという前提を覆すだけの証拠はデータから得られなかった」ということが示されただけであり、「両者に差があるのかないのか、データからはっきりとは分からない」という曖昧な態度が統計的仮説検定における正しい解釈です。いうならば「証拠不十分により釈放」されているにすぎないわけです。
くわえて、百歩譲って「有意差なし=同等である」ことを認めたとすると、仮説検定の仕組みを悪用した不正を行うことが可能になってしまいます。仮説検定において帰無仮説を棄却するか否かは「統計検定量(の絶対値)の大きさ」によって決めることになっており、統計検定量が大きければ大きいほど、帰無仮説は棄却されやすくなり、逆に小さいほど、棄却されにくくなります。そして、検定統計量は「効果量」と「サンプルサイズ」に比例するという構造になっています。
このうち「効果量」の方は、自然が決めた摂理であるため、人にはどうしようもありませんが、「サンプルサイズ」の方は事前にどれくらい集めるかを決めることができます。そのため、意図的にサンプルサイズを小さくすることで「有意差なし」という結果を生み出すことができてしまうわけです。
例えば、ある新薬Aと標準薬の同等性を示すために、Aの製造元が比較試験を行い次のような結果が得られたとします。
| 治癒 | 非治癒 | 合計 | |
|---|---|---|---|
| 新薬 | $1$ | $4$ | $5$ |
| 標準薬 | $4$ | $1$ | $5$ |
| 合計 | $5$ | $5$ | $10$ |
フィッシャーの直接確率法による両側 $\mathrm{P}$値 \begin{gather} \mathrm{P}\cong0.206 \end{gather}
この結果をもって、「有意差が出なかったから同等ですね。だから安いうちの薬を買ってください」と言われても、「そうですね」と納得する人はいないでしょう。こうしたことになるので、同等性を証明するためには別のアプローチが必要になります。
同等性の示し方②:「同等性マージン」の導入
同等性の立証を考えるうえでヒントになるのが、優越性試験における「サンプルサイズの設計」での考え方です。先にも述べたように、検定統計量の構造からして、①サンプルサイズが大きすぎると「臨床的には意味のない差」であっても「統計的有意差」として検出してしまう、②サンプルサイズが小さすぎると、検出したい「臨床的に意味のある差」を「統計的有意差」として検出できないという問題が生じます。そのため、臨床的に意味のある差 $∆$ を事前に設定し、本当に効果がある場合に、それを「統計的有意差」として検出することを目的として、必要なサンプルサイズを過不足なく算出するというのが「サンプルサイズの設計」の考え方です。
同等性試験でも優越性試験の枠組みと同様に、臨床的に意味のある差 $∆$ を使用します。同等性試験の枠組みではこの差を同等性マージン equivalence margin と呼びます。同等性マージンは、いいかえれば「この程度の差であれば、違いがないとみなしてもよい程度の差」ということです。優越性試験が「同等とみなせない差がある場合にそれを検出する」という発想であるのに対し、「もとより差があるにしても、それは同等とみなすことができる範囲内であることを示す」という発想が同等性試験の基本的な方針となります。
同等性の示し方③:同等性の定式化
仮説検定としての表現
この考え方を統計的仮説検定の枠組みに則って定式化してみましょう。ここでは、実験群(A)と対照群(B)を比較する実験(試験)を考えます。それぞれの効果を表す結果変数(連続値データや発症割合など)の母数を $\theta_A,\theta_B$ とすると、実験群の対照群に対する効果の大きさ(効果量) $\delta$ の指標には、一般的に以下の3つが考えられます。
(1)差
\begin{gather}
\delta_D=\theta_A-\theta_B
\end{gather}
(2)比
\begin{gather}
\delta_R=\frac{\theta_A}{\theta_B}
\end{gather}
(3)オッズ比
\begin{gather}
\delta_{OR}=\frac{\theta_A \left(1-\theta_B\right)}{\theta_B \left(1-\theta_A\right)}
\end{gather}
ただし、オッズ比は $\theta$ が割合の場合にのみ定義される。
このとき、医学的には意味のある差とは考えられない「誤差範囲」、あるいは「同等」と考えられる範囲を以下のように設定します。
(1)差
\begin{gather}
\left[-\Delta,\Delta\right]
\end{gather}
(2)比・オッズ比
\begin{gather}
\left[1-\Delta,\frac{1}{1-\Delta}\right]
\end{gather}
つまり、評価指標に応じて、
(1)優越性試験では、
\begin{gather}
\left|\delta\right| \gt \Delta \quad \mathrm{or} \quad \left|\log{\delta}\right| \gt -\log{ \left(1-\Delta\right)}
\end{gather}
となれば、優越性が表現でき、
(2)同等性試験では、
\begin{gather}
\left|\delta\right| \le \Delta \quad \mathrm{or} \quad \left|\log{\delta}\right| \le -\log{ \left(1-\Delta\right)}
\end{gather}
となれば、同等であることが表現できます。
したがって、例えば、「差」について考えるとき、
(1)優越性試験では、
\begin{gather}
H_0: \left|\delta\right| \le \Delta \quad H_1: \left|\delta\right| \gt \Delta
\end{gather}
(2)同等性試験では、
\begin{gather}
H_0: \left|\delta\right| \geq \Delta \quad H_1: \left|\delta\right| \lt \Delta
\end{gather}
が検証すべき仮説ということになります。
このうち、同等性試験の仮説を検定する際には、この仮説を更に2つの片側検定の組み合わせとして表現し、それぞれを有意水準 $\alpha$ で検定するという手順$^\mathrm{(i)}$を取りますが、一般的には、次の信頼区間としての表現の方がよく使われています。
信頼区間としての表現
有意水準 $\alpha$ の仮説検定と信頼水準 $100 \left(1-\alpha\right)\%$ 信頼区間を構築することが同等であることを鑑みると、同等性に関する仮説検定で同等性が示されることは、差(効果量) $\delta$ の $100 \left(1-\alpha\right)\%$ 信頼区間 \begin{gather} 100 \left(1-\alpha\right)\%\ \mathrm{C.I.}: \left[\hat{\theta}\pm Z_{0.5\alpha} \cdot \mathrm{S.E.} \left(\hat{\theta}\right)\right]\\ 100 \left(1-\alpha\right)\%\ \mathrm{C.I.}: \left[\hat{\theta}\pm t_{0.5\alpha} \left(n\right) \cdot \mathrm{S.E.} \left(\hat{\theta}\right)\right] \end{gather} が 同等性を表す区間に完全に含まれること \begin{gather} \mathrm{C.I.}\in \left[-\Delta,\Delta\right] \end{gather} とほぼ同義になります$^\mathrm{(ii)}$。
これを図で表すと、以下のようになります。なお、これまでの中で「比・オッズ比」を用いる場合には、$\delta\rightarrow\log{\delta},\ \Delta\rightarrow\log{ \left(1-\Delta\right)}$ と置き換えます。
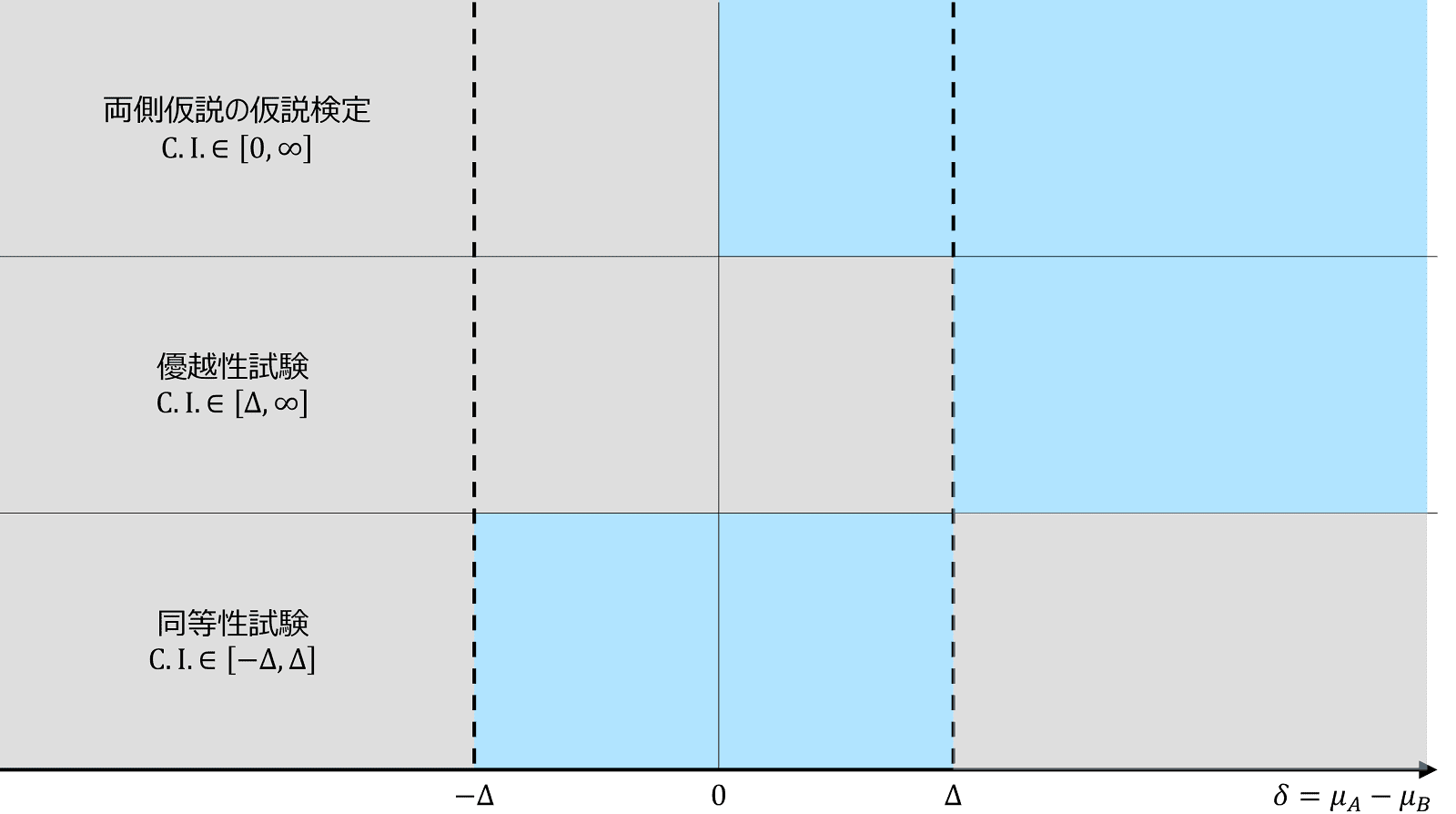
非劣性試験
このように、同等性を示す場合には信頼区間の下限・上限ともに同等性マージンの中にスッポリ入ることが必要ですが、そのためには信頼区間がかなり小さくなるように症例数を十分多くとることが必要です。しかし、臨床研究でそのような十分な症例数を確保するのは難しいことが少なくありません。
その打開策として登場したのが非劣性試験です。非劣性試験 non-inferiority trials は、同等性試験と基本的な考え方は同じで、安全性や費用などの面が標準治療よりも優れている際に「治療効果は、少なくとも許容できる以上には劣っていない」、すなわち「非劣性」を示そうとする研究デザインです。
「非劣性」の基本的な示し方は「同等性」の場合と同様で、「臨床的に意味のある差」を非劣性試験の枠組みでは非劣性マージン non-inferiority margin と呼びます。非劣性マージンは「仮に劣っていたとしても、許容できる差」という意味であり、「少なくとも許容できる以上に劣ることはない」ことを示すという発想が非劣性試験の基本的な方針となります。
非劣性の定式化
非劣性試験を定式化する際の基本的な考え方は「同等性」の場合と同様ですが、同等性試験は、信頼区間の上限と下限の両方に関心があった(両側信頼区間)のに対し、非劣性試験では「劣っている場合でも許容できる以上には劣らない(優れている分には、いくら優れていてもいい)」ことを示すことが目標なので、下限のみに着目します。
この意味で、仮説検定としての表現は本質的に片側検定 \begin{gather} H_0:\delta \le -\Delta \quad H_1:\delta \gt -\Delta \end{gather} となります。
信頼区間で表現する場合、理論的には片側信頼区間を求めることになりますが、慣習的に両側信頼区間を報告する論文があるため、注意が必要です。 \begin{gather} \mathrm{C.I.}\in \left[-\Delta,\infty\right] \end{gather}
同等性試験と非劣性試験の関係
同等性試験と非劣性試験はどちらも優越性を示すことを目的としておらず、どちらも「劣っていたとしてもそれは許容範囲内」ということを示すことは共通しています。しかし、同等性は「良かったとしても無視できるだけの差しかない」ということを示すいっぽう、非劣性は「良い分にはいくらよくてもかまわない」というスタンスです。この点、非劣性の考え方は「良い場合は、もしかしたら優越性を示すことになるかもしれない」という希望的な可能性を残しています。「悪い場合」のことは共通しており、「良い場合」にはさらに有利なことを示せる可能性がある分、非劣性の方がより好ましいと考えることもできます。
くわえて、本質的に両側性である同等性試験よりも、片側性である非劣性試験の方が、サンプルサイズを抑えることができます。このため、同等性試験と非劣性試験を比べた場合、非劣性試験がより多く選ばれる傾向にあります。
優越性試験と非劣性試験の関係
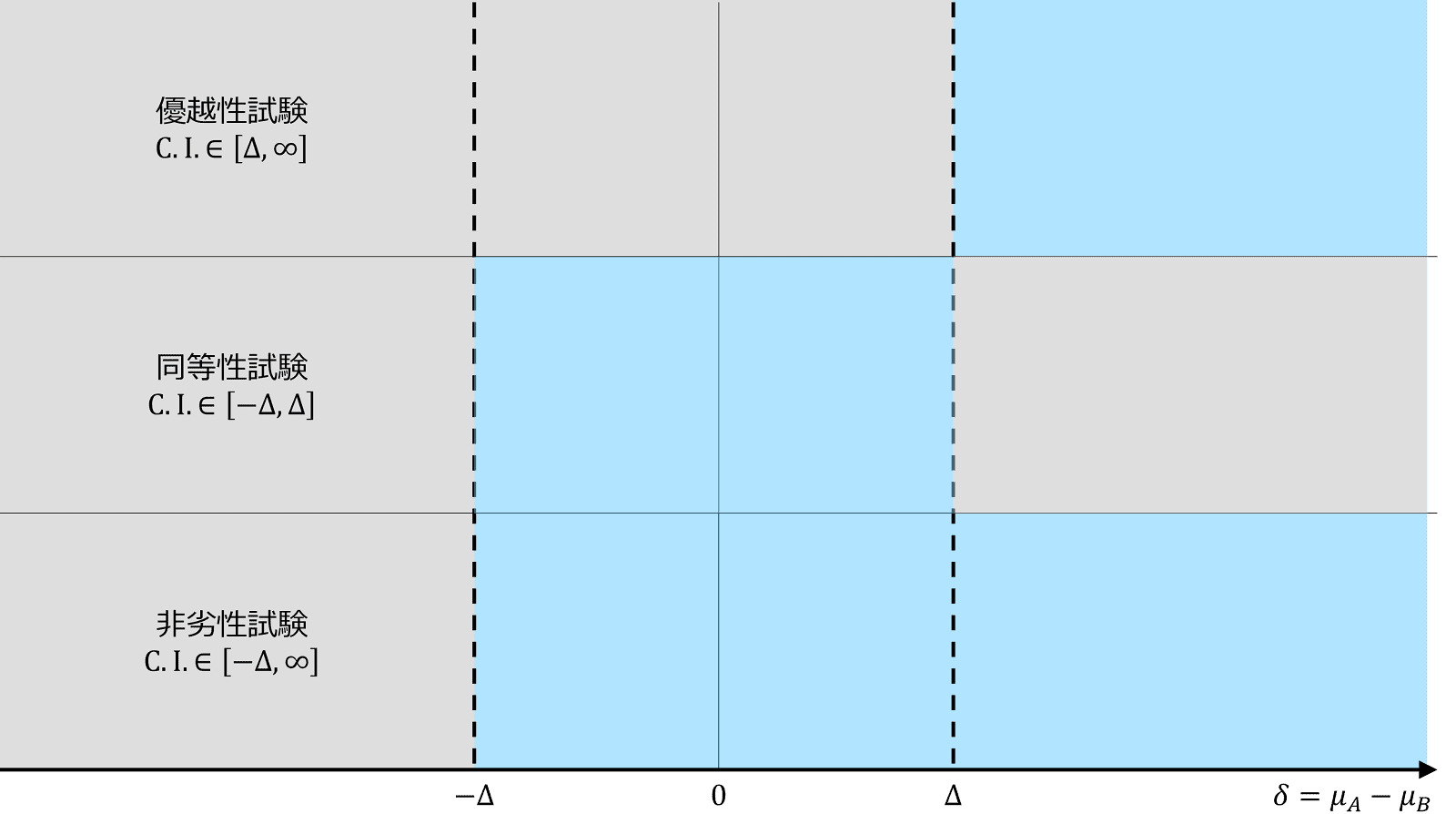
非劣性マージンは、統計解析のうえでは一種のハンディキャップとして働いています。すなわち、非劣性マージンの値が大きいほど、非劣性が証明されやすくなります。また優越性と比べると、非劣性の方が示しやすいという関係があります。以下の図に表されるように、非劣性は優越性の範囲を完全に含んでおり、非劣性が成り立つ範囲が優越性よりも広いことがその理由です。
優越性・同等性・非劣性の信頼区間
最後に、優越性・同等性・非劣性の信頼区間についてまとめたいと思います。基本的には次のように考えると、分かりやすいと思われます。
優越性:信頼区間の下限が臨床的有意差よりも大きい($\Delta$ をまたがない)。
同等性:信頼区間の下限と上限(両側)が同等性マージンの中にすべて入る。
非劣性:信頼区間の下限が非劣性マージン(片側)より大きい($-\Delta$ をまたがない)。
これを図で表すと以下のようになります。
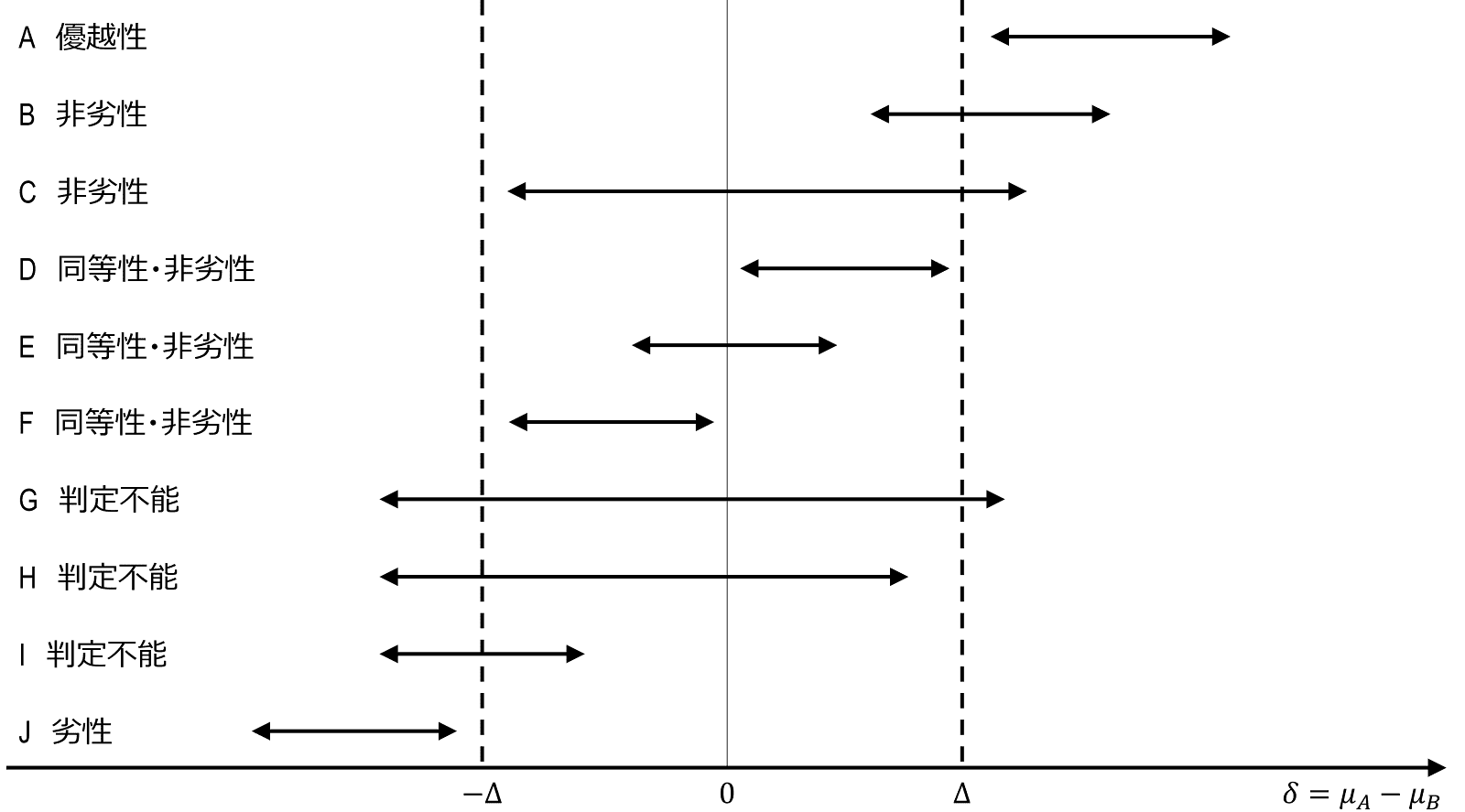
参考文献
- スティーブン・ハリー, スティーブン・カミングス ほか 著, 木原 雅子, 木原 正博 訳. 医学的研究のデザイン:研究の質を高める疫学的アプローチ. メディカル・サイエンス・インターナショナル, 2014, p72-73, p.177-179
- 新谷 歩 著. 今日から使える医療統計. 医学書院, 2015, p.151-157
- 丹後 俊郎, 松井 茂之 編集. 医学統計学ハンドブック 新版. 朝倉書店, 2018, p.331-345
- Morikawa, T. & Yoshida, M.. A useful testing strategy in phase III trials: combined test of superiority and test of equivalence. J Biopharm Stat. 1995, 5(3), p.297-306, doi: 10.1080/10543409508835115
- 小柳 貴裕. 統計学 整形外科医が知っておきたい(08)同等性(非劣性)の検証:帰無仮説採択の誤解. 臨床整形外科. 2003, 38(7), p.905-910.
- Piaggio, G., Elbourne, D.R., Pocock, S.J. et al.. Reporting of noninferiority and equivalence randomized trials: extension of the CONSORT 2010 statement. JAMA. 2012, 308(24), p.2594-2604, doi: 10.1001/jama.2012.87802
- Walker, J.. Non-inferiority statistics and equivalence studies. BJA education. 2019, 19(8), p.267-271, doi: 10.1016/j.bjae.2019.03.004
- Leung, J.T., Barnes, S.L., Lo, S.T. et al.. Non-inferiority trials in cardiology: what clinicians need to know. Heart. 2020, 106(2), p.99-104, doi: 10.1136/heartjnl-2019-315772
引用文献
- Doi, J.A.. Introduction to intersection-union tests. 2012, https://www.researchgate.net/profile/Jimmy-Doi/publication/255609707_INTRODUCTION_TO_INTERSECTION-UNION_TESTS/links/0c96053bd83e39f350000000/INTRODUCTION-TO-INTERSECTION-UNION-TESTS.pdf.
- Berger, R.L.. Multiparameter Hypothesis Testing and Acceptance Sampling. Technometrics. 1982, 24(4), p.295-300, doi: 10.2307/1267823
- Hsu, J.C., Gene Hwang, J.T., Liu, Hung-Kung et al.. Confidence Intervals Associated with Tests for Bioequivalence. Biometrika. 1994, 81(1), p.103-114, doi: 10.2307/2337054
- 丹後 俊郎, 松井 茂之 編集. 医学統計学ハンドブック 新版. 朝倉書店, 2018, p.336
脚注
- 同等性の検定を片側検定の組み合わせとして表現すると、以下のようになります。 \begin{gather} H_0: \left(\delta \le -\Delta\right)\cup \left(\delta \geq \Delta\right)\Leftrightarrow\delta \le -\Delta \quad \mathrm{or} \quad \delta \geq \Delta\\ H_1: \left(\delta \gt -\Delta\right)\cap \left(\delta \lt \Delta\right)\Leftrightarrow-\Delta \lt \delta \lt \Delta \end{gather} このとき、IUT(intersection-union test)$^\mathrm{(1)}$の考え方を利用すると、この帰無仮説 $H_0$ が棄却されることは、次の2つの片側検定のいずれも有意水準 $\alpha$ で棄却されることと同値となります。 \begin{gather} H_0:\delta \le -\Delta \quad H_1:\delta \gt -\Delta\\ \mathrm{and}\\ H_0:\delta \geq \Delta \quad H_1:\delta \lt \Delta \end{gather}
- 厳密に言うと、厳密にはこの区間は必ずしも有意水準 $\alpha$ の同等性検定に対応せず$^\mathrm{(2,3)}$、正確な信頼区間は、
\begin{gather}
\left[ \left\{\hat{\delta}-t_\alpha \left(n\right) \cdot \mathrm{S.E.} \left(\hat{\delta}\right)\right\}^-,\ \left\{\hat{\delta}+t_\alpha \left(n\right) \cdot \mathrm{S.E.} \left(\hat{\delta}\right)\right\}^+\right]
\end{gather}
ここで、
\begin{gather}
x^-=\mathrm{min} \left\{0,x\right\},\ x^+=\mathrm{max} \left\{0,x\right\}
\end{gather}
となります。
通常の $100 \left(1-2\alpha\right)\%$ 信頼区間が0を含めばこの信頼区間と一致します。ただ、
同等性の意思決定に関するかぎり、通常の信頼区間と正確な信頼区間は同じ結論が得られ、信頼区間としての価値から判断すると、通常の信頼区間を利用することが望ましい
$^\mathrm{(4)}$とされています。



0 件のコメント:
コメントを投稿