標本調査の結果にもとづいて統計的推論をする際、標本平均や標本不偏分散などの統計量を用いて推定や仮説検定を行いますが、これらの手法に妥当性を与える根拠となるのが、標本分布に関する理論です。本稿では、そうした標本分布の概要について解説しています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
母集団と母集団分布
標本調査を行う目的は、その結果にもとづいて「母集団についての傾向や法則について、統計的推論を行うこと」でした。例えば、「ある地域に住む人々」を母集団として、その「身長」について知りたいとすると、さまざまな身長の値が観測されるでしょう。このとき、ある人の身長がいくつであるかは分かりませんが、全体調査を行えば、確実に「ある範囲の身長を取る確率」は算出することができます。そうした意味で、「ある人の身長」は確率変数であり、「ある地域に住む人々の身長の分布」は、確率分布であるといえます。つまり、「母集団についての情報」は、その母集団の「分布」というかたちで具体化されます。これを母集団分布 population distribution と呼び、標本調査の目的は、「母集団分布を特定する」という問題に置き換えることができます。
一般的に、統計的推論を行う際には、「標本として集められる確率変数 $X_1,X_2, \cdots ,X_n$ は、ある確率分布 $f \left(x\right)$ からの互いに独立な確率変数である」との前提のもとで行います。
母集団分布の母数:パラメトリック・ノンパラメトリック
各標本の値は、母集団分布に従ってばらついています。実際の分析においては、この母集団分布についての事前の仮定によって2つの場合があります。
1つ目は、母集団分布がある知られた確率分布であることが、理論的・経験的にわかっている場合です。例えば、交通事故による1日当たりの死亡者数は、死亡事故の発生確率が非常に小さいことから、少数の法則によってポアソン分布に従うと考えられます。
つまり、標本 $X_1,X_2, \cdots ,X_n$ は、互いに独立に、ある定数 $\lambda$ を持ったポアソン分布 $\mathrm{Po} \left(\lambda\right)$ に従い、各 $\mathrm{P} \left(X_i=x\right)$ は
\begin{align}
f \left(x\right)= \left\{\begin{matrix}\displaystyle\frac{\lambda^xe^{-\lambda}}{x!}&x=0,1,2, \cdots \\0&\mathrm{other}\\\end{matrix}\right.
\end{align}
であり、
この定数えさえわかれば、母集団分布についてすべて知ることができます。このように、事前に母集団分布が○○分布という形で与えられており、いくつかの定数さえわかれば、母集団分布についてすべて知ることができる場合、それをパラメトリック parametric の場合と呼びます。ここでは母集団分布を決定する定数が求めるべきものであり、統計的推測ではこの定数を母数 parameter と呼びます。
2つ目は、母集団分布の具体的な形が、事前に知られていない場合です。たとえば、世界各国の面積や人ロの分布などがこの例です。この場合は、第1の場合と異なり、いくつかのパラメータで母集団分布を決定することはできません。このような場合をノンパラメトリック nonparametric の場合と呼びます。この場合は、母集団分布にかかわらず広く定義できるパラメータで母集団分布を分析します。これには、分布の位置に関するパラメータとして、母集団の平均、中央値、最頻値など、ばらつきに関するものとして母集団の分散、範囲など、分布の形に関するものとして歪度や尖度を考え、分析を行います。
統計量
母集団分布を特定する際、母集団の平均、中央値、最大値、最小値などの代表値、あるいは分散や範囲、四分位範囲などの散布度が関心の対象となります。これらの値を標本調査の結果から推測するのはどうすればよいかといえば、基本的には「得られたデータから対応する値を求める」という単純な方法で問題ありません。例えば、母平均が知りたいのであれば、標本平均を求め、それを母平均の推定値として採用します。ここでの標本平均のように、標本を要約し、母集団の母数のいろいろな推測に使われるものを統計量 statistic と呼びます。
標本平均と標本(不偏)分散
先述したように、母集団の母数には、最大値、中央値、範囲などさまざまな種類がありますが、多くの統計的推論において、標準的に使われるのが、次の標本平均 sample mean と標本分散 sample variance・標本不偏分散 sample unbiased variance です$^\mathrm{(i)}$。
標本平均
\begin{gather} \bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_i \end{gather}
標本分散・標本不偏分散
標本分散 \begin{gather} S^2=\frac{1}{n}\sum_{i=1}^{n} \left(X_i-\bar{X}\right)^2 \end{gather} 標本不偏分散 \begin{gather} s^2=\frac{1}{n-1}\sum_{i=1}^{n} \left(X_i-\bar{X}\right)^2 \end{gather}
標本分散と標本不偏分散の違いは、割る数がデータの個数 $n$ かそこから1を引いた値 $n-1$ かの違いです。最も単純に考えれば標本分散でいいように思われますが、推定量としての「不偏性」という性質を有していることから、基本的に標本不偏分散の方が用いられており、単に「標本分散」というと、多くの場合でこの「標本不偏分散」のことを指しています。
標本分布
ではここで、ある内閣の支持率について推測する場合を考えてみましょう。この場合、母集団は「ある国の有権者全体」となり、関心のあるパラメータは「支持率 $p$」ということになります。このような場合、母集団分布として二項分布を想定することが可能で、確率変数 $X_i$ は「支持する」ならば「1」、「支持しない」ならば「0」の値を取るベルヌーイ試行であると考えられます。このとき、標本 $X_1,X_2, \cdots ,X_n$ のうち、「支持する」の人数は、 \begin{gather} X=X_1+X_2+ \cdots +X_n \end{gather} となり、 支持率は、標本比率 \begin{gather} \hat{p}=\frac{X}{n} \end{gather} から推測することができます。
ただ、支持者の人数 $X$ や標本比率の値 $\hat{p}$ は、どの $n$ 人を調査するかによって、毎回変わってくると予想されます。いいかえれば、標本を抽出するたびに統計量の値が変動するという意味で、統計量もまた確率変数であり、それに対応した確率分布があるということになります。この確率分布をその統計量の標本分布 sampling distribution と呼びます。
大数の法則:標本比率の場合
例えば、母集団における内閣支持率が40%、すなわち $p=0.4$ であるとします。この母集団から5人の標本を選んで($n=5$)支持者の数 $X$ を調べるとすれば、$X$ は $0,\ 1,\ 2,\ 3,\ 4,\ 5$ のいずれかの値となり、したがって標本の中の支持者の割合 $\hat{p}=\frac{X}{n}$ は、どのような5人が選ばれるかによって、$0,\ 0.2,\ 0.4,\ 0.6,\ 0.8,\ 1$ と6通りの異なる値をとり得ます。
母集団比率 $p$ の値を標本比率 $\hat{p}$ で推測しようとするとき、当然それは常に正しいというわけではありません。ただ、それが正しい($\hat{p}=p=0.4$)確率は0.346であり、$\hat{p}$ が $p$ の真の値0.4からどれくらい外れているか、すなわちどれだけの誤差をもち、またその確率がどれくらいあるかということも分かります。
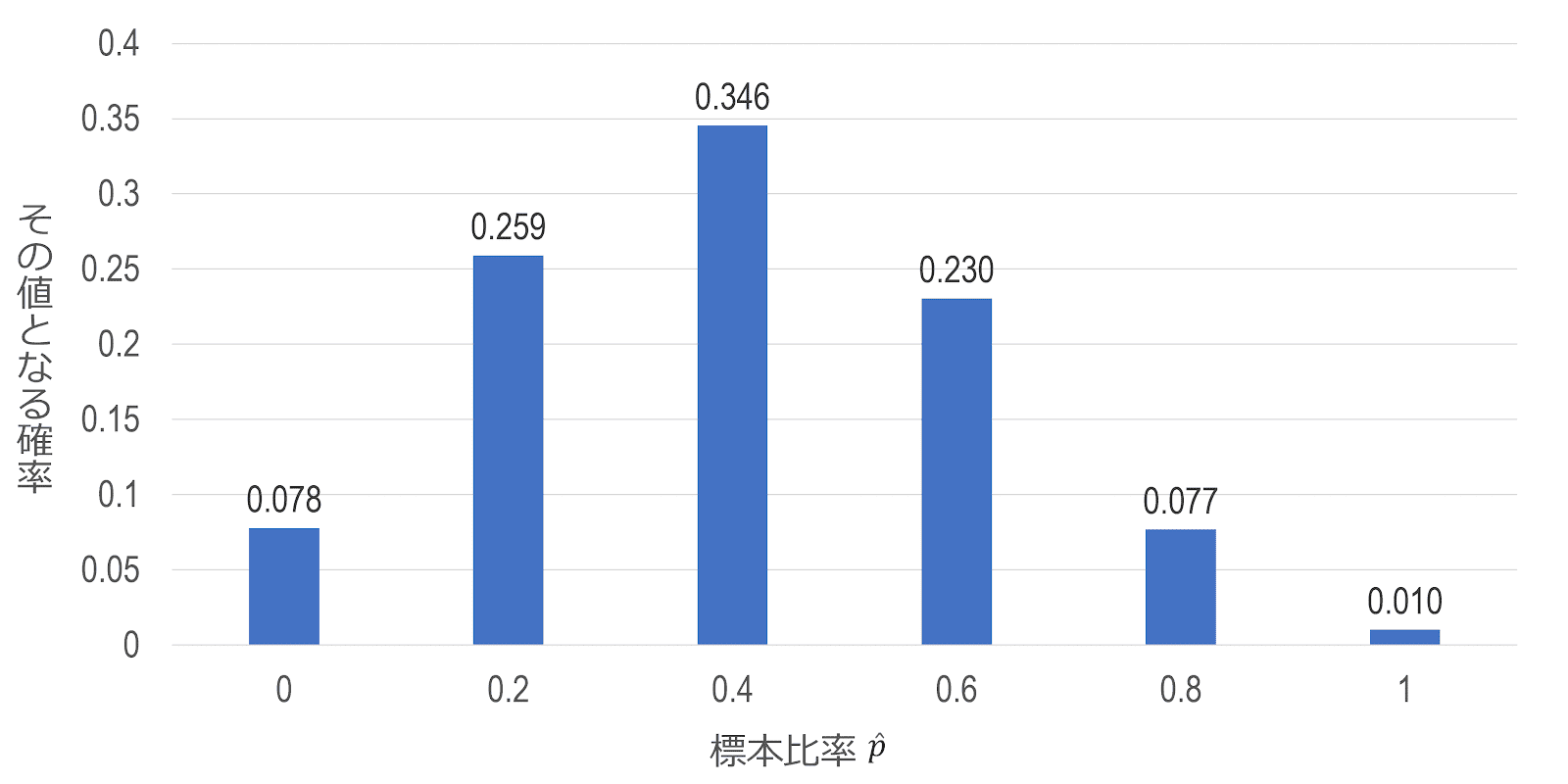
では、ここからサンプルサイズを大きくしていくとどうなるかを見てみましょう。ここでは真の値付近である $0.4\pm0.1$ の範囲に注目すると、標本比率がこの範囲に収まる確率は、 \begin{gather} n=30 \quad \mathrm{P} \left(0.3 \le \hat{p} \le 0.5\right)\cong0.886\\ n=40 \quad \mathrm{P} \left(0.3 \le \hat{p} \le 0.5\right)\cong0.920\\ n=50 \quad \mathrm{P} \left(0.3 \le \hat{p} \le 0.5\right)\cong0.940\\ n=100 \quad \mathrm{P} \left(0.3 \le \hat{p} \le 0.5\right)\cong0.983 \end{gather} となり、 サンプルサイズが大きくなるほど、標本比率が $0.3 \le \hat{p} \le 0.5$ の範囲内に収まる確率が高くなっていくことが分かります。こうした現象は、大数の法則として知られています。
大数の法則 law of large numbers は一般に標本統計量と母数との差は、サンプルサイズが大きくなるほど小さな値を取る確率が高まっていくということを示しています。これは例えば、母平均を推定したい場合「大標本では、観察された標本平均を母集団の真の平均(母平均)とみなしてよいだろう」という直感を、数学的に厳密に証明したものにほかなりません。
標本平均の分布:期待値と分散
独立な確率変数の期待値と分散の性質を用いると、母集団分布によらず、標本平均 $\bar{X}$ の期待値と分散は以下のようになります。
期待値の性質 $E \left(\sum_{i=1}^{n}{aX_i}\right)=a\sum_{i=1}^{n}E \left(X_i\right)$ より、 \begin{align} E \left(\bar{X}\right)&=E \left[\frac{1}{n}\sum_{i=1}^{n}X_i\right]\\ &=\frac{1}{n}E \left(\sum_{i=1}^{n}X_i\right)\\ &=\frac{1}{n} \left\{\sum_{i=1}^{n}E \left(X_i\right)\right\}\\ &=\frac{1}{n} \cdot n\mu\\ &=\mu \end{align}
分散の性質 $V \left(\sum_{i=1}^{n}{aX_i}\right)=a^2\sum_{i=1}^{n}V \left(X_i\right)$ より、 \begin{align} V \left(\bar{X}\right)&=V \left[\frac{1}{n}\sum_{i=1}^{n}X_i\right]\\ &=\frac{1}{n^2}V \left(\sum_{i=1}^{n}X_i\right)\\ &=\frac{1}{n^2} \left\{\sum_{i=1}^{n}V \left(X_i\right)\right\}\\ &=\frac{1}{n^2} \cdot n\sigma^2\\ &=\frac{\sigma^2}{n} \end{align}
このことから、標本平均 $\bar{X}$ の期待値は母平均 $\mu$ になるいっぽう、分散は母分散よりも小さい $\frac{\sigma^2}{n}$ になることが分かります。標本平均に限らず、一般に母数の推定量の標準偏差のことをその統計量の標準誤差 standard error と呼びます。標本平均の場合は、$\frac{\sigma}{\sqrt n}$ が標本平均の標準誤差 staridard error of the mean ということになります$^\mathrm{(ii)}$。
また、この式の形から標準誤差は、①母標準偏差 $\sigma$ に比例し、②サンプルサイズ $\sqrt n$ に反比例することも分かります。これは、次のように考えると、感覚的にも理解できます。すなわち、例えば身長を例にとると、①については、母集団の中の人たちの身長が似たようなものでみな $\mu$ に近い値であれば($\sigma^2$ が小さい)、標本に選ばれる人たちの身長もほぼ同じようなものであり、したがってその平均値 $\bar{X}$ も $\mu$ に近い値となるでしょう。すなわち、$\bar{X}$ の分散は小さくなります。しかし、母集団の中人たちの身長がまちまちであれば($\sigma^2$ が大きい)、標本に選ばれた人たちの中にたまたま平均値よりもかなり大きい人が多かったり、あるいは小さい人が多かったりすることがあり、その結果、標本平均が $\mu$ よりかなり大きかったり、小さかったりします。すなわち、$\bar{X}$ の分散が大きくなります。
次に②について、標本に選ばれる人数が少なければ、選ばれた人たちがたまたま大きい人たちばかりだったり、逆に小さい人ばかりであったりする可能性があり、$\bar{X}$ は大きくなったり小さくなったりして、分散は大きくなります。しかし、選ばれる人数が多くなれば、大きい人や小さい人が混じって選ばれる可能性が高くなり、たまたま大きい人ばかり、あるいは小さい人ばかり選ばれて、$\bar{X}$ が $\mu$ から大きくはずれる可能性は小さくなります。すなわち $\bar{X}$ の分散は小さくなります。
中心極限定理
標本平均の分布の期待値と分散が理論的にどうなるかは分かりましたが、同じ期待値と分散をもつ分布であっても、正規分布、ポアソン分布、指数分布など分布の種類によって、その形状は大きく異なります。この点、もし母集団が正規分布であれば、正規分布の再生性から、標本平均の分布も正規分布となります。
ただ、世の中には正規分布に従わない確率変数も数多くあり、既存の理論分布のどれにも当てはまらない名もなき分布は数多くあります。そのような分布から得られた標本である場合、標本平均の分布がどんな形をしているのかは見当もつかないように思えます。
しかしこの点、サンプルサイズが十分に大きい場合、母集団分布が何であるかによらず、標本平均の分布は正規分布になることが知られています。 \begin{align} \bar{X}\xrightarrow[]{d}\mathrm{N} \left(\mu,\frac{\sigma^2}{n}\right) \end{align}
この法則は、中心極限定理 central limit theorem として知られており、主要な統計的方法の多くはこの定理に基礎を置いています。中心極限定理の強力な点は、母集団分布によらない、すなわち母集団分布が何であっても成立するという点にあり、サンプルサイズさえ十分に集めることができれば、単純に標本平均を求めてそれらを比較すればいいというふうに事態を単純化できます。母集団分布に関する前提を必要とないところが、非常に便利であるといえます。
参考文献
- 東京大学教養学部統計学教室 編. 基礎統計学 1 統計学入門. 東京大学出版会, 1991, p.155-172, p.182-186
- ダグラス・アルトマン 著, 木船 義久, 佐久間 昭 訳. 医学研究における実用統計学. サイエンティスト社, 1999, p.132-134
- 宮川 公男 著. 基本統計学 第4版. 有斐閣, 2015, p.181-212
- 新谷 歩 著. 今日から使える医療統計. 医学書院, 2015, p.7-10
脚注
- 平均と分散が用いられる理由には、①母集団分布の位置と形状に関する要約統計量であり、②正規分布の場合、この2つが分かれば、母集団分布の特性を完全に表せるなどがあります。
- 基本的には「標準誤差」という概念は総称であり、標本平均だけに使う概念ではありませんが、標本平均を問題とすることがとても多いため、標準誤差というと、標本平均の標準誤差を指すことが多いです。別の推定値に伴う別種の標準誤差がありますが、平均値の標準偏差は標準誤差(SE、SEM)と省略されることがよくあり、普通はこうしても曖昧になりません。



0 件のコメント:
コメントを投稿