科学研究や社会的な調査などでは、データを収集し、得られたデータを分析することで、母集団に関する法則を見出すことを目的としています。データを分析するためには、まず、得られたデータを整理・要約する必要があります。本稿では、そのような「データの整理・要約」の方法論である記述統計学について、解説しています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
記述統計学とは?
科学研究や社会的な調査などでは、関心のある母集団に関する何らかの法則を見出すことを目的としています。そのための方法として、全数調査と標本調査がありますが、どちらの方法であっても、得られたデータから「情報」を引き出さなければなりません。
情報を引き出すプロセスは、通常、2段階で構成されます。すなわち、①集められたデータを分かりやすいかたちで整理・要約する段階と②要約された情報をもとに、分析や解析を行うことで、目的としている「母集団に関する法則」に関する知見を見出す段階です。これらの2段階は、①は記述統計学、②は分析統計学や推測統計学などと呼ばれています。
実験や調査などの観測 observation の中では数多くのデータが得られますが、ひとつひとつを丹念に見ているだけでは、その背後にある「全体」が見えてこず、果てしない作業に追われることになります。それゆえに、データを「正しく」、かつ「効率的」に読む必要があります。
このようなデータの「読み方」(情報の効率的な引き出し方)の方法論が記述統計学 descriptive statistics です。すなわち、記述統計学とは「集団としての特徴を記述するために、観測対象となった各個体について観測し、得られたデータを整理・要約する方法」であり、狭義には「ある1回の観測の結果それ自体だけについての分析、ある特定の観察結果それ自体の分析」を指します。
本稿では、そのような「得られたデータの整理・要約のしかた」についての基本的な事項を解説していきます。
データのチェックと外れ値
データを集めた後、最初にすることは、データの中に間違いや外れ値がないかどうかを確認することです。分類データの場合、例えば、血液型に次のような4コード 1=A 2=B 3=O 4=AB と対応させていれば、 0や5、6、7、8といった値が入力されていれば、それは間違い(入力ミス)ということが分かります。こうした場合、「取り得ない値」を取っており、明らかに「間違い」だと判断できるため、可能であれば修正し、それができなければ削除します。
いっぽう、連続データの場合、そうした判断が難しいことがあります。例えば、小学生5年生10人の身長のデータとして次のようなデータが得られたとします。 \begin{align} \boldsymbol{x}= \left\{145.6,\ 145.2,\ 148.3,\ 146.2,\ 142.3,\ 147.6,\ 137.4,\ 148.8,\ 149.9,\ 180.3\right\} \left[\mathrm{cm}\right] \end{align}
この場合、最初の9個の値は「あり得る値」と認識できますが、最後の 180.3 cm という値は、ほかに比べて飛びぬけています。このように、他の値と比べて極端に小さい・大きい値のことを外れ値 outlier と呼びます。また、外れ値と似た概念に、「異常値」があります。異常値 abnormal value とは「しかるべき理由により他のデータとは異質と考えられ、修正あるいは削除すべきと判定されるデータ」を指します。
180.3 cm という値の場合、確かに小学5年生の身長としては、飛びぬけていますが、数万人、数十万人に1人くらいそうした人がいても不思議ではなく、生物学的に「あり得ない値」(その値を取る可能性がない値)というわけではありません。これが例えば、14.65 cm という値であれば、生物学的に「あり得ない値」と考えられるため、入力ミスによる異常値である可能性が疑われます。
外れ値の対処方法
外れ値は、後に見るような要約統計量の算出や統計的な解析の結果に大きな影響を与える可能性があるものですが、無条件に除外してしまうと、それはそれでバイアスとなり、推測を歪める原因となります。そのため、データの中に外れ値があった場合、まず、外れ値の原因を調べ、それが異常値かどうかを判断することが基本となります。
外れ値がほぼ確実に異常値であると判断される場合、修正する、あるいは、修正できなければ削除します。これに対し、外れ値が異常値でない場合や異常値であるかどうかわからない場合、そうした極端な値の影響を受けにくい要約や解析の方法を選ぶという対処が考えられます。
質的データの記述
疫学における横断研究や国勢調査など、「現状の把握」を目的とする調査・研究でも、医学や心理学などにおける「仮説検証的な」調査・研究でも、集めたデータは、そのデータの型によってまとめ方や解析手法が規定されます。
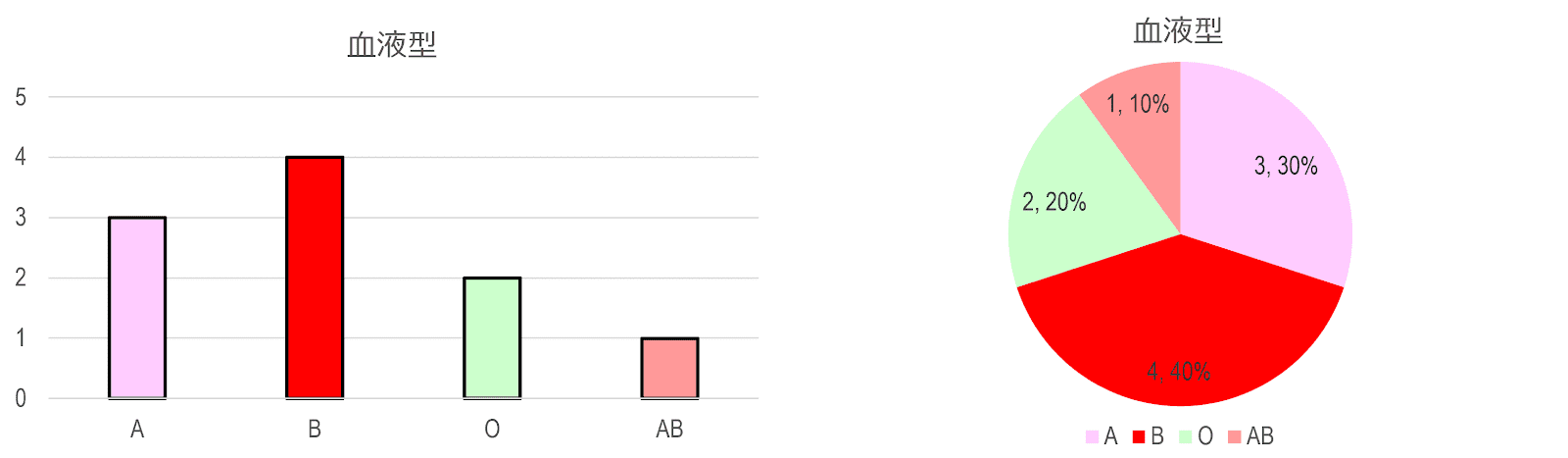
質的データ(名義尺度・順序尺度)は、その性質から、単純に各カテゴリーの出現頻度を集計して、分布を把握します(逆に、得られた値の四則演算などはしても意味がない)。通常、各カテゴリーの出現数や相対度数(全体のうち、そのカテゴリーが占める割合)を示すと分かりやすくなります。棒グラフ bar chart や円グラフ pie chart, circle chart で図示すると、より分かりやすいでしょう。
| No. | 血液型 | 成績 |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 1 | 1 |
| 3 | 1 | 5 |
| 4 | 2 | 3 |
| 5 | 2 | 2 |
| 6 | 4 | 1 |
| 7 | 3 | 2 |
| 8 | 3 | 1 |
| 9 | 1 | 5 |
| 10 | 2 | 4 |
血液型(名義尺度) 1=A 2=B 3=O 4=AB 成績(順序尺度) 1=不可 2=可 3=良 4=優 5=秀
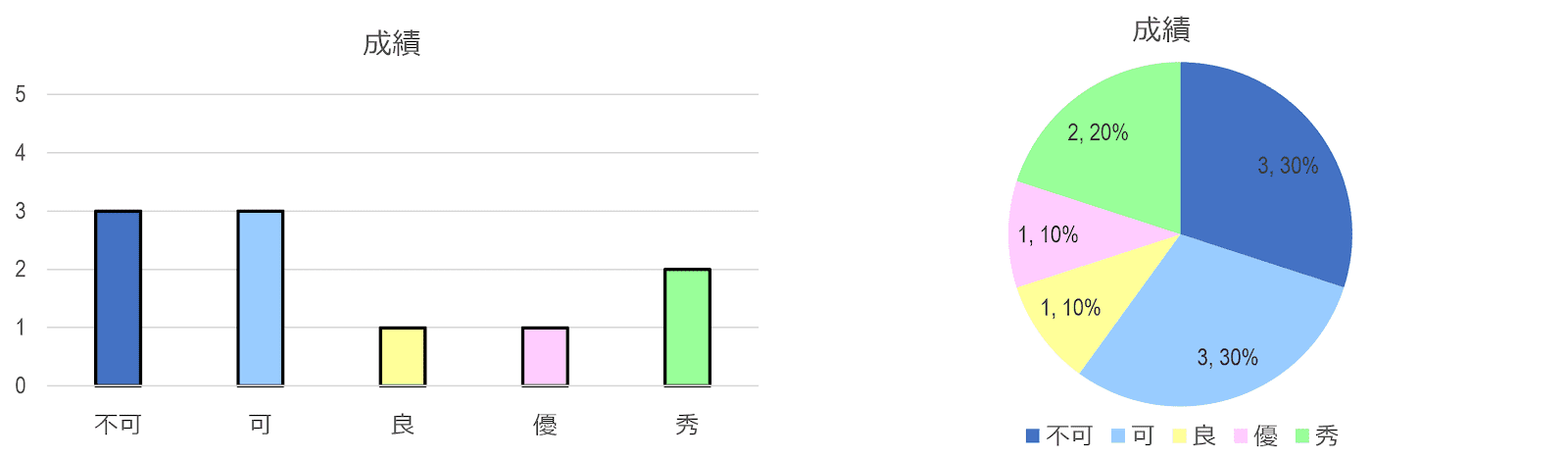
量的データの記述:度数分布表
カテゴリー数が多い順序カテゴリーデータ、計数データや連続データに対しては、最初に度数分布表を作ることから始めます。例えば、100人を対象として行ったある100点満点の試験の点数のデータとして、次のようなデータが得られたとします。
このデータは、以下のようにまとめることができます。
| 階級 | 度数 | 相対 度数 | 累積 度数 | 累積 相対度数 |
|---|---|---|---|---|
| 0 - 10 | 2 | 0.02 | 2 | 0.02 |
| 10 - 20 | 6 | 0.06 | 8 | 0.08 |
| 20 - 30 | 8 | 0.08 | 16 | 0.16 |
| 30 - 40 | 12 | 0.12 | 28 | 0.28 |
| 40 - 50 | 21 | 0.21 | 49 | 0.49 |
| 50 - 60 | 21 | 0.21 | 70 | 0.7 |
| 60 - 70 | 12 | 0.12 | 82 | 0.82 |
| 70 - 80 | 8 | 0.08 | 90 | 0.9 |
| 80 - 90 | 5 | 0.05 | 95 | 0.95 |
| 90 - 100 | 5 | 0.05 | 100 | 1 |
| 合計 | 100 | 1 |
このように、観測値のとりうる値をいくつかの階級 class に分け、それぞれの階級に入るデータの数(度数 frequency)を数えて、表にしたものを度数分布表 frequency distribution table といいます。
相対度数 relative frequency は観測値の総数、すなわちデータ全体の大きさを1としたときの、各階級に属する観測値の個数の全体中での割合を示します。これはとくに、データの大きさが異なる複数のデータの分布の比較を行うときに有効です。たとえば、別の年の同じ試験の成績の得点分布と、この分布を比較するとき、受験者数が異なるときは相対度数を用いて分布の比佼を行えばよいということになります。
累積度数 cumulative frequency、累積相対度数 cumulative relative frequency とは、度数を下の階級から順に積み上げたときの度数、相対度数の累積和です。データによっては、度数・相対度数より累積度数や累積相対度数の方が、意味があることがあります。所得分布はその例であり、たとえば400万円以上450万円未満の世帯の割合よりは、450万円未満の世帯が全体の何%かといった方が現実にはよく問題となります。
ヒストグラム
度数分布表から度数あるいは相対度数を棒グラフ状に図示したものをヒストグラム histogram といいます。ヒストグラムは連続型データの場合には、横軸に観測値のとりうる値(この場合、0点から100点まで)をとり、それぞれの階級に対して階級幅を横幅とし柱の面積が度数と比例するように高さを定めます。この例の場合には、すべての階級の階級幅が等しいので柱の高さが度数と比例します。ヒストグラムから、この試験得点の分布は、50点付近がもっとも高い、ほぼ左右対称の山型分布であることが分かります。
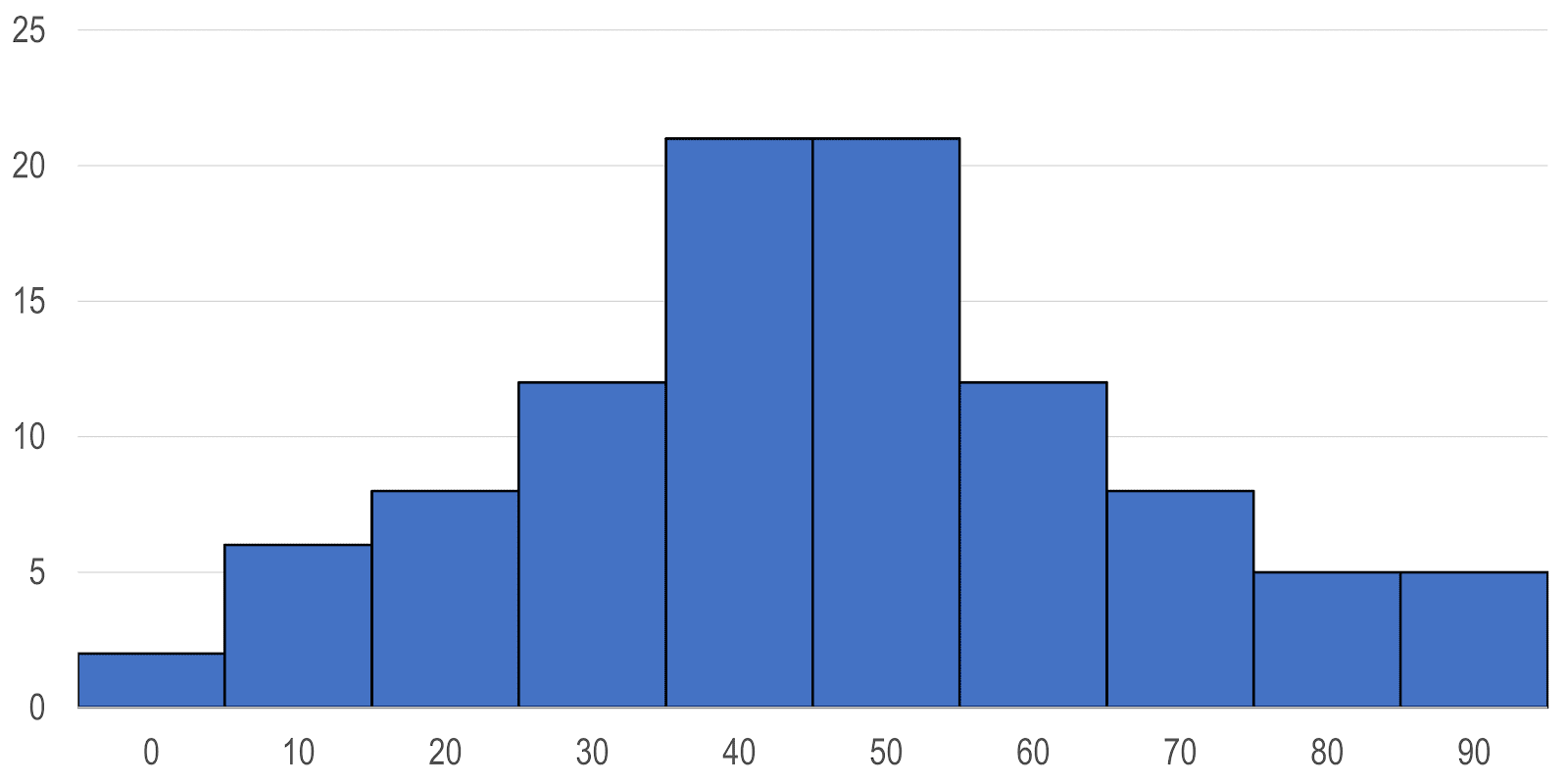
データの分布の形をみるには度数分布表をグラフにした方が、データの意味するところが一目瞭然となります。後で述べるように、要約統計量からはこのような分布の形状を確認することはできず、分布の形状によって、適切な統計量や解析の方法が違ってくるため、データを整理するにあたっては、まず、ヒストグラムを描き、分布の形状を確認することが肝心です。
分布の形状
度数分布表を作り、ヒストグラムを描くことによって、分布形を知ることができます。その結果として得られる分布には、さまざまな形があります。たとえば、試験成績の分布は先ほど見たように、中央に1つ峰がある山型の分布(単峰型 unimodal)です。
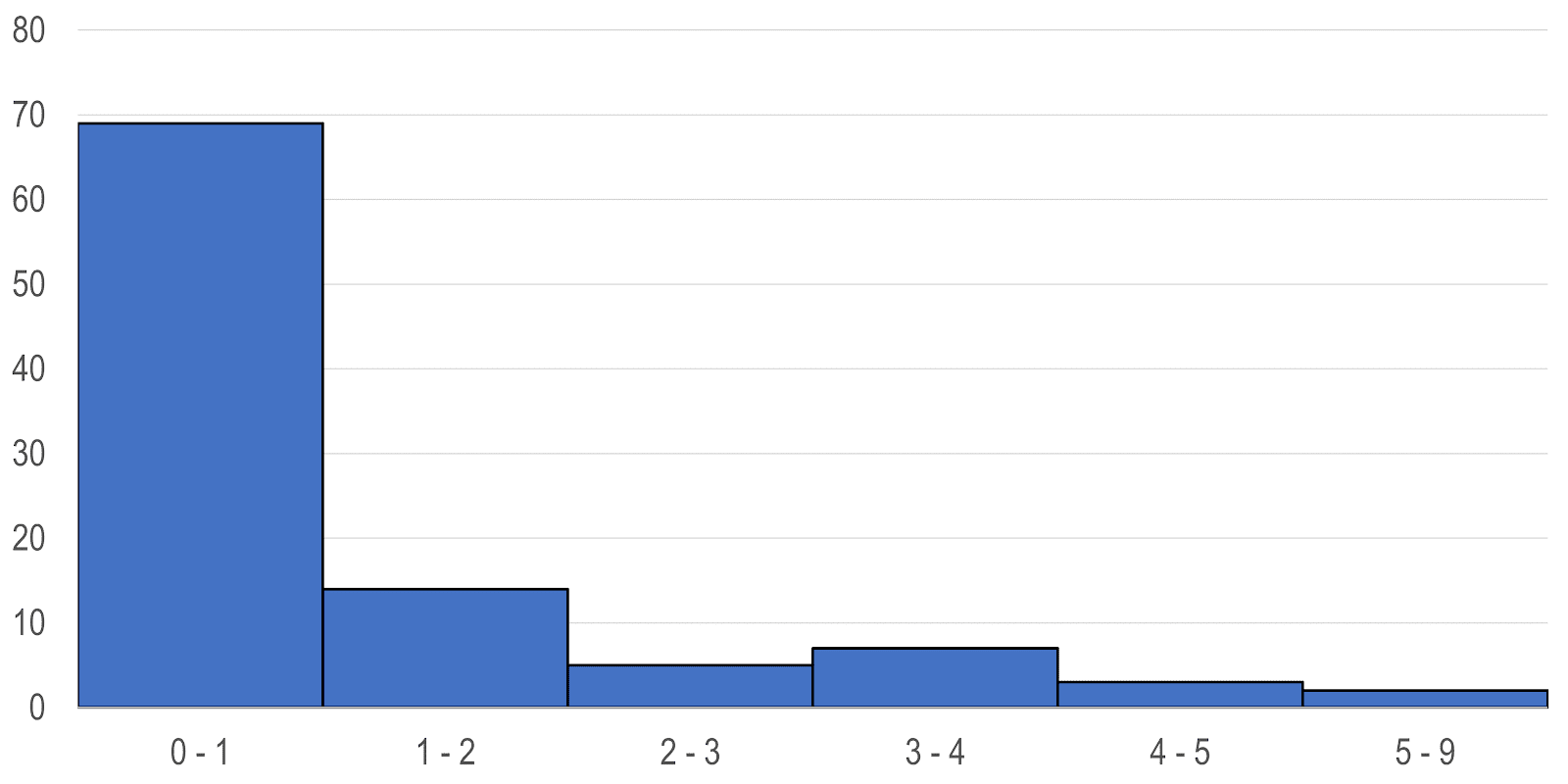
しかし、このように左右対称の山型分布にならないものも多くあります。分布が対称でないことを歪み skew があると表現し、 L型の分布と表現することがあります。そのうち峰が中央から左側に寄っていて、右側に長く裾を引く分布のことを、右に歪んだ分布、逆に峰が中央から右側に寄っているものを左に歪んだ分布といいます。こうしたL型の分布は、国民所得の分布や患者ごとの医療費の分布や医学・生物学における肝機能やホルモン値などの検査値などでよく見られます。
峰の数
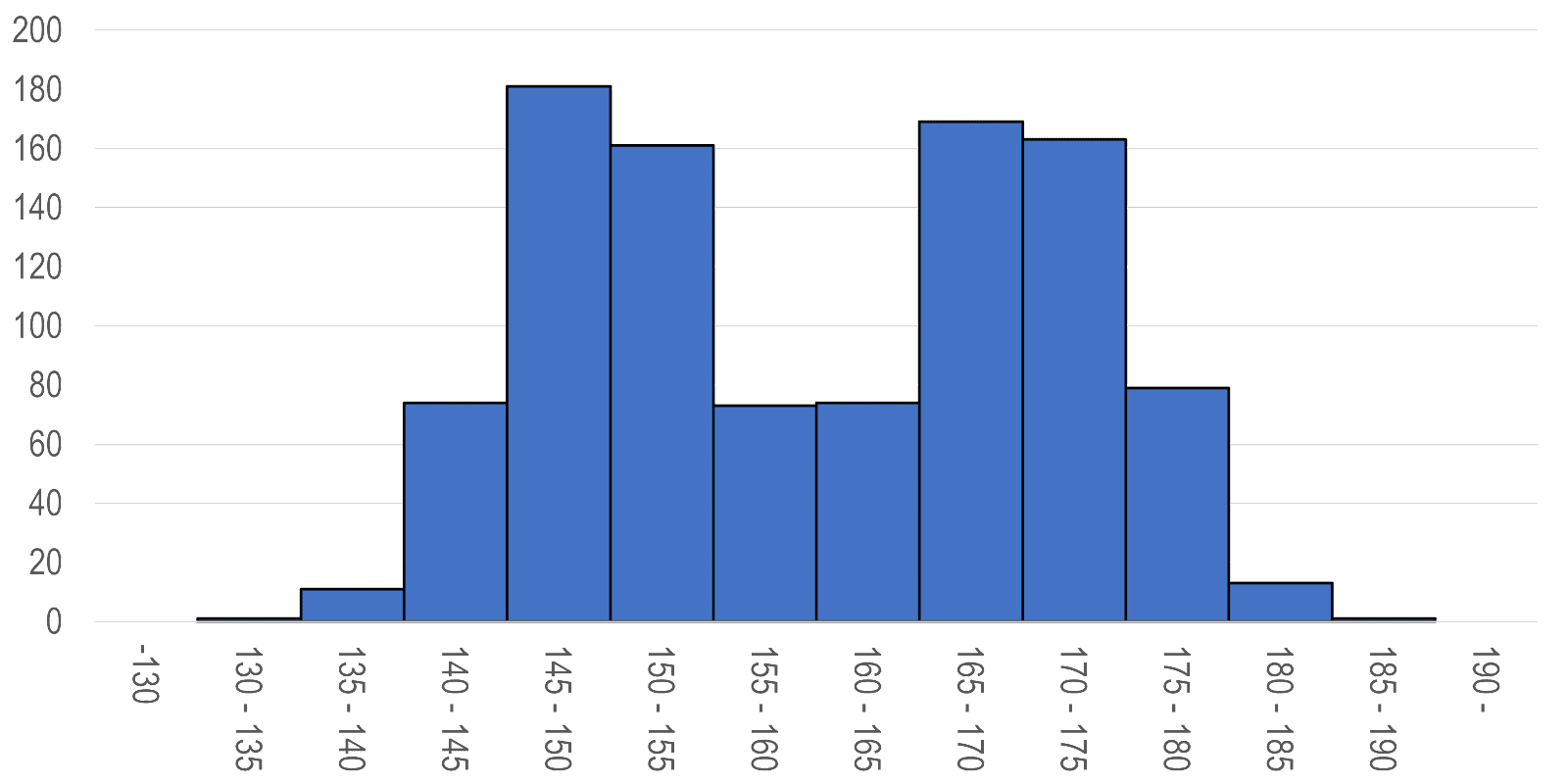
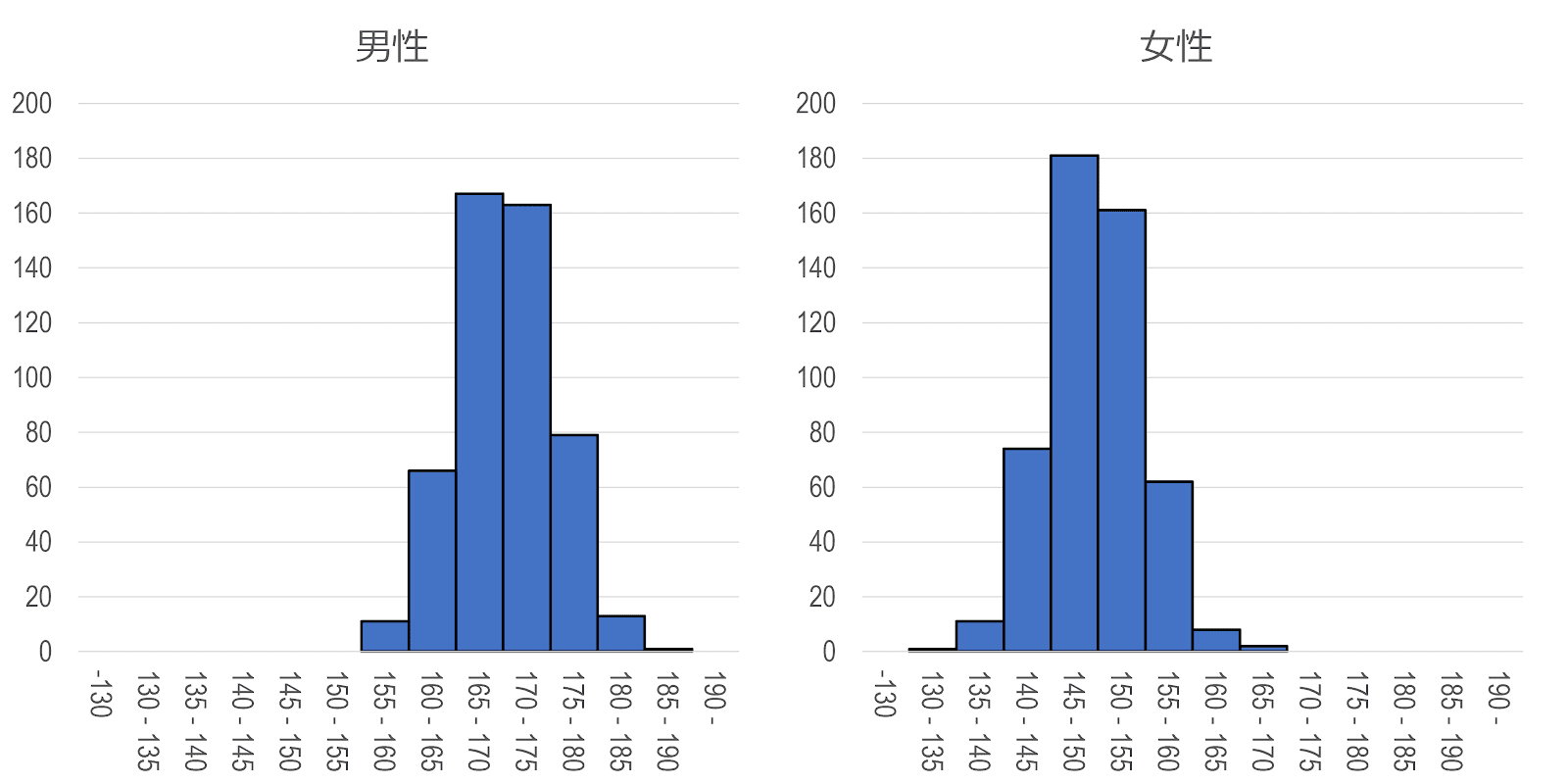
データによっては峰が2つ以上ある分布(双峰型 bimodal)も生じることがあります。そのような場合は、通常、性質の異なるデータが混じり合っていることが多く、適当にグループ分けすると、峰が1つの単純な分布が現れることがよくあります。このような操作を層別化といいます。たとえば、男女を区別しない集団の身長の分布は、しばしば2つの峰ができます。そのようなときには、性別による層別化を行います。
要約統計量
度数分布表やヒストグラムは、得られた情報をほぼすべて反映している表現形式ですが、別々の集団同士を比較する際には、少々複雑すぎて、比較がしにくいという問題もあります。そこで例えば、すべてのデータを1つの値に代表させ、その値で比較できれば、比較がしやすくなります。
一般に、データから求められる量(データの関数)を統計量 statistic といい、データ分布にみられる特性を要約的に表す統計量を要約統計量 summary statistics といいます。主な要約統計量には、代表値(分布の位置の指標)や散布度(分布のばらつきの指標)などがあります。
代表値
代表値 representative value とは、データ分布の中心的な位置を表すものです。度数分布やヒストグラムが人間の視覚能力による把握に依っているのに対し、代表値は数量的概念です。代表値の長所は、計算したり操作したり伝達するための客観性があることです。主な代表値には、平均値、中央値、パーセント点、最頻値があります$^\mathrm{(i)}$。
平均値
分布の位置の指標として最もよく用いられるのが平均値 means です。平均値というと、算術平均が最も有名ですが、そのほかにも幾何平均や調和平均というものもあります。
算術平均
算術平均 arithmetic mean は、最も有名な平均値であり、全観測値の合計を観測個数で割った値 \begin{gather} \bar{x}=\frac{1}{n}\sum_{i=1}^{n}x_i \end{gather} で定義されます。
例えば、表2の試験成績の場合、 \begin{gather} \bar{x}=\frac{20+68+ \cdots +65}{100}=50.2 \end{gather} となります。 このように、分子がデータの単純な合計である場合を、単純算術平均 simple arithmetic mean と呼びます。
観測値が連続的なデータの場合、あるいは離散的データであっても、試験の得点のように、とりうる値がかなり多い場合には、この公式を直接用います。しかし、そうではなくて、離散的なデータであって、同じ観測値をとる個体が複数存在する場合には、各観測値に対してその値をとる度数をかけて、その合計をデータの大きさで割ります。たとえば500人に対してある1日にとった食事の回数を聞いたところ、表3のような結果になったとすると、平均食事回数は \begin{gather} {\bar{x}}_w=\frac{43\times1+179\times2+238\times3+38\times4+2\times5}{43+179+238+38+2}=2.554 \end{gather} となります。
| 食事回数 | 人数 |
|---|---|
| $1$ | $43$ |
| $2$ | $179$ |
| $3$ | $238$ |
| $4$ | $38$ |
| $5$ | $2$ |
一般に観測値のとりうる値を $w_1,w_2, \cdots ,w_k$ とし、それぞれの度数が $x_1,x_2, \cdots ,x_k$ であるとすると、平均は \begin{gather} {\bar{x}}_w=\frac{\sum_{i=1}^{n}{w_ix_i}}{\sum_{i=1}^{n}w_i}=\frac{w_1x_1+w_2x_2+ \cdots +w_kx_k}{w_1+w_2+ \cdots +w_k} \end{gather} によって求めることができます。 このように、分子がデータの重みをつけた合計である場合を、加重算術平均 weighted arithmetic mean と呼びます。
幾何平均
幾何平均 geometric mean、あるいは相乗平均とは、観測値の積の累乗根 \begin{gather} {\bar{x}}_{\mathrm{G}}= \left(\prod_{i=1}^{n}x_i\right)^\frac{1}{n}=\sqrt[n]{x_1 \cdot x_2 \cdots x_n} \end{gather} で定義されます。
ここで、両辺の対数をとると、 \begin{gather} \log{{\bar{x}}_{\mathrm{G}}}=\frac{1}{n}\sum_{i=1}^{n}\log{x_i}=\bar{Z}\\ {\bar{x}}_{\mathrm{G}}=e^{\bar{Z}} \end{gather} つまり、幾何平均は、対数変換後のデータの算術平均を取り、それをもとのスケールに戻した(対数の逆関数である指数関数をとった)値ともいえます。
例えば、ある土地の地価が5年間の間にそれぞれ、21.8%、30.5%、53.6%、50.0%、12.9%上昇したとき、この5年間の年平均上昇率は、 \begin{gather} \bar{x}=\frac{21.8+30.5+53.6+50.0+12.9}{5}=33.8\% \end{gather} ではなく、幾何平均を用いなければなりません。 すなわち、 \begin{gather} {\bar{x}}_{\mathrm{G}}=\sqrt[5]{1.218 \cdot 1.305 \cdot 1.536 \cdot 1.500 \cdot 1.129}=1.328 \end{gather} となり、32.8%が平均上昇率です。
幾何平均は、母集団が対数正規分布に従う場合(具体的には、右に歪んだ分布)、適切な代表値とされています。
調和平均
調和平均 harmonic mean は、「逆数の算術平均」の逆数 \begin{gather} {\bar{x}}_{\mathrm{H}}=\frac{n}{\sum_{i=1}^{n}\frac{1}{x_i}}=\frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+ \cdots +\frac{1}{x_n}} \end{gather} で定義されます。
例えば、ある路線バスが行きは時速25 km、帰りは時速15 km で往復したとすると、その平均時速は \begin{gather} \bar{x}=\frac{25+15}{2}=20 \end{gather} ではありません。 路線の距離を $d$ とすると、往復距離 $2d$ を時間で割って平均時速 $v$ は \begin{gather} v=\frac{2d}{\frac{d}{25}+\frac{d}{15}}=\frac{1}{\frac{1}{2} \left(\frac{1}{25}+\frac{1}{15}\right)}=18.75 \end{gather} となります。
中央値
例えば、 \begin{align} \boldsymbol{x}= \left\{1,\ 1,\ 1,\ 1,\ 2,\ 3,\ 4,\ 5,\ 16,\ 20\right\} \end{align} というデータがあった場合、 平均は、 \begin{gather} \bar{x}=\frac{1+1+1+1+2+3+4+5+16+20}{10}=5.4 \end{gather} となりますが、 この値はこの分布を代表する値としてあまり良くありません。なぜなら、10個の観測値のうち、平均より小さいものが8個を占め、残りの2個が平均より大きいからです。分布の形が非対称でどちらかに歪んでいる場合、このようなことが起きます。度数は少ないけど値が大きいデータに平均が引っ張られている場合、平均値は分布の代表値として適当ではなく、例えば、所得分布は、ほとんどの場合分布が右に歪んでいて、ごくわずかな高所得者が平均値を押し上げていますが、それによって半数以上が「平均所得以下」になってしまいます。むしろ分布の中心という意味で、その値より小さな観測値の数と大きな観測値の数が等しくなるような値の方が望ましいといえます。そのような値を中央値といいます。
まず、観測値 $x_1,x_2, \cdots ,x_n$ を大きさの順序に並びかえたものを、小さいものから添え字にカッコをつけて \begin{gather} x_{ \left(1\right)} \lt x_{ \left(2\right)} \lt \cdots \lt x_{ \left(n\right)} \end{gather} と書き、 これを順序統計量 order statistics と呼びます。
中央値 median(または、中位数)は、観測値を小さいもの(大きいものでもよい)から順番に並びかえたときの、中央の値であり、 \begin{gather} \mathrm{Median}= \left\{\begin{matrix}x_{ \left(m+1\right)}&n=2m+1\\\frac{x_{ \left(m\right)}+x_{ \left(m+1\right)}}{2}&n=2m\\\end{matrix}\right. \end{gather} で定義されます。
例えば、先ほどのデータの中央値は、 \begin{gather} \mathrm{Median}=\frac{2+3}{2}=2.5 \end{gather} となります。
中央値を求める際に用いるのは、各データの全体の中での「順」位のみです。実際の数値がいくつなのかは、問題になりません。例えば、$ \left\{8,10,12,14,16\right\}$ というデータと、$ \left\{8,10,12,14,100\right\}$ というデータがあった時、平均値の場合は前者が12.0、後者が38.8と、外れ値100の影響を強く受けます。しかし中央値ならば、16であろうが100であろうが「一番大きな数字」という情報のみが残りますので、結局どちらのデータでも中央値は12(上からも下からも3番目の順位)になります。数値自体の情報が失われてしまう反面、わずかな外れ値に全体が引きずられてしまうようなことは起こりにくくなります。
パーセント点
中央値の考え方を拡張したものに分位点があります。観測値を小さいものの順に並びかえたとき、小さい方から$100p\% \left(0 \le p \le 1\right)$の所にある値を $100p$ パーセント点 percentile、または(百)分位点といいます。
よく用いられる分位点には四分位点 quartile があります。これは、小さいもの順に並びかえられたデータを4等分したときの3つの分割点であり、第1四分位点 $Q_1$ は25%分位点、第2四分位点 $Q_2$ は50%分位点(すなわち中央値)、第3四分位点 $Q_3$ は75%分位点です。(分位点がデータとデータの間におちる場合には、中央値と同様、その2つのデータの平均を分位点とします)。また、分布全体の位置を把握する目的で、2.5%点と97.5%点もしばしば用いられます。
最頻値
平均値、中央値の他によく用いられる分布の代表値には、最頻値があります。最頻値 mode とは、最も多く観測された値、つまり分布の峰に対応する値のことです。度数分布表においては、その度数が最大である階級の階級値が最頻値となります。
例えば、先のデータ $ \left\{1,\ 1,\ 1,\ 1,\ 2,\ 3,\ 4,\ 5,\ 16,\ 20\right\}$ の場合、4回観測されている1が最頻値となります。
中央値と同じように、最頻値も、外れ値に強い代表値で、中央値が「データの順位」だけを気にしていたのと同様に、最頻値は「データの個数」のみに着目しています。ただ、峰が2つ以上ある分布の場合には、有効な代表値とはいえず、最頻値が連続データに対して実際に使われることは稀にしかありません。
平均値・中央値・最頻値の大小関係
平均値、中央値、最頻値の大小関係について、峰が1つある単峰性の分布で、分布が完全に左右対称(正規分布)の場合、この3つは完全に一致します。したがって、ほぼ左右対称の分布の場合にはどの代表値を用いてもさほど差がありません。分布が左右対称ではなくて、峰が中心より左側に寄っている場合、いいかえると右側の裾が長い分布(つまり右に歪んだ分布)では、一般的に平均値、中央値、最頻値の順に \begin{gather} \mathrm{Mean} \gt \mathrm{Median} \gt \mathrm{Mode} \end{gather} となります。
逆に左に歪んだ分布の場合には、 \begin{gather} \mathrm{Mean} \lt \mathrm{Median} \lt \mathrm{Mode} \end{gather} となります。
適切な代表値
こうした3つの代表値のうち、平均値と中央値がよく使われています。特に、平均値は最も普通の統計解析と密接に結びついているので非常によく使われますが、中央値も記述統計量としては何も劣るところはなく、分布が左右どちらかに歪んでいる場合、中央値の方が適切な指標となります。
また、中央値は、分布が左右対称な場合、平均値とほぼ同じ値になるので、使用するにあたっての仮定や前提が少なく、状況をあまり選ばない(ほとんどいつでも妥当性が高い)という意味で、中央値は最も使い勝手が良い代表値と評価することもできます。
散布度
ただ、得られたデータを要約するために、代表値だけを使えばそれで十分かというと必ずしもそうとは限りません。例えば、大きさが同じ $n=10$ の3つのデータ $\boldsymbol{A},\boldsymbol{B},\boldsymbol{C}$ があったとします(例えば、10点満点の小テストを10人のクラス3つで行ったときの結果)。 \begin{align} \boldsymbol{A}= \left\{0,\ 3,\ 3,\ 5,\ 5,\ 5,\ 5,\ 7,\ 7,\ 10\right\}\\ \boldsymbol{B}= \left\{0,\ 1,\ 2,\ 3,\ 5,\ 5,\ 7,\ 8,\ 9,\ 10\right\}\\ \boldsymbol{C}= \left\{3,\ 4,\ 4,\ 5,\ 5,\ 5,\ 5,\ 6,\ 6,\ 7\right\}\\ \end{align}
これら3つの平均値、中央値、最頻値はいずれも5ですが、分布は異なっており、当然、同じデータとはいえません。$\boldsymbol{A},\boldsymbol{B}$ と $\boldsymbol{C}$ では分布の最小値と最大値が異なります。$\boldsymbol{C}$ は $\boldsymbol{A},\boldsymbol{B}$ に比べると、かたまって分布しているからです。$\boldsymbol{A}$ と $\boldsymbol{B}$ は分布の範囲は同じですが、度数分布のグラフを書くと、山の尖り方が異なり、$\boldsymbol{A}$ の方が尖っています。この $\boldsymbol{A},\boldsymbol{B},\boldsymbol{C}$ 3つの分布は、なめらかな分布を想定すると図2.17のような関係になっています。このことから、代表値は分布の位置を示す指標であって、この例のような $\boldsymbol{A},\boldsymbol{B},\boldsymbol{C}$ 3つの分布を区別するには、分布の形状を示す他の指標が必要となることが分かります。
このように、個体による点数の差の程度を全体的に考えたものを点数の散布度 dispersion、分散度、ちらばり、ばらつきなどと呼びます。主な散布度を表す指標に、範囲、四分位範囲、標準偏差、変動係数があります。
範囲
最も単純な散布度の指標が範囲です。範囲 range とは、データの最大値と最小値の差であり、 \begin{gather} \mathrm{R}=x_{max}-x_{min} \end{gather} で定義されます。
つまり分布の端から端までの距離のことです。前の3つの分布 $\boldsymbol{A},\boldsymbol{B},\boldsymbol{C}$ では、 \begin{gather} {\mathrm{R}}_A={\mathrm{R}}_B=10\\ {\mathrm{R}}_C=4 \end{gather} となり、 $\boldsymbol{C}$ は $\boldsymbol{A},\boldsymbol{B}$ と比較してかたまって分布していることが分かります。
範囲は散布度の尺度としてはかなり粗いものです。たとえば、${\mathrm{R}}_A={\mathrm{R}}_B$ ではありますが、両者の分布は異なっており、分布の違いを記述することはできません。
また、範囲は最大値、最小値のみに依存するので、データの中に極端に大きい(小さい)外れ値が存在するような場合、これに大きく左右されます。このような理由から、範囲は特殊な場合を除いて、あまり用いられることはありません。
四分位範囲
範囲を改良したものに、四分位範囲があります。四分位範囲 inter-quartile range とは、データの第3四分位点の値と第1四分位点の値の差であり、 \begin{gather} \mathrm{IQR}=Q_3-Q_1 \end{gather} で定義されます。
また、第3四分位点と第1四分位点の隔たりの半分を四分位偏差 quartile deviation, semi-interquartile range といい、 \begin{gather} \mathrm{QD}=\frac{1}{2} \left(Q_3-Q_1\right) \end{gather} で定義されます。
四分位範囲は、データの半数が含まれている範囲のうち、ちょうど真ん中にあるもの、四分位偏差はその平均を意味します。四分位範囲が狭いほど、まとまった分布となり、広いほど、散らばった分布となります。四分位範囲や四分位偏差は、両側 $\frac{1}{4}$ のデータを考慮しないため、外れ値の影響を受けにくくなっています。
分散・標準偏差
範囲も四分位範囲も、与えられた観測値の散らばり具合を表現するのに、たかだか2個ないし4個の観測値を用いるだけであり、すべての観測値を用いていません。この点、すべての観測値のもつ情報を利用した散らばりの尺度が分散や標準偏差です。
いま、試験成績の例で考えると、すべての人の点数にあまり大きな差がないとすれば、各人の点数は、みな平均点に近いものとなるでしょう。これに対して、人によって点数に大きな差があるときには、平均点から大きく離れた点数の人もいます。そこで、各人の点数の平均点からのズレを考え、その平均的な大きさによって、点数の散布度を測ることができると思われます。
偏差
この各観測値と平均値との差(ズレ)のことを偏差 deviation と呼びます。単純に考えれば、この偏差の平均を取ればよさそうですが、以下に示すように、偏差の合計は、常に0となり、尺度としては使えません。 \begin{align} \sum_{i=1}^{n} \left(x_i-\bar{x}\right)&= \left(x_1-\bar{x}\right)+ \left(x_2-\bar{x}\right)+ \cdots + \left(x_n-\bar{x}\right)\\ &= \left(x_1+x_2+ \cdots +x_n\right)-n\bar{x}\\ &= \left(x_1+x_2+ \cdots +x_n\right)-n \cdot \frac{1}{n} \left(x_1+x_2+ \cdots +x_n\right)\\ &=0 \end{align}
平均絶対偏差
これは、偏差には、正の値を取るものもあれば、負の値を取るものもあり、それらが打ち消しあうことに起因します。そこで次に、偏差の絶対値をとり、その算術平均を散布度の尺度とすることを考えます。これを平均絶対偏差 average absolute deviation と呼びます。 \begin{gather} \mathrm{AAD}=\frac{1}{n}\sum_{i=1}^{n} \left|x_i-\bar{x}\right| \end{gather}
分散
平均絶対偏差は、最も単純で分かりやすい尺度ですが、絶対値を含むかたちだと、計算やデータを整理する際に少々不便なので、同様に「平均値からの距離」を表すために、偏差を2乗したものの平均を考えます。 \begin{gather} S^2=\frac{1}{n}\sum_{i=1}^{n} \left(x_i-\bar{x}\right)^2 \end{gather} これを分散 variance と呼びます。分散は、2乗値の和であるため必ず0以上の値となり、ばらつきの大きなデータならば大きい値に、小さいデータならば小さな値になります。
標準偏差
取ったデータの散布度を比較するだけであれば、分散をそのまま用いて比較することができます。ただ、1点注意すべきことがあります。それは、偏差を2乗しているため、単位もそのまま2乗されてしまっているということです。例えば、身長データの場合、分散の単位は $\mathrm{m^2}$ であり、「長さ」の尺度ではなく、「面積」の尺度のようにも見えてしまいます。このため、分散の正の平方根を取ることで、データの単位を元に戻す必要があります。 \begin{gather} S=\sqrt{S^2} \end{gather} これを、標準偏差 standard deviation と呼びます。標準偏差は、扱っているデータと単位がそろっているので、データのばらつきを記述する際には、分散よりも標準偏差の方がよく用いられます。
変動係数
標準偏差は、データのばらつきを要約する指標ですが、性質が異なるもの同士だと、ばらつき度合いを比較するのが難しい場合があります。
例えば、ある10人の身長〔m〕と体重〔kg〕のデータが次のように得られたとします。 \begin{gather} \mathrm{Height}= \left\{170.0,\ 158.6,\ 151.0,\ 150.2,\ 151.9,\ 146.5,\ 143.8,\ 166.7,\ 152.3,\ 151.7\right\}\\ \mathrm{Weight}= \left\{48.3,\ 50.8,\ 50.1,\ 51.7,\ 43.9,\ 54.3,\ 47.7,\ 48.5,\ 44.4,\ 47.4\right\} \end{gather}
ここから標準偏差を計算すると、 \begin{gather} S_H\cong7.96 \left[\mathrm{m}\right] \quad S_W\cong3.00 \left[\mathrm{kg}\right] \end{gather} となります。 しかし、これを比較しようにも、単位が違うので横並びの比較をすることができません。
また、例えば、ある個人商店 $\boldsymbol{A}$ とスーパー $\boldsymbol{B}$ の10日間の売り上げデータ(単位:万円)が次のように得られたとします。 \begin{gather} \boldsymbol{A}= \left\{5,\ 3,\ 6,\ 8,\ 9,\ 8,\ 10,\ 2,\ 7,\ 4\right\}\\ \boldsymbol{B}= \left\{87,\ 32,\ 96,\ 77,\ 52,\ 26,\ 93,\ 87,\ 47,\ 70\right\} \end{gather}
ここから標準偏差を計算すると、 \begin{gather} S_A=2.52 \quad S_B=24.41 \end{gather} となります。 しかし、この2つの値を比較して「スーパーの方が個人商店よりも変動性が大きい」と結論することはできません。なぜなら、個人商店の方がスーパーよりも小さな値を取っているので、値そのものを比較しようとすると、大きな値を取る方が不利になってしまうからです。
標準偏差は、データの散らばりを絶対的な大きさで示したものですが、データの平均的な大きさが大きければ、その散らばりの絶対的な大きさも、通常、大きくなります。したがって、このような場合に、データの平均との相対的関係を考えた尺度を用いる必要があります。これを変動係数と呼びます。
変動係数 coefficient of variation とは、平均値に対する標準偏差の比として、 \begin{gather} \mathrm{CV}=\frac{S}{\bar{x}} \end{gather} で定義されます。
平均と標準偏差は同じ単位をもつため、その比である変動係数には単位がありません。そのため変動係数は、異なる単位をもつ項目間や同じ単位ではあるけど桁が違うような集団など、直接の比較が困難な場合に、バラツキの大きさを相対的に比較する際、便利な指標です。
分布の形状ごとの適切な要約の仕方
データの記述の本質は、情報を要約することにありますが、要約が適切であるためには、いくつかの前提が必要となります。多くの調査や研究では、平均と標準偏差が要約統計量として使われていますが、これらが適切であるためには「分布の形状が左右対称で、山が1つだけ」(より詳細には、分布が正規分布である程度近似できること)という仮定が必要です。
いっぽう、中央値について説明した際にも述べたように、外れ値がある場合や分布に歪みがある場合、データの個数が少ないときなどには、平均と標準偏差を用いることはあまり妥当ではなくなってしまいます$^\mathrm{(ii)}$。特に、社会科学における所得の分布や医学・生物学における生体データなどは、厳密に正規分布に従うデータは少なく、分布が歪んでいることがよくあります。分布が歪んでいる場合、何を代表値とするかについて、明確な基準があるわけではありませんが、パーセント点との関係から中央値と四分位範囲が用いられることが多いとされています。
前提からの乖離が大きい場合に不適切な要約を行えば、重要な情報を切り捨ててしまう危険につながります。捨て去る部分に重要な情報が隠れていないか、要約の前提を探索的に検討することが、適切な要約に必須となります。そのためには、グラフ表示など探索的データ解析手法を用い、分布の歪みや外れ値の存在を検討し、それらに対して頑健な要約統計量を用いる必要があります。
参考文献
- 東京大学教養学部統計学教室 編. 基礎統計学 1 統計学入門. 東京大学出版会, 1991, p.17-39
- ダグラス・アルトマン 著, 木船 義久, 佐久間 昭 訳. 医学研究における実用統計学. サイエンティスト社, 1999, p.17-39
- 宮川 公男 著. 基本統計学 第4版. 有斐閣, 2015, p.11-34, p.37-54
- 丹後 俊郎, 松井 茂之 編集. 医学統計学ハンドブック 新版. 朝倉書店, 2018, p.20-41
- 五十嵐 中. わかりませんから始める医療統計(03)「珍しさ」、どう測る?:伸び縮みするものさし・分散と標準偏差. 調剤と情報. 2014, 20(3), p.357-361
脚注
- このほか、例えば、「オリンピックでどの国が金メダルを取るか?」ということに関心がある場合、その国で最も成績が良い人のスコア、すなわち、「最大値」が代表値となることもあり得ます。
- 平均は外れ値の影響を強く受けますが、標準偏差は大きな偏差を2乗するので影響がいっそう大きくなります。



0 件のコメント:
コメントを投稿