コホート研究は、医学・疫学研究において最もよく実施されて基本的な研究デザインです。本稿では、閉鎖コホートと開放コホート、リスク集団、コホート研究のデータの取り方、評価指標(発生割合・発生率)の定義、長所と短所などについて解説しています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
- 曝露(発症)状況を表す右下の添え字は、「0」である場合($n_0,\pi_0$ など)や「2」である場合($n_2,\pi_2$ など)がありますが、どちらも「非曝露群(コントロール群)」を表しています。
コホート研究の進め方
コホートとは?
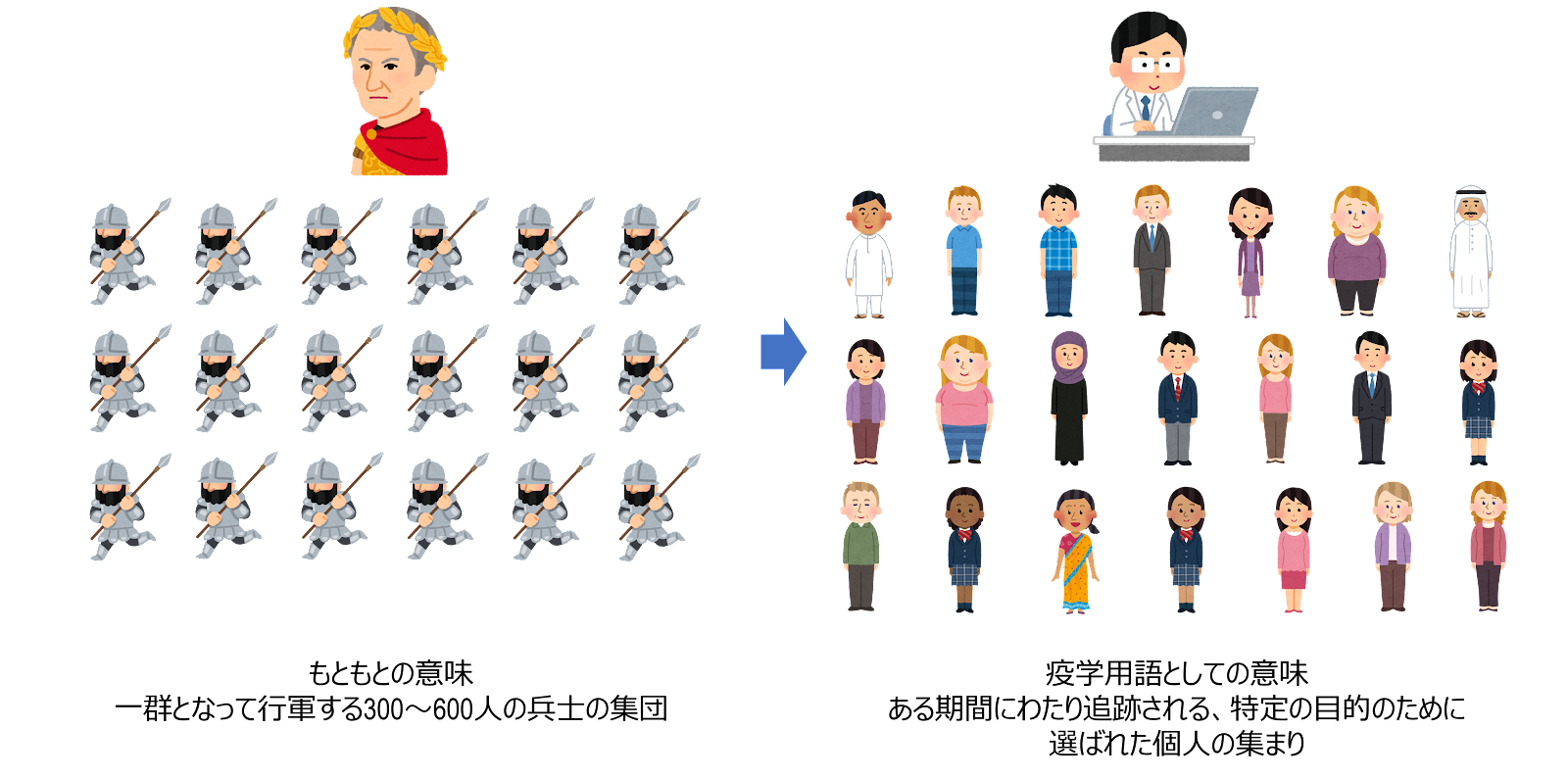
コホート cohort とは、もともと古代ローマにおいて、「一群となって行軍する300~600人の兵士の集団」を意味する言葉であり、医学・疫学の用語としては、ある期間にわたり追跡される、特定の目的のために選ばれた個人の集まりと定義されます。
観察手順の概要
コホート研究は、前向き・後ろ向きどちらでも実施することは可能ですが、基本的には前向きに行われ、観察の方向性は、「曝露」→「疾病発生」という順行 forward の向きです。コホート研究はこのような疾病の自然史に沿って観察を行う方法であり、ケース・コントロール研究と比較すると素直な研究方法と言えます。
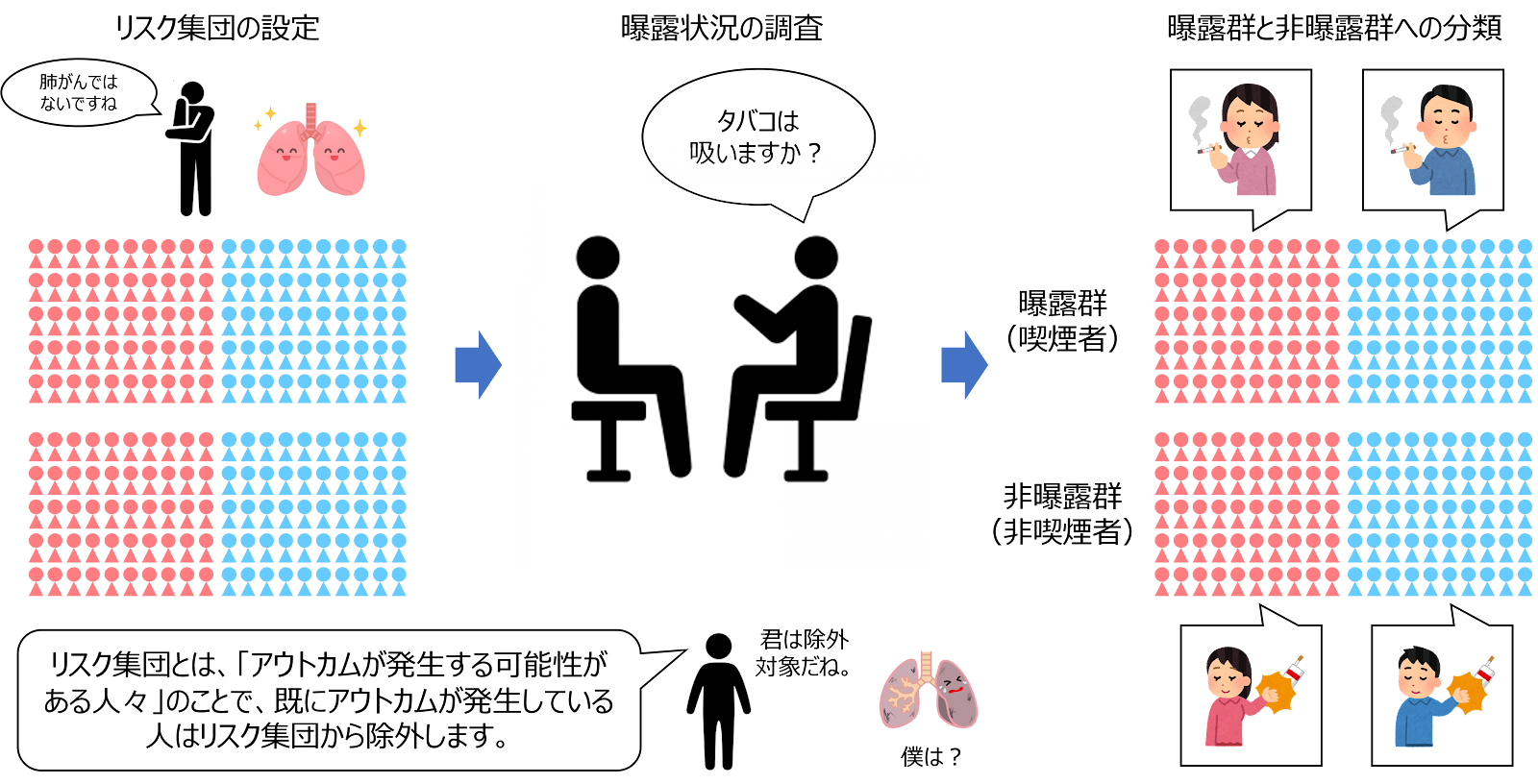
前向きコホート研究 prospective cohort study では、まず研究対象となるリスク集団を設定し、観察開始(ベースライン)時点に、各対象者について、関心のある危険因子への暴露状況を測定し、曝露群 exposed と非曝露群 unexposed に分けます。なおこのとき、仮説検証を行うアウトカムやその危険因子は、1つだけでなく、複数設定することができます。
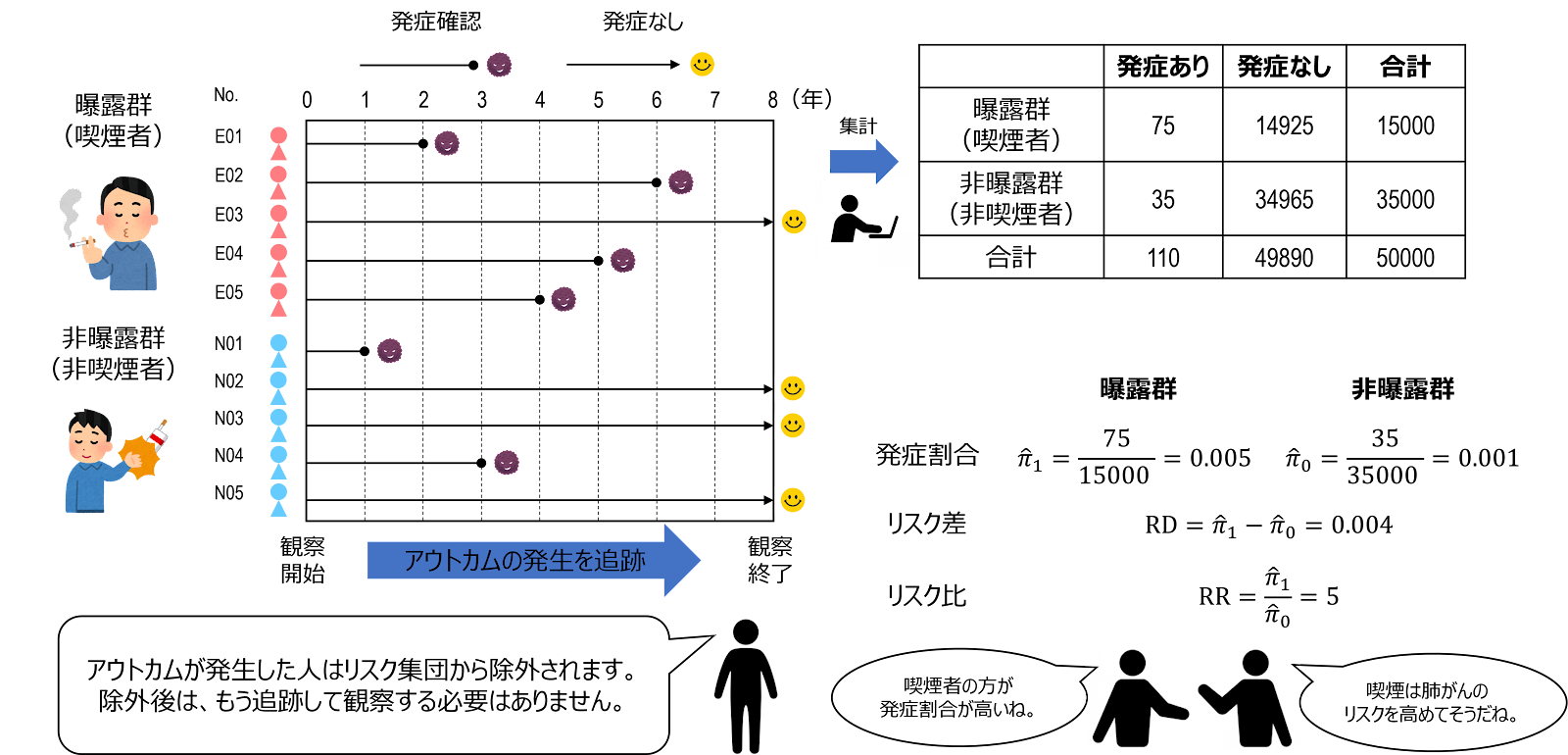
その後、予定している観察期間が終わるまで、コホートを追跡(定期的にアウトカムの発生状況を測定)し、それぞれの群で新規にアウトカムを発生した人の数をカウントしていきます。
最後に、集めたデータから発生割合や発生率を算出し、リスク比やリスク差によって、両群の比較を行います。
リスク集団
前向きコホート研究の第1歩は、研究対象となる「リスク集団」を設定することです。リスク集団 population at risk とは、アウトカムが発生する可能性(リスク)を有している人々のことで、リスク集団の一員としてカウントされるための標準的な必要条件は、観察開始(ベースライン)時点で既にアウトカムが発生していないという条件です。
例えば、「喫煙は肺がんの危険因子か?」ということを調べたい場合、既に肺がんになっている人を観察しても、改めて肺がんを発生することはなく、因果関係を推測するうえで価値のある情報は得られません。
また、仮に肺がん患者を含めて喫煙状況の観察をスタートし、最終的に「非喫煙者の方が肺がんとなった人が多い」という結果が得られたとします。この場合、たしかに「喫煙が肺がん発生のリスクを抑えた」と解釈することも可能ですが、「肺がんを発生し、喫煙に苦しさしか感じなくなったので喫煙を止めた」という可能性もあり得ます。この場合、「曝露が疾病の原因になっている」のではなく、「アウトカムが発生したことによって曝露が生じた」ということになりますが、いずれにしても、有効な因果推論の妨げとなってしまいます。
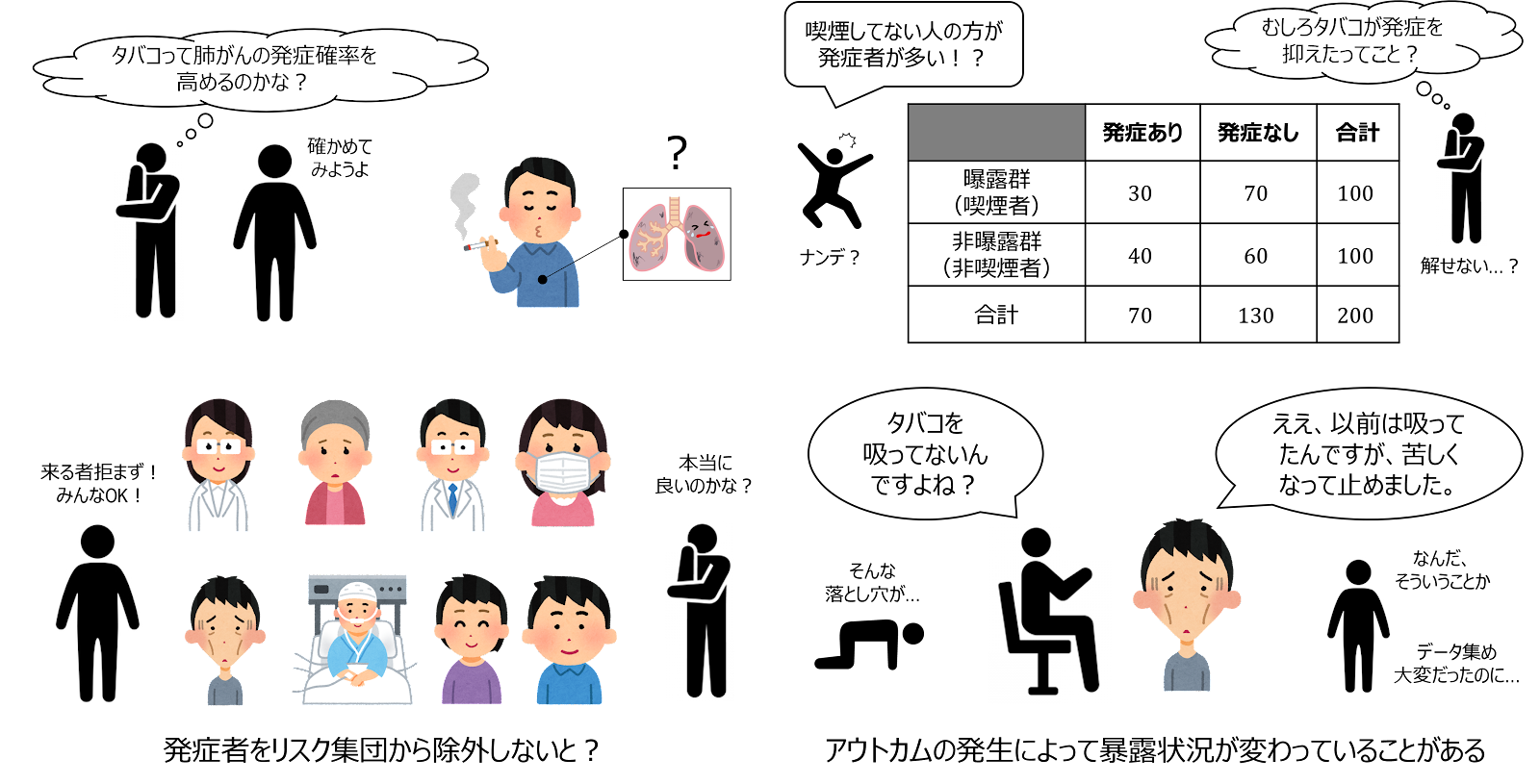
こうしたことから、「観察開始(ベースライン)時点で既にアウトカムが発生していない」という条件にもとづいて、対象とする集団を設定します。また、特に、発生が1度しかないアウトカム(死亡や発がんなど)の場合、コホート内の病気を発生した人はもう二度とリスクにさらされることはないので、アウトカムが発生したらすぐにリスク集団から除外します。同様に、一般的に追跡期問中に死亡した人は、(死因を問わず)「アウトカムが発生する可能性がある人」ではなくなるため、リスク集団から除外します。
リスク集団から除外された人に関しては、その後、観察を続ける必要はありません。
閉鎖コホートと開放コホート
コホート研究において追跡調査するコホートには、閉鎖コホート closed cohort と開放コホート open cohort の2種類があります。
閉鎖コホートとは、メンバーが固定されているコホートのことで、一度、対象者が設定され、追跡が始まると、誰も閉鎖コホートに加わることはできません。当初の登録対象者は、死亡や追跡不能、疾病を発生したりするなどして、しだいに数が少なくなっていきます。閉鎖コホートとした場合、発生割合と発生率の両方を算出することができます。有名なフラミンガム心臓研究 Framingham Heart Study は、1949年に始まった閉鎖コホートの例です。
いっぽう、開放コホートは、動的コホート dynamic cohort や動的集団 dynamic population ともいわれ、時間経過とともに新しいメンバーの受け入れを行います。そのため、観察対象者は、研究期間中にしばしば増減します。開放コホートとした場合、個人ごとに観察開始時期が異なり、発生割合を求める対象期間のスタート地点をどこにすればいいか、はっきり決められないため、発生率のみを求めることができます。しばしば行われているがん登録調査が、開放コホートの例です。

データの形式と基本指標①:発生割合
分割表の形式①
前向きコホート研究の分割表は、横断研究の場合と同様の形式で、一般に、ある観察期間が完了した時点における、各群の新規発生者数を、以下のような $2\times2$ 分割表にまとめます。
| 発生あり $ \left(D\right)$ | 発生なし $(\bar{D})$ | 合計 | |
|---|---|---|---|
| 曝露群 $ \left(E\right)$ | $a$ | $c$ | $n_1$ |
| 非曝露群 $(\bar{E})$ | $b$ | $d$ | $n_0$ |
| 合計 | $m_1$ | $m_0$ | $N$ |
発生割合
閉鎖コホートを用いるコホート研究では、曝露群と非曝露群の発生割合をそれぞれ \begin{gather} {\hat{\pi}}_1 \quad {\hat{\pi}}_0 \end{gather} とすると、 推定値は、次のように定義されます。
\begin{gather} {\hat{\pi}}_1=\frac{a}{n_1} \quad {\hat{\pi}}_0=\frac{b}{n_0} \end{gather}
曝露と疾病の関係性の評価①:発生割合
曝露効果の評価指標である、リスク差やリスク比は、それぞれ、以下のように定義されます。なお、リスク比について、「非曝露群のリスクを分母、曝露群のリスクを分子」とするのが標準的だと思われますが、どちらを分母・分子とするかは、研究者が自由に設定することができます。同様に、差の場合も、どちらを引く数・引かれる数にするかは研究者の自由です。
発生割合差:発生リスク差
\begin{gather} \mathrm{\widehat{RD}}={\hat{\pi}}_1-{\hat{\pi}}_0=\frac{a}{n_1}-\frac{b}{n_0} \end{gather}
発生割合比:発生リスク比
\begin{gather} \mathrm{\widehat{RR}}=\frac{{\hat{\pi}}_1}{{\hat{\pi}}_0}=\frac{an_0}{bn_1} \end{gather}
データの形式と基本指標②:発生率
分割表の形式②
開放コホートの場合は、一般に、ある観察期間が完了した時点における、各群の観察時間と各群の新規発生者数を、以下のような $2\times2$ 分割表にまとめます。
| 新規発生数 $ \left(D\right)$ | 未発生数 $(\bar{D})$ | 合計 | 観察人・時 | |
|---|---|---|---|---|
| 曝露群 $ \left(E\right)$ | $a$ | $c$ | $n_1$ | $T_1$ |
| 非曝露群 $(\bar{E})$ | $b$ | $d$ | $n_0$ | $T_0$ |
| 合計 | $m_1$ | $m_0$ | $N$ | $T$ |
ただし、$t_i$ を曝露群の $i$ 番目の対象者の観察時間、$t_j$ を非曝露群の $j$ 番目の対象者の観察時間として、 \begin{gather} T_1=\sum_{i=1}^{n_1}t_i \quad T_0=\sum_{j=1}^{n_0}t_j\\ T=T_1+T_0 \end{gather} なお、このような方法による発生率の求め方は人年法と呼ばれます。
発生率
開放コホートを用いるコホート研究では、曝露群と非曝露群の発生率をそれぞれ \begin{gather} \mathrm{{\widehat{IR}}_1} \quad \mathrm{{\widehat{IR}}_0} \end{gather} とすると、 推定値は、次のように定義されます。
\begin{gather} \mathrm{{\widehat{IR}}_1}=\frac{a}{T_1} \quad \mathrm{{\widehat{IR}}_0}=\frac{b}{T_0} \end{gather}
曝露と疾病の関係性の評価②:発生率
発生割合のときと同様、リスク差やリスク比は、それぞれ、以下のように定義されます。
発生率差
\begin{gather} \mathrm{\widehat{IRD}}=\mathrm{{\widehat{IR}}_1}-\mathrm{{\widehat{IR}}_0}=\frac{a}{T_1}-\frac{b}{T_0} \end{gather}
発生率比
\begin{gather} \mathrm{\widehat{IRR}}=\frac{\mathrm{{\widehat{IR}}_1}}{\mathrm{{\widehat{IR}}_0}}=\frac{aT_0}{bT_1} \end{gather}
コホート研究の特徴
コホート研究は、横断研究やケース・コントロール研究と比較したとき、以下のような長所や短所があります。
長所①:比較や因果関係の推定がしやすい
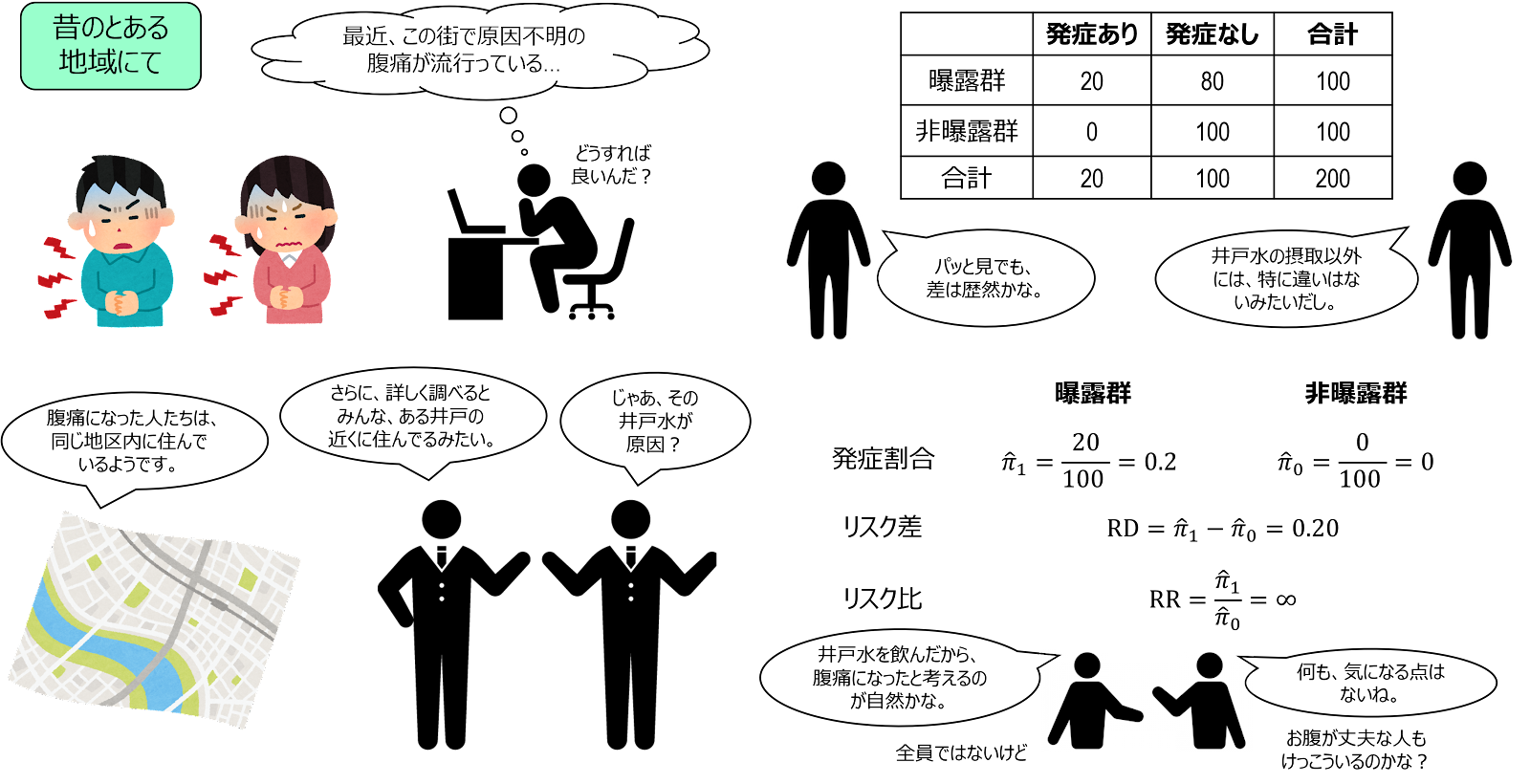
先述のように、前向きコホート研究は、「曝露」→「アウトカムの発生」という順序で事象が観察されるため、因果関係の推定がしやすい研究デザインです。また、発生割合や発生率が求められるため、群間の差や比による比較がしやすいという利点もあります。
ただし、コホート研究も含めた観察研究は、交絡などのバイアスによって誤った結論を導いてしまうこともあるので、因果推論の能力には限界があるという点には注意が必要です。
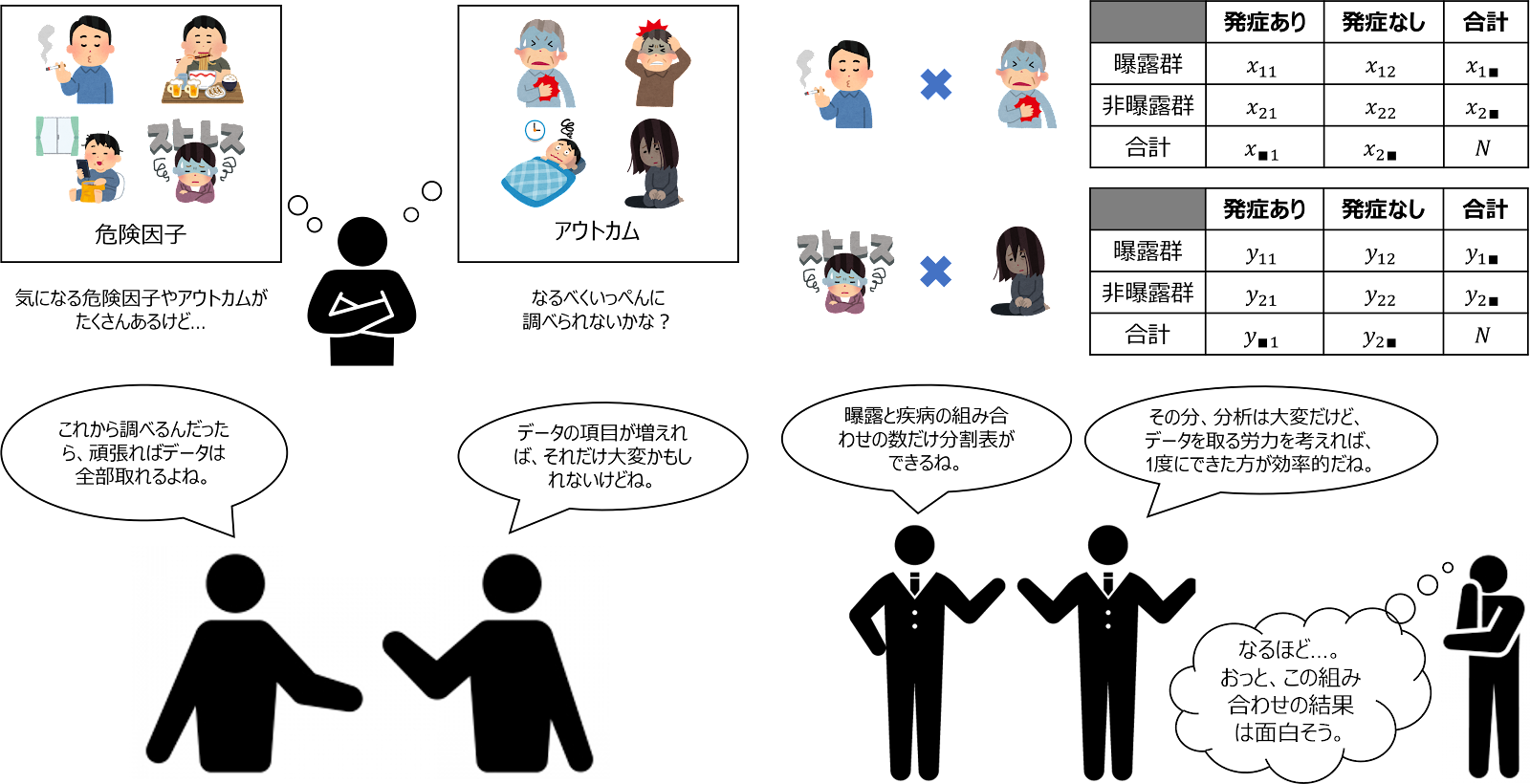
長所②:複数の曝露とアウトカムの関係を調べることができる
コホート研究は、前向きの実験デザインであるため、関心のある曝露やアウトカムに関するデータを意識的に集めることができます。この点、ケース・コントロール研究では、既に集められたデータしか利用できないため、調べたい因子の暴露状況に関するデータがない可能性もあり得ますが、コホート研究では、そうした心配はありません。かけられる手間や時間に応じて、複数の曝露とアウトカムに関するデータを取ることができます。
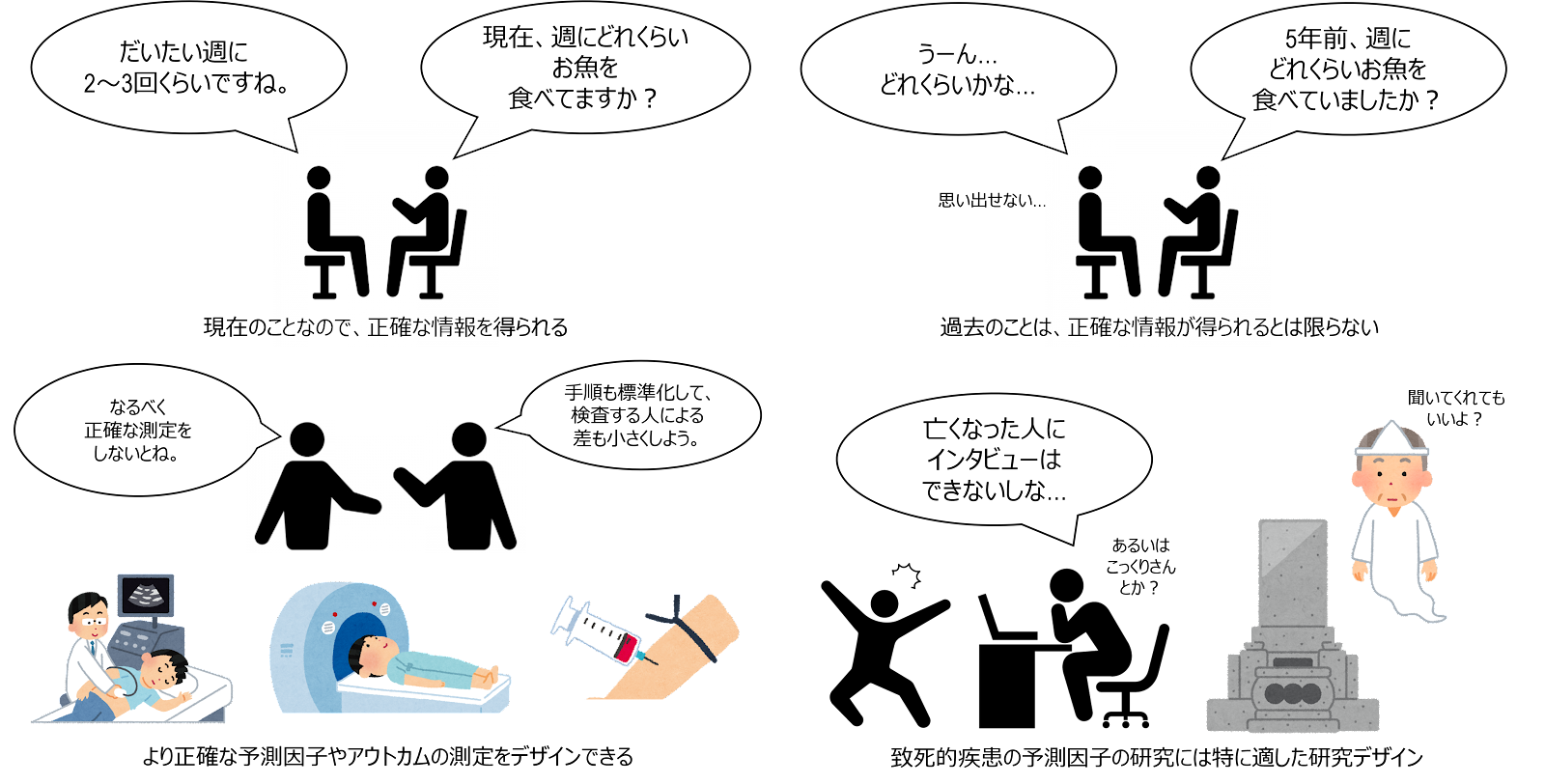
長所③:情報の正確性(データの妥当性)が高い
また、曝露の有無により曝露群と非曝露群に分類してから観察が始まるので、曝露情報については妥当性が高くなります。くわえて、アウトカム自体やアウトカムを知ったことによる予測因子への影響(例:肺がんに罹ったことを知ったために禁煙する)を避けることができる、後ろ向き研究に比べて、より完全で正確な予測因子やアウトカムの測定をデザインできるという利点もあります(後ろ向き研究では、すべてが測定済みであるため、研究者が測定の質をコントロールすることができません)。これは、食習慣のように、後から正確に思い出すことが難しいような因子の場合には、特に重要なメリットとなります。
さらに、前向きコホート研究は、致死的疾患の予測因子の研究には特に適した研究デザインです。このような研究を後ろ向き研究で実施しようとすると、研究者が入手しうる症例が偏ることがあり、また、本人はすでに死亡しているため、予測因子の情報を得るには、診療記録、友人、親類からの聞き取りなどに頼るしかなく、情報の正確性の担保に難点があります。
短所①:結果が得られるまでにコストがかかりやすい
コホート研究やケース・コントロール研究のどちらであっても、統計学的に信頼性のある結果を得るためには、ある程度のアウトカムの発生が観察されなければなりません。この点、前向きにデータを集めていくコホート研究は、アウトカムが発生するまで待機し、解析に耐え得るだけの量のデータが得られるまで待たなければなりません。このため、研究費用、時間、人手などのコストがかかりやすく、特に、発生割合(率)が非常に小さい稀な疾患とは相性が悪く、大規模な集団を長期間にわたり追跡調査することは、現実的には難しいこともあります。

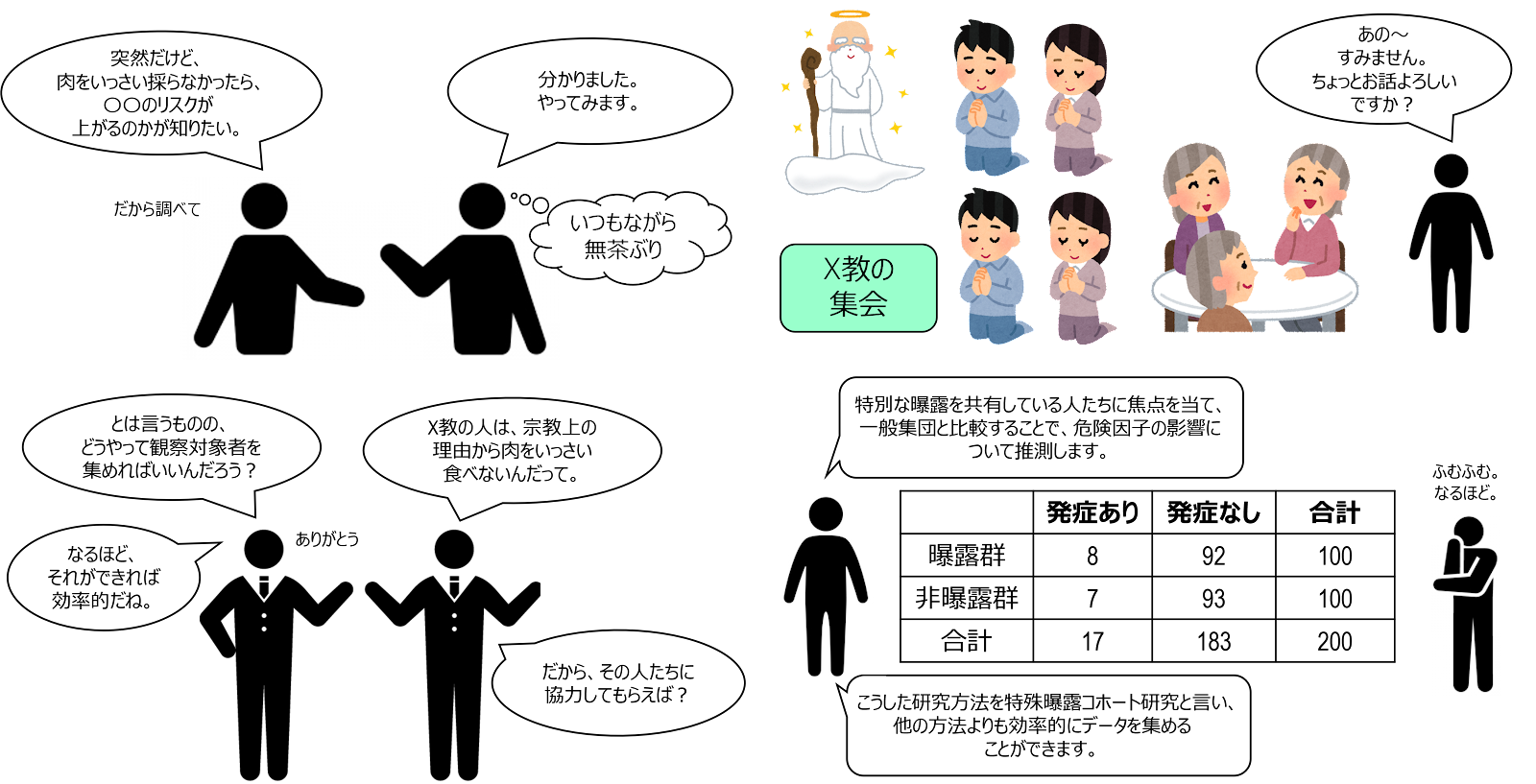
長所④:特殊(稀な)曝露に向いている
この点、例えば、「放射線物質の被ばくが健康に与える影響」など、危険因子に暴露される人が少ない(稀な)場合、一般集団の中から曝露群を設定することが難しい場合もあります。このような場合、コホート研究では、特別な曝露を共有している人(例えば、原子力発電所の職員)に焦点を当て、一般集団と比較するという方法を採ることができます。このようなコホート研究は、特殊曝露コホート研究 Special exposure cohort study と呼ばれ、他の方法よりも、効率的に仮説検証を行うことができます。
短所②:打ち切り(脱落と競合リスク)の問題
前向きコホート研究の最大の課題は、追跡対象者の脱落や追跡不能の問題です。コホート研究は、通常、長い間、疾病の発生状況を追跡する必要がありますが、必ずデータが取れるとは限りません。現実的には、観察対象者の転居や心境の変化により、連絡がつかなくなってしまうことも十分あり得ます。このように、疾病の発生状況を追えなくなってしまうことを脱落 drop out や追跡不能 lost to follow-up といいます。
これと同様に、目的としている疾病の発生状況が分からなくなる事象がもうひとつあります。それが、競合リスクの問題です。競合リスク competitive risk とは、目的としている疾病以外の原因によって、リスク集団から除外されてしまうことを指し、典型的には、例えば、交通事故や他の疾患などによって観察対象者が死亡してしまう場合がこの競合リスクの問題に当てはまります。
このように、観察が中止されてしまうことを総称して、打ち切り censoring といい、打ち切りの問題があるために、疾病発生情報の妥当性はケース・コントロール研究と比較すると、低くなります。

また、このような打ち切りには、評価指標の算出や解釈を難しくしてしまうという問題もあります。例えば、曝露群と非曝露群をそれぞれ1000人ずつ追跡調査し、5年後、非曝露群は全員に連絡がついて、200人にアウトカムが発生していたとします。これに対し、曝露群では100人にアウトカムが発生していることが確認されましたが、残りのうち、100人は音信不通により脱落、100人が他の要因で死亡してしまっていました。
このとき、非曝露群の発生割合は、
\begin{gather}
{\hat{\pi}}_0=\frac{200}{1000}=0.2
\end{gather}
と問題なく求めることができます。
では、曝露群の発生割合についてはどうでしょうか?
単純にアウトカムの発生が確認できた数を用いて、
\begin{align}
{\hat{\pi}}_1=\frac{100}{1000}=0.1
\end{align}
あるいは、打ち切りが起こった人をすべてアウトカム発生に組み入れて、
\begin{align}
{\hat{\pi}}_1=\frac{300}{1000}=0.3
\end{align}
それとも、打ち切りが起こった人は最初から観察対象ではなかったことにして、
\begin{align}
{\hat{\pi}}_1=\frac{100}{800}=0.125
\end{align}
いろいろな考え方がありますが、どれを採用しようにも、それなりに恣意的であるような気がして、バシッと妥当性のある数字を出すのは難しいように思えます。
こうした打ち切りの問題がある場合は、本稿で見てきたような発生割合を用いるよりも、各対象者の観察時間を考慮した発生率を用いる方が解釈しやすい指標となり、多くの疫学研究では、発生率のほうが優れた指標であり、発生率が求められない場合にのみ、次善の策として発生割合を用いる
$^\mathrm{(1)}$とされています(打ち切りの問題を考慮した分析方法は、生存時間分析と呼ばれていますが、これについては、別稿で詳しく解説します)。
コホート研究において対象者を追跡することは重要で、もし参加者の大部分が追跡中脱落したら、研究の妥当性が脅かされます。疫学の大家、ケネス・ロスマンによれば、対象者の約60%未満しか追跡しないような研究は、たいてい疑いの目でみられる。しかし、脱落した対象者が曝露と疾病の両方に関係した理由で脱落した場合、たとえ70%、80%、いやそれ以上追跡しても、低すぎる
$^\mathrm{(2)}$とされています。
参考文献
- ケネス・ロスマン 著, 矢野 栄二, 橋本 英樹, 大脇 和浩 監訳. ロスマンの疫学. 篠原出版新社, 2013, p.103-127
- スティーブン・ハリー, スティーブン・カミングス ほか 著, 木原 雅子, 木原 正博 訳. 医学的研究のデザイン. メディカル・サイエンス・インターナショナル, 2014, p.101-110
- 丹後 俊郎, 小西 貞則 編集. 医学統計学の事典 新装版. 朝倉書店, 2018, p.85
- 中村 好一 著. 基礎から学ぶ楽しい疫学. 医学書院, 2020, p.55-62
引用文献
- 中村 好一 著. 基礎から学ぶ楽しい疫学. 医学書院, 2020, p.23
- ケネス・ロスマン 著, 矢野 栄二, 橋本 英樹, 大脇 和浩 監訳. ロスマンの疫学. 篠原出版新社, 2013, p.125-126
関連記事
- 医学・疫学研究の基本指標
- 曝露効果の指標
- 選択バイアスと情報バイアス
- 交絡
- 標本抽出法
- 医学・疫学研究デザインの概要
- 横断研究
- ケース・コントロール研究
- 横断研究・コホート研究【有病率・発生割合】(マッチングなし・層化なし)
- 横断研究・コホート研究【有病率・発生割合】(マッチングなし・層化あり)
- 横断研究・コホート研究【有病率・発生割合】(マッチングあり・層化なし)
- 横断研究・コホート研究【有病率・発生割合】(マッチングあり・層化あり)
- コホート研究【発生率】(層化なし)
- コホート研究【発生率】(層化あり)
- コホート研究【生存時間】
- ロジスティック・モデル
- 条件付きロジスティック・モデル
- 一般ロジスティック回帰モデル



0 件のコメント:
コメントを投稿