ケース・コントロール研究は、コホート研究や横断研究と比べると、やや捻った研究デザインとされていますが、状況に応じて適切に行えば、圧倒的に少ないコストでコホート研究と遜色ない結果を得ることができる優秀なデザインです。そんなケース・コントロール研究には、人・時を測定して率や率比を評価するタイプの「密度ケース・コントロール研究」、一定期間における曝露者数を測定し、曝露オッズや曝露オッズ比を評価するタイプの「累積ケース・コントロール研究」、比較的新しい疫学の分析方法である「ケース・コホート研究」などのタイプがありますが、本稿では、最も基本的なタイプである「累積ケース・コントロール研究」について解説しています。
なお、閲覧にあたっては、以下の点にご注意ください。
- スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。
- 曝露(発症)状況を表す右下の添え字は、「0」である場合($n_0,\pi_0$ など)や「2」である場合($n_2,\pi_2$ など)がありますが、どちらも「非曝露群(コントロール群)」を表しています。
ケース・コントロール研究の進め方
観察手順の概要
コホート研究では、観察対象者を曝露群と非曝露群に分けて、前向きに観察し、アウトカムの発生状況を調べていきました。ケース・コントロール研究 case-control study は、それとは逆に、まず、現時点で既にアウトカムが発生している人を集めてきて、ケース群 case group を形成し、続いて、現時点でアウトカムが発生していない人を集めてきてコントロール群 control group を形成します。その後、それぞれの群について、関心のある危険因子に対する曝露の有無や頻度を調べることで曝露と疾病発生の関連を明らかにします。
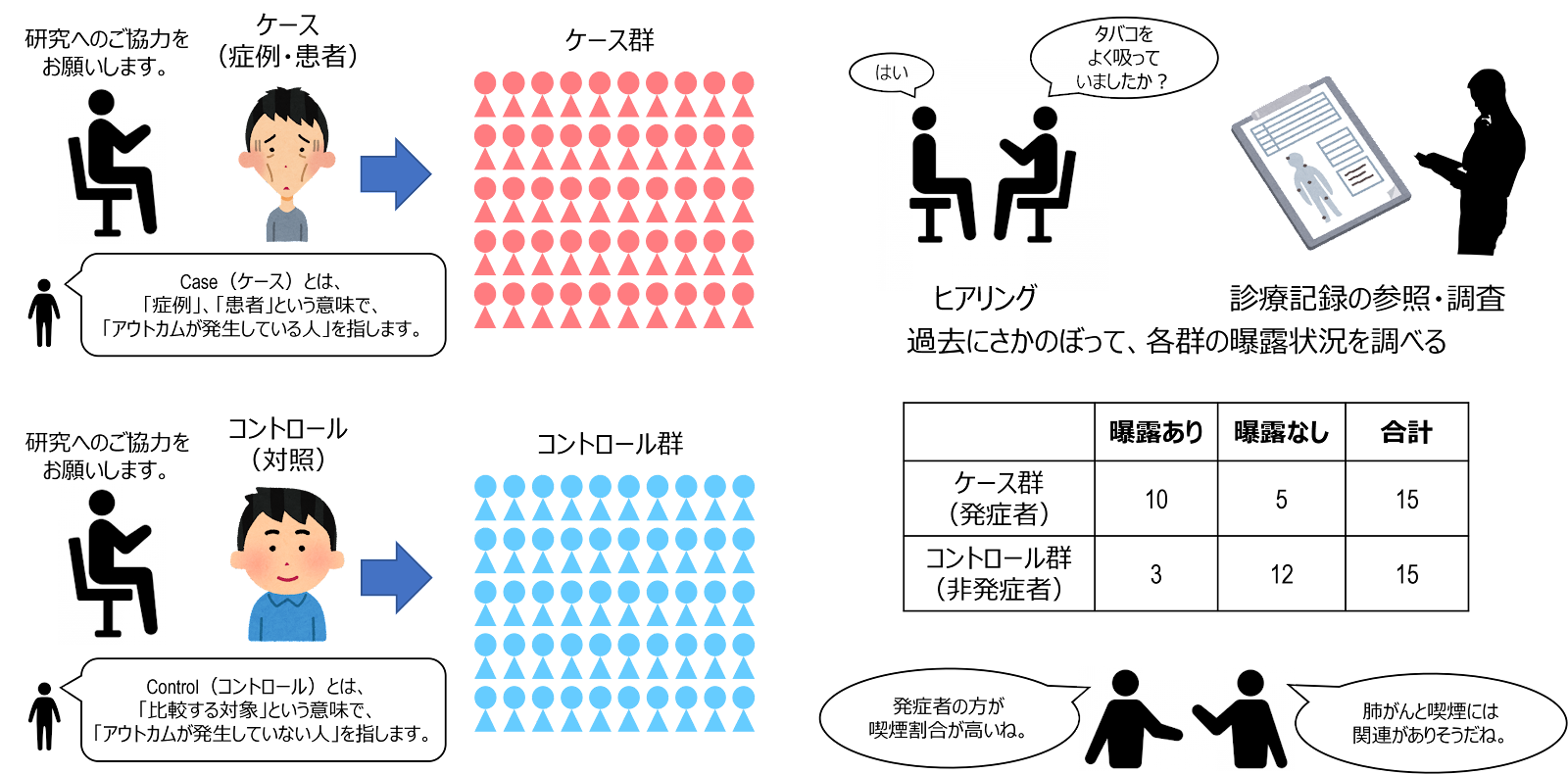
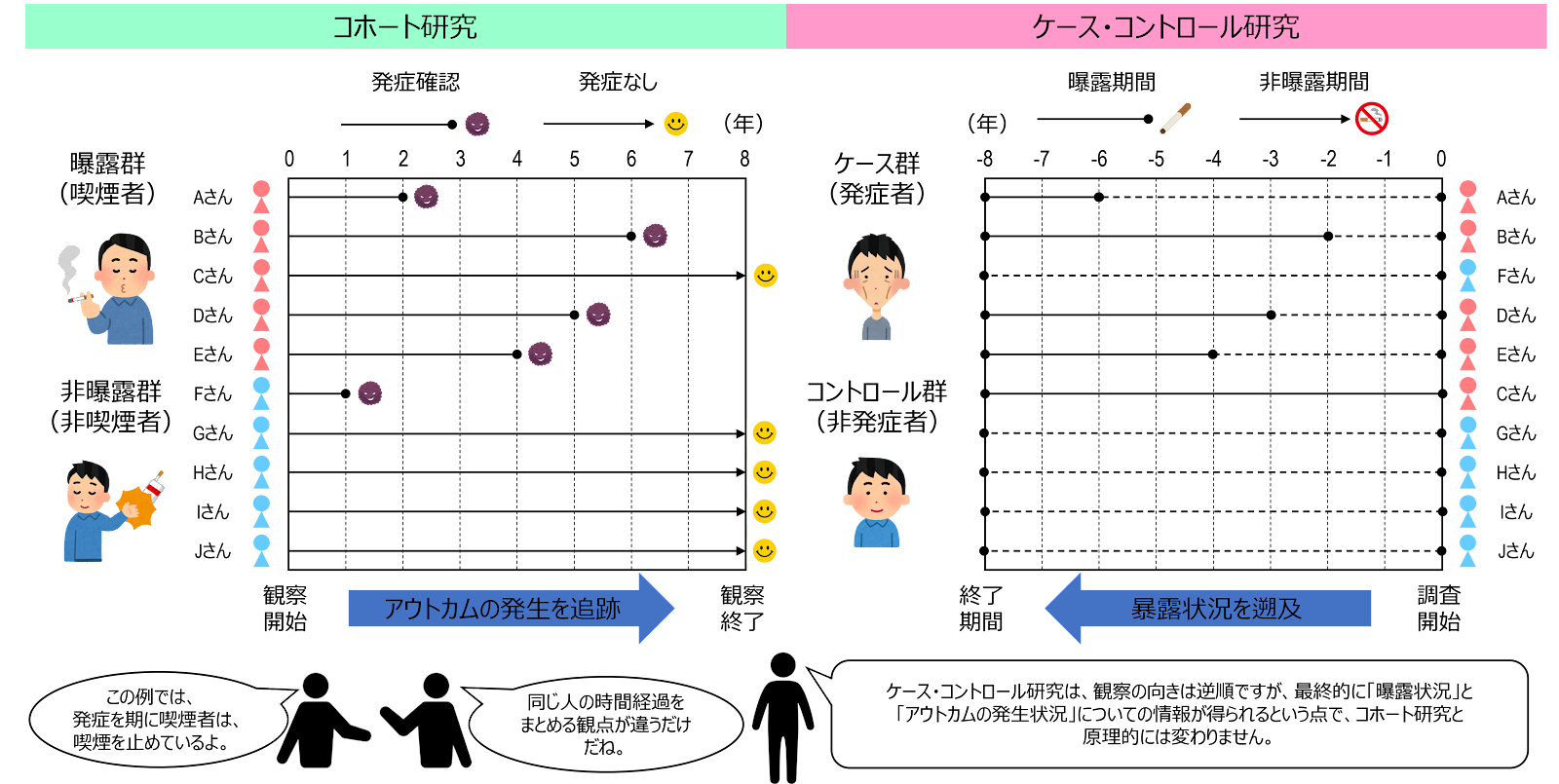
このように、ケース・コントロール研究の観察の方向性は「曝露」←「疾病発生」であり、逆行 back forward、ないし、後ろ向き retrospective と言えます。ただ、最終的に「曝露状況」と「アウトカムの発生状況」についての情報が得られるという点で、コホート研究と原理的には変わりはなく、曝露状況に関する記録がしっかりと取られていれば、コホート研究の情報を完全に再現することができます。
なお、ケース・コントロール研究は、症例対照研究や患者対照研究と呼ばれることもあります。これは、ケース・コントロール研究がもともと、何らかの病気の危険因子を探索するための疫学研究手法として開発され、説明の分かりやすさの観点から、疾病を有する群を “Case”(症例、ないし患者)と呼んできたことが由来です。コントロールとは、科学研究において、結果を検証するための比較対象を意味する言葉です。漢字は「対照」が正しく、「対象」、「対称」と間違えないように気をつけましょう。
コントロール群の選び方
ケース・コントロール研究は、先にも述べたように、「コホート研究を行っていれば観察されたであろう事象を逆順で観察する」という研究デザインです。そのため、ケース・コントロール研究でコントロール群を選ぶ際にも、コホート研究における原集団やリスク集団を意識すると、適切な抽出方法についてのイメージをつかみやすくなります。
例えば、ある時期にある地域で謎の人物が謎の薬を配り歩いていたとします。その人物は、ある日、忽然と姿を消し、現在ではその薬は手に入りません。その後、原因不明の体調不良を訴える人が続出し、「その薬が怪しいのではないか」ということになりました。このとき、ケースは、「原因不明の体調不良となった人」ということになりますが、どういった人をコントロール群とすればいいでしょうか?

このとき、仮に前向きに結果を観察できたとすれば、原集団は、「ある時期にその地域に住んでいた人」と設定することができるでしょう。逆に言えば、例えば、「その時期に、旅行に行っていてまちを離れていた人」や「謎の人物がいなくなった後に、この地域に引っ越してきた人」は、リスクに曝露される可能性がなかったので、原集団からは除外されることが分かります。このように、ケース・コントロール研究におけるコントロール群は、まず、「観察対象とする状況(疾病発生)になっていないが、危険因子に曝露されていた可能性があり、もし、当人にアウトカムが発生したならば症例としてカウントされていたであろう人」、あるいは、「ケースと同じ疾患に罹患するリスクがあり、かつその時点では罹患していないという点以外ではケースと類似している人々」の中から選ぶ必要があります。
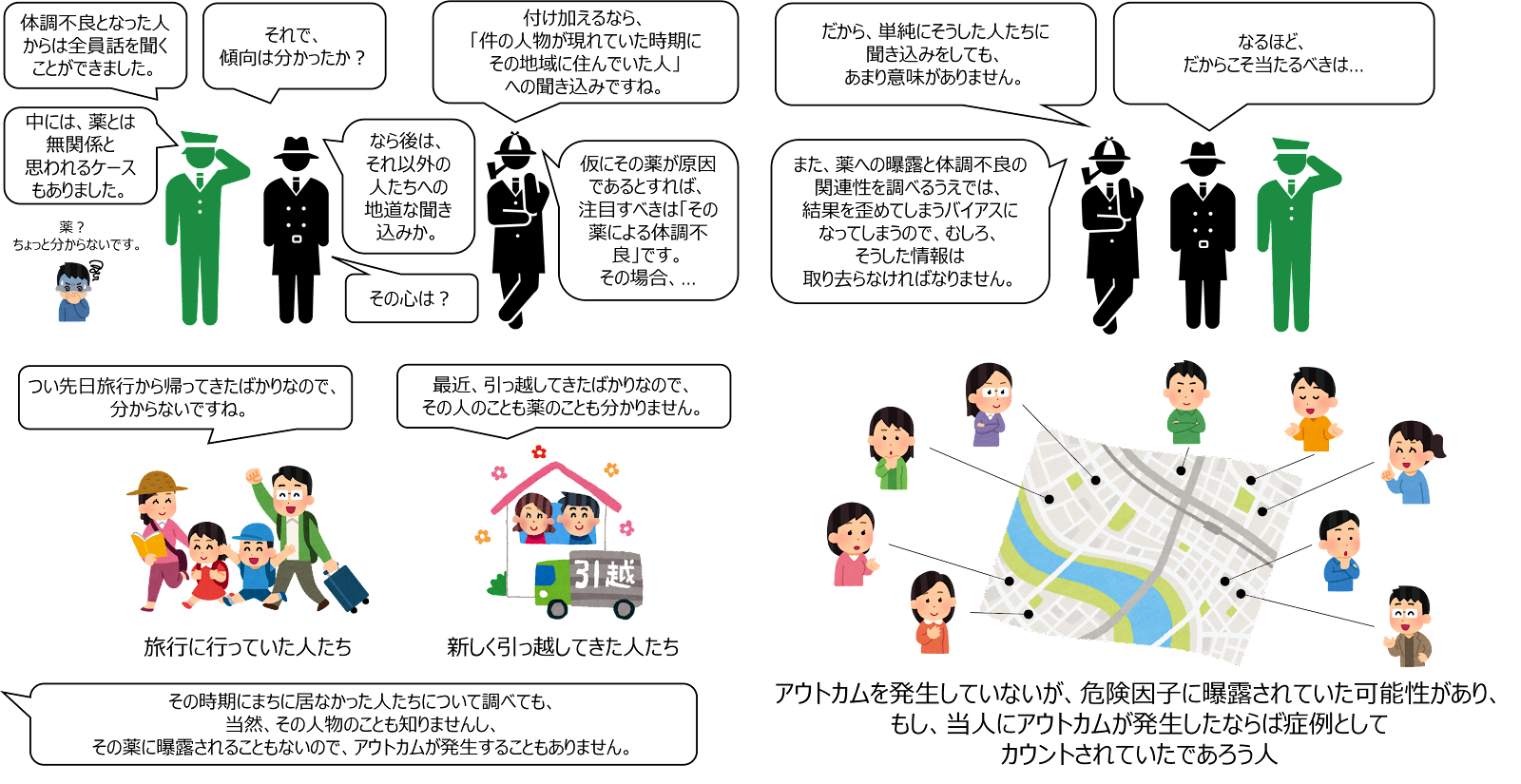
また、「曝露状態と無関係(原集団から無作為)に標本抽出する」ことも必要です。例えば、「体調不良ではなく、薬を飲まなかった人」だけをコントロール群とすれば、当然のことながら、コントロール群の曝露割合は0となりますが、これは、結論ありきの恣意的な操作になってしまいます。もしかしたら、「体調不良にならなかった人の中にも、薬を飲んでいた人は結構いた」、あるいはむしろ、「実は薬が体調不良になることを予防していた」という結果が得られる可能性も否定できません。それゆえに、曝露状況を調べる前に、無作為抽出でコントロール群の設定を行う必要があります。

なお、イベントを発生するのはコホートのごく一部の対象者だけなので、通常はコントロールとして調べるのもイベントを発生しなかった全対象者ではなく、ケースに見合った人数だけランダムにコントロールを選び、ケース群とコントロール群の曝露状況を比較します。
こうした原則を踏まえたうえで、現実の研究においては、次の3種類のコントロール群の設定方法があります。
一般集団対照
一般集団対照 population controls は一般の地域住民(あるいは職域集団の中)から無作為にコントロールを選ぶ方法で、電話(ランダムに生成された電話番号に電話し、条件に合う人が出たら対照となることをお願いする)や住民基本台帳、選挙人名簿などが利用されています。地域がん登録の制度がある場合など、症例が一定地域のすべての患者から成り立っている場合にはこの方法が最も望ましいですが、依頼しても断られる確率が最も高い方法でもあります。
近隣対照
近隣対照 neighborhood controls は症例と同居する家族や隣近所の人をコントロールとするものです。参加率は高いことが期待されますが、そもそもケースとコントロールの背景が近似しており、感染症などの急性疾患の症例対照研究を除き、現在では、あまり用いられていません。
病院対照
病院対照 hospital control は、関心のある疾患以外の疾患を理由に、ある医療機関を受診した人、あるいは治療している人をコントロールとする方法です。実際の臨床研究は、医療機関で行われることが多く、疾患(病気)を研究対象としているので、その医療機関に集まってきてくれる人をコントロールとするこの方法は、効率的かつ現実的に実施しやすい方法です。この方法は、医療圏や患者の受療行動を考えた場合、コントロール群として必要な条件をよく満たし、コントロール群となることを依頼した場合、これに応じてくれる確率も高いことが期待されます。
病院対照の場合、仮にコホート研究として行うとしたときの原集団は、「もしその疾患に罹患したら、その医療機関を受診するであろう人々」と設定するのが一般的です。この点、「その医療機関がある地域住民全体」を原集団と設定することも考えられますが、一般的には、地域のごく一部の人だけを治療していることが多く、必ずしもその地域の住民全体とは一致しません。
極端な例を挙げれば、例えばその病院は中心市街地にあり、周辺地区よりも郊外から通院してくる人が多いとします。また、治療実績は良い反面、医療費は高く、経済的に余裕がなければ受診できない病院だとしましょう。このとき、中心市街地の近くにあるスラム街の人々をコントロールとして選ぶと、そのケース群に設定された人たちとは、背景となる因子(年齢、性別など)の分布にかなりの差があると予想されます。こうした差が極端である場合、横並びでの比較は難しくなってしまいます。この点、「他の疾患を理由にその病院を受診した人」であれば、「研究対象の病気にかかったらその医療機関を受診する人々」にほぼ一致し、背景因子は、そこまで異ならないと期待できます。症例と同じ医療機関で治療を受ける他の患者は、無作為抽出されたものではありませんが、似た背景因子を持つ人々(原集団)の抽出標本となります。
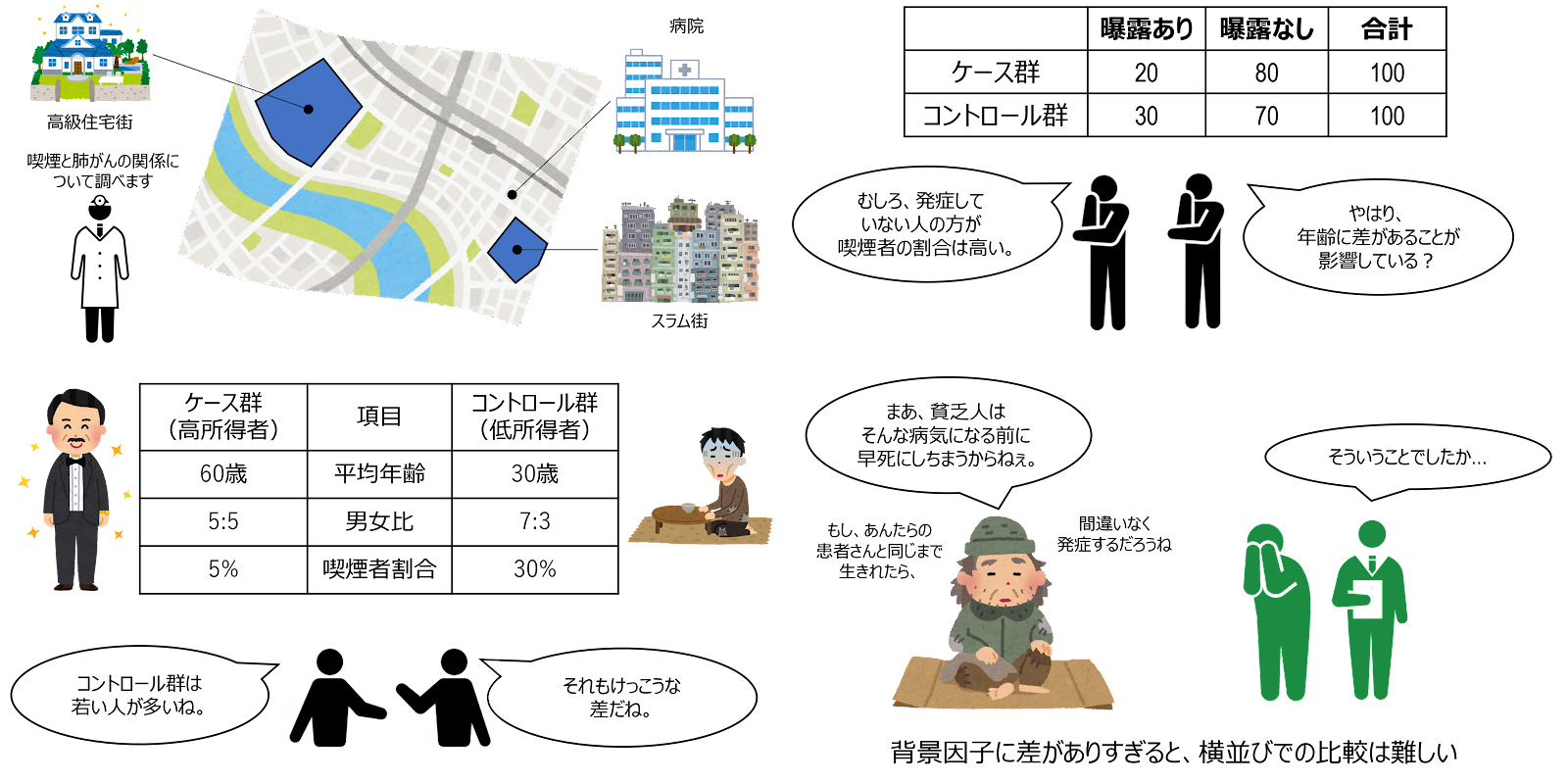
ただ、コントロールを無作為抽出していないために生じる注意点もあります。それは、関心のある因子への曝露割合が一般集団全体と同じでないために、曝露の影響が過小評価、あるいは過大評価される可能性があるという点です。
たとえば、喫煙と白血病の関係を評価することを目的としているとします。他のがん、心血管疾患や呼吸器疾患などさまざまな病気が喫煙と関係していますが、コントロールを「白血病以外の理由で入院した人」とする場合、喫煙を原因とする病気のために入院している人もたくさんいるでしょう。そのため、白血病以外の病気のため入院した人には、一般集団より多い割合で喫煙者がいることになります。
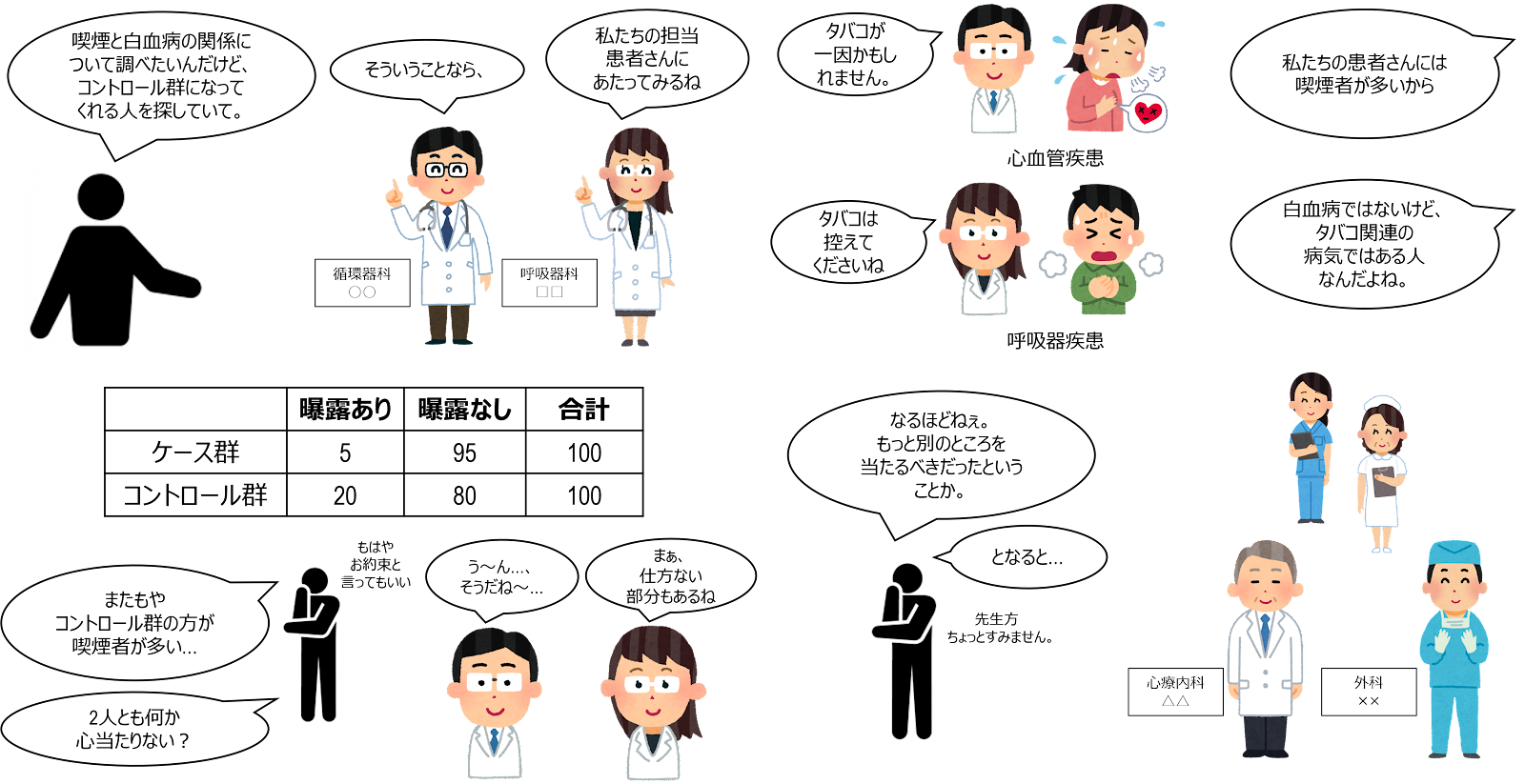
この問題への対策として、曝露と関係ありそうな診断をすべてコントロール群から除外するという方法があります。たとえば、先に考えた喫煙と白血病に関する研究ならば、喫煙に関係あると考えられる病気で入院した人は、コントロール群から除外するということです。この対策では、多くの診断区分を排除することになる可能性がありますが、後述するように、ケース・コントロール研究は、比較的小さいサンプルサイズでも実施できる方法であるため、少ない診断区分からでも十分な数のコントロールを見つける可能性があります。
データの形式と基本指標
分割表の形式
ケース・コントロール研究のデータは、以下のような $2\times2$ 分割表にまとめられます。これは、横断研究やコホート研究の分割表の行と列を入れ替えたかたちをしていますが、曝露に関する合計値のセルが用意されていません。曝露あり・曝露なしの合計人数は、もちろん簡単に求めることはできますが、後述するように、研究者がコントロール群をどれくらい集めるかによって、値が変わってしまい、安定した値にならないので、実用上、算出する意味がない値となっています。
| 曝露あり $ \left(E\right)$ | 曝露なし $(\bar{E})$ | 合計 | |
|---|---|---|---|
| ケース群 $ \left(D\right)$ | $a$ | $c$ | $n_1$ |
| コントロール群 $(\bar{D})$ | $b$ | $d$ | $n_0$ |
曝露割合:リスク(発症割合)を求めることはできない
コホート研究では、曝露群と非曝露群それぞれの発症割合を求め、リスク比やリスク差を算出することで、直感的に理解しやすいかたちで曝露効果を評価することができました。しかし、ケース・コントロール研究では、ケースが由来した母集団や期間がわかっている場合を除き、そもそもリスク(各群の発症割合)を求めることができず、リスク比やリスク差による比較ができません。なぜなら、研究者がケース群とコントロール群をどれくらい集めるかによって、各群の発症割合の推定値が変わってしまうからです。
| 曝露あり $ \left(E\right)$ | 曝露なし $(\bar{E})$ | 合計 | |
|---|---|---|---|
| ケース群 $ \left(D\right)$ | $5$ | $1$ | $6$ |
| コントロール群 $(\bar{D})$ | $95$ | $99$ | $194$ |
| 合計 | $100$ | $100$ | $200$ |
| 曝露あり $ \left(E\right)$ | 曝露なし $(\bar{E})$ | 合計 | |
|---|---|---|---|
| ケース群 $ \left(D\right)$ | $10$ | $2$ | $12$ |
| コントロール群 $(\bar{D})$ | $285$ | $297$ | $582$ |
| 合計 | $295$ | $299$ | $594$ |
例えば、上の表のように、パターン①(標準)のときは、 \begin{gather} {\hat{\pi}}_1=\frac{5}{100}=0.05 \quad {\hat{\pi}}_0=\frac{1}{100}=0.01\\ \mathrm{\widehat{RD}}=0.04\\ \mathrm{\widehat{RR}}=5.0 \end{gather} パターン②(ケース群を2倍、コントロール群を3倍)のときは、 \begin{gather} {\hat{\pi}}_1=\frac{10}{295}\cong0.0339 \quad {\hat{\pi}}_0=\frac{2}{299}\cong0.0067\\ \mathrm{\widehat{RD}}=0.0272\\ \mathrm{\widehat{RR}}=5.068 \end{gather} となり、リスクやリスク比、リスク差の推定値が異なります。
このため、ケース・コントロール研究では、基本的な評価指標として、まず、それぞれの群の曝露割合を求めます。曝露割合は、以下のように定義されます。
\begin{gather} {\hat{\phi}}_1=\frac{a}{n_1} \quad {\hat{\phi}}_0=\frac{b}{n_0} \end{gather}
曝露と疾病の関係性の評価
曝露オッズと曝露オッズ比
先ほど述べたように、ケース・コントロール研究では、リスク比などを直接求めることはできませんが、代わりにオッズ比という指標を求めることで、曝露と疾病の関係性を評価することができます。
オッズ odds とは、特に競馬などでよく使われる言葉である事象が起こらない確率と起こる確率の比を意味します。ケース・コントロール研究においては、それぞれの群の曝露オッズは、以下のように定義されます。 \begin{gather} \mathrm{{\widehat{OD}}_{Retro1}}=\frac{{\hat{\phi}}_1}{1-{\hat{\phi}}_1}=\frac{a}{c} \quad \mathrm{{\widehat{OD}}_{Retro0}}=\frac{{\hat{\phi}}_0}{1-{\hat{\phi}}_0}=\frac{b}{d} \end{gather}
曝露オッズ比 exposure odds ratio とは、各群の曝露オッズの比のことで、標準的には、「コントロール群のオッズを分母、ケース群のオッズを分子」として定義されます。 \begin{gather} \mathrm{{\widehat{OR}}_{Retro}}=\frac{\mathrm{{\widehat{OD}}_{Retro1}}}{\mathrm{{\widehat{OD}}_{Retro0}}}=\frac{ad}{bc} \end{gather}
このオッズ比を用いると、先ほどの例では、パターン①のオッズ比は、 \begin{gather} \mathrm{{\widehat{OR}}_{Retro}}=\frac{5\times99}{95\times1}=5.211 \end{gather} パターン②のオッズ比は、 \begin{gather} \mathrm{{\widehat{OR}}_{Retro}}=\frac{10\times297}{285\times2}=5.211 \end{gather} となりぴったり一致します。 オッズ比は、「無作為に抽出する」、「最低限必要な数以上、サンプリングしている」などの仮定が守られていれば、抽出する人数によらず常に一定の値になるという性質があるため、評価指標として安定しています。
稀少疾病の仮定
相対リスク(リスク比)は、例えばつまり、「タバコを吸っている人が肺がんになる確率」と「タバコを吸っていない人が肺がんになる確率」を比較する指標であるため、単純で分かりやすい指標です。それに対しオッズ比は、「肺がんの人がタバコを吸っていたオッズ」と「肺がんでない人がタバコを吸っていたオッズ」を比較していて、それ自体を解釈しようと思っても、どう解釈していいのかが分かりにくい指標です。
しかし、オッズ比には、「そのアウトカムの有病率が十分小さい(約10%かそれ以下)である場合、リスク比の近似値として用いることができる」という性質があることが知られています。これを稀少疾病の仮定 rare disease assumption や稀なイベントの仮定 rare event assumption といい、稀少疾病の仮定が成り立つ状況では、曝露オッズ比=発症リスク比と読み替えて、解釈することができます。
例えば、「肺がんの喫煙に関する曝露オッズ比が5.0である」ということは、稀少疾病の仮定の下では「喫煙すると喫煙しないときと比べて、肺がんになる確率が5倍になる」ということと同じであり、喫煙と肺がんの関連性を示すという目的は十分に果たすことができます。
また、稀少疾病の仮定は、累積ケース・コントロール研究の場合には必須ですが、密度ケース・コントロール研究では、必ずしも必要ではありません。密度ケース・コントロール研究では、疾病の有病率が高くても、バイアスのない率比の推定値が得られるとされています。ただ、累積ケース・コントロール研究で稀少疾病の仮定が当てはまる場合、リスク比は率比に近似し、オッズ比、リスク比、率比はすべてほぼ同じ値になるとされています。
ケース・コントロール研究の特徴
長所①:結果を得るためのコストが少なく、特に稀な疾患(事象)の場合に向いている
ケース・コントロール研究における最大の利点は、比較的少ない対象者から迅速にかつ多くの情報が得られることです。たとえば、出生時に行われる儀式とがんの発症に関する研究$^\mathrm{(1)}$の場合を考えてみましょう。このがんの生涯累積発生率 lifetime cumulative incidence は約0.16%であるため、曝露群と非曝露群がほぼ半々であるとして、コホート研究で80%の検出力でその関連を検出するには、リスク比が50の非常に強いリスクファクターであっても計算上6000人以上もの対象者が必要となります。いっぽう、その儀式への曝露効果をランダム化比較試験で検討しようとすると、これと同数の対象が必要となるばかりか、そのがんの平均的な発病年齢は67歳であるため、その対象者をフオローアップするためには、疫学者が3世代にもわたって調査しなくてはならない計算になります。
これに対し、同じ問題をケース・コントロール研究で行う場合は、先程と同じリスク比(相対リスク)を同じ感度で検出するには、わずか16人の患者と16人のコントロールで済むことになり、研究に要する時間もはるかに短くて済みます。このように、たとえば、稀な疾患、あるいは曝露から発病までの潜伏期間が長い疾患の場合は、ケース・コントロール研究が最適の方法であり、事実、この方法だけが唯一実施可能な方法となります。
なお、稀少疾病の仮定が成り立たない場合、近似の精度が悪くなり、一般的に「オッズ比>相対危険度」となるため、曝露効果の危険性を過大評価しやすくなります。このため、こうした場合には、オッズ比を用いるケース・コントロール研究よりも、より直接的に関連性(リスク比)を示すことのできるコホート研究でリスク比を算出する方が良いといえます。
また、曝露の方が稀な場合は、大量のケースとコントロールが必要となり、研究の効率が悪くなるので、そうした場合も前向きコホート研究を行う方が良いとされています。
長所②:1つの疾病に関連する異なる曝露要因を多数検討するのに便利
ケース・コントロール研究は、分析の対象とできるアウトカムは1つだけですが、対象とできる危険因子は複数設定できるため、1つの疾病に関連する異なる曝露要因を多数検討するのに便利なことが多い研究方法です。
特に、新たに集団発生した疾患(食中毒や急性疾患など)の病因について調べたい場合など、前向きに検証することが原理的にできないこともありますが、こうした場合に、ケース・コントロール研究は、一度に数多くの因子と疾患の関連を調べることができるため、効率的に原因究明を行うことができます。

たとえば、ハイチの子どもたちにおける急性腎不全の流行に関するケース・コントロール研究では、現地で製造されたアセトアミノフエンシロップの使用に対して53という非常に高いオッズ比が確認されました。その後、腎不全の原因は、アセトアミノフエンシロップ製造時に使用するグリセリン溶液を汚染した$^\mathrm{(2)}$ジエチレングリコールであることが明らかにされています$^\mathrm{(3)}$。
短所:バイアスの影響を受けやすい
ケース・コントロール研究の最大の欠点は、バイアスの影響を受けやすいことです。バイアスが入り込むチャンスは大きく2つあり、1つはケース群とコントロール群が別々に選び出される過程(サンプリング・バイアス)と、もう1つは予測因子の測定が過去に遡って行われる過程(測定バイアス)です。
サンプリング・バイアスは、先に「コントロール群の選び方」で挙げたように、ケースが発生した集団と異なった集団からコントロールをとることにより、正しい比較ができなくなってしまうことです。
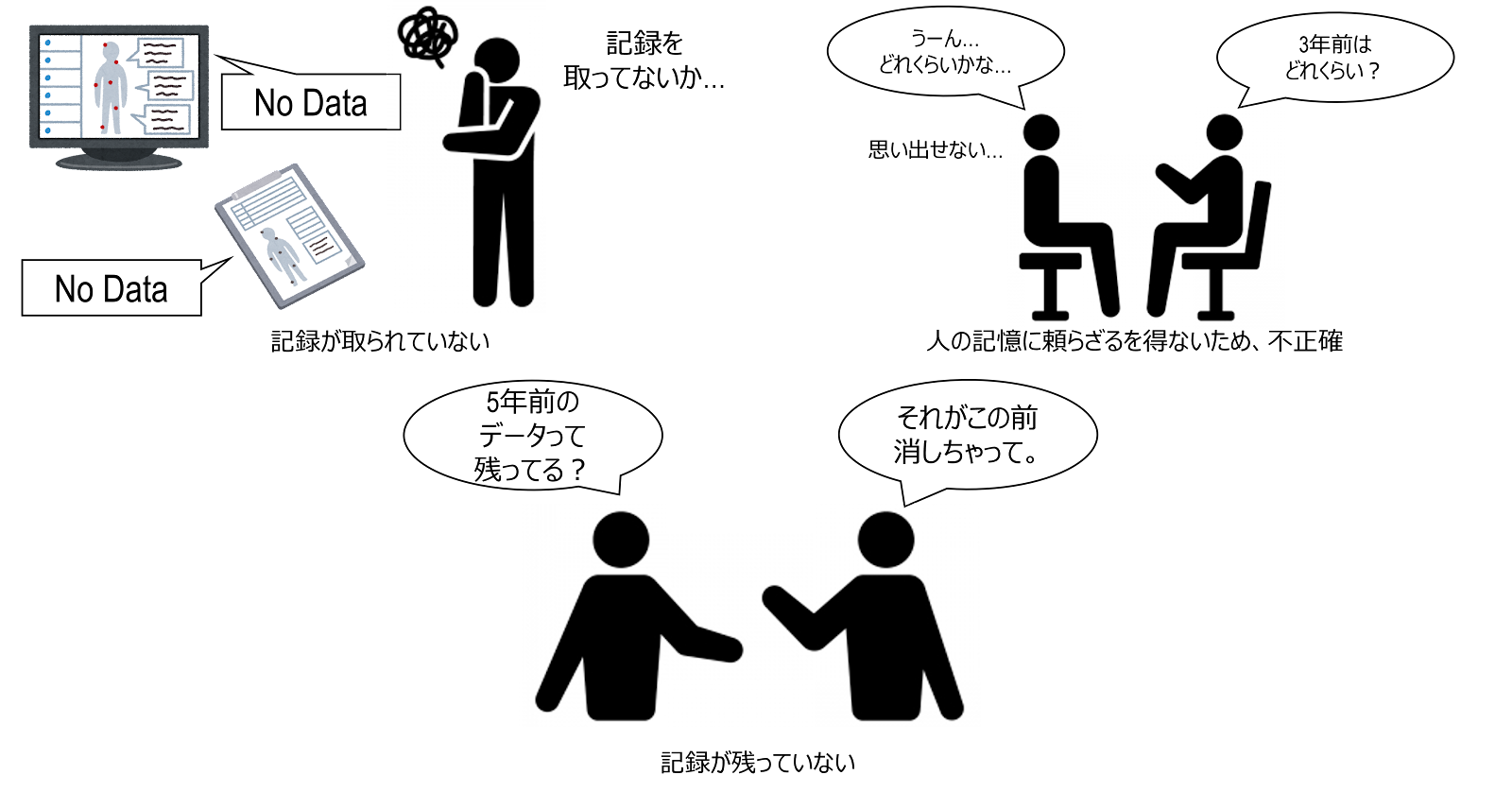
測定バイアスは、例えば、記録書類が紛失していたり、そもそも記録が取られていなかったりということや、聞き取り調査において、情報の質を対象者の記憶に頼らざるを得ないため、情報が不正確だったり、曖昧だったりすることです。こうしたことは、前向きコホート研究では、予防することができるため、ケース・コントロール研究に特有の問題点といえます。
参考文献
- ケネス・ロスマン 著, 矢野 栄二, 橋本 英樹, 大脇 和浩 監訳. ロスマンの疫学. 篠原出版新社, 2013, p.128-147
- スティーブン・ハリー, スティーブン・カミングス ほか 著, 木原 雅子, 木原 正博 訳. 医学的研究のデザイン. メディカル・サイエンス・インターナショナル, 2014, p.112-131
- 丹後 俊郎, 松井 茂之 編集. 医学統計学ハンドブック. 朝倉書店, 2018, p.501-508
- 丹後 俊郎, 小西 貞則 編集. 医学統計学の事典 新装版. 朝倉書店, 2018, p.85-86
- 中村 好一 著. 基礎から学ぶ楽しい疫学. 医学書院, 2020, p.63-70
引用文献
- Kochen, M. & McCurdy, S.. Circumcision and the Risk of Cancer of the Penis: A Life-Table Analysis. American journal of diseases of children. 1980;134(5):484-486, doi: 10.1001/archpedi.1980.02130170034012
- O{\prime}Brien, K.L., Selanikio, J.D., Hecdivert, C. et al.. Epidemic of pediatric deaths from acute renal failure caused by diethylene glycol poisoning. Acute Renal Failure Investigation Team. Journal of the American Medical Association. 1998;279(15):1175-1180, doi: 10.1001/jama.279.15.1175
- Centers for Disease Control and Prevention. Fatal poisoning among young children from diethylene glycol-contaminated acetaminophen - Nigeria, 2008-2009. MMWR Morb Mortal Wkly Rep. 2009;58(48):1345-1347



0 件のコメント:
コメントを投稿