曝露効果の指標

疫学研究では、ある因子への曝露と疾病の発生頻度の因果関係を推論する際、リスク差やリスク比などの曝露効果の指標にもとづいて判断します。本稿では、そうした疫学の基本的な曝露効果の指標であるリスク差やリスク比、NNT、寄与危険割合、集団寄与危険割合などについて解説しています。

なお、閲覧にあたっては、以下の点にご注意ください。

• スマートフォンやタブレット端末でご覧の際、数式が見切れている場合は、横にスクロールすることができます。

 

複数の集団における頻度の比較

ある因子への曝露がアウトカムの発生確率を高めるか否かを調べる場合、曝露群と非曝露群における「リスク＝疾病の頻度」を比較します。「リスク」は、広義には、発生割合と発生率、狭義には発生割合のみを指す言葉として用いられており、人ごとに意味が異なるため、注意が必要となります。

本稿では、曝露群と非曝露群の発生割合をそれぞれ \begin{gather} \mathrm{R_0} \left(=\pi_0\right) \quad \mathrm{R_0} \left(=\pi_1\right) \end{gather} 発生率をそれぞれ \begin{gather} \mathrm{IR_0} \quad \mathrm{IR_1} \end{gather} とおき、 コホート研究のデザインにならい、発生割合が以下のような表にまとめられるとします。

表1 曝露・発症状況に関する分割表（統計モデル）

	発症あり $ \left(D\right)$	発症なし $(\bar{D})$	合計
曝露群 $ \left(E\right)$	$\pi_1$	$1-\pi_1$	$1$
非曝露群 $(\bar{E})$	$\pi_0$	$1-\pi_0$	$1$

相対的効果指標

リスク比

曝露群と非曝露群の発生割合の比を（狭義の）相対リスク relative risk、あるいはリスク比 risk ratio と呼びます。理論上、取り得る値の範囲は、0以上の値すべてで、単位や次元はありません。 \begin{align} \mathrm{RR}=\frac{\mathrm{R_1}}{\mathrm{R_0}}\in \left[0,\infty\right] \end{align}

発生率比

曝露群と非曝露群の発生率の比を発生率比 incidence rate ratio と呼びます。理論上、取り得る値の範囲は、0以上の値すべてで、単位や次元はありません。 \begin{align} \mathrm{IRR}=\frac{\mathrm{IR_1}}{\mathrm{IR_0}}\in \left[0,\infty\right] \end{align}

指標の意味

リスク比は、曝露の相対的な効果を表すもので、曝露と疾病の関連性や因果関係を知りたいときに用いられます。曝露とアウトカムが無関係のとき、リスク比は1になり、非曝露群に対する曝露群の相対危険が大きいほど、関連が強いということを意味します。

また、リスク比を計算することで、「リスク因子があると感染発生確率が何倍になるのか」あるいは「予防対策を行うと感染を何分の1に減らせるのか」といった具体的な曝露効果を推定し、表現することができます。たとえば、喫煙と肺がんの関係において相対危険は通常、4～10程度といわれていますが、これは「非喫煙群と比較して喫煙群では肺がんの頻度が4～10倍高い」という意味です。

絶対的効果指標

リスク差

曝露群と非曝露群の発生割合の差をリスク差 risk difference、あるいは、寄与リスク attributable risk と呼びます。理論上、取り得る値の範囲は、-1以上1以下の値で、単位や次元はありません。 \begin{align} \mathrm{RD}=\mathrm{R_1}-\mathrm{R_0}\in \left[-1,1\right] \end{align}

発生率差

曝露群と非曝露群の発生率の差を発生率差 incidence rate difference、あるいは、寄与率 attributable rate と呼びます。理論上、取り得る値の範囲は、すべての実数で、単位は $ \left[\mathrm{/time}\right]$ です。 \begin{align} \mathrm{IRD}=\mathrm{IR_1}-\mathrm{IR_0}\in \left[-\infty,\infty\right] \end{align}

指標の意味

リスク差は、曝露の絶対的な効果、あるいは、曝露によるリスクの変化量を表すもので、曝露が与える集団への負荷の大きさを測りたいときによく用いられます。曝露とアウトカムが無関係のとき、リスク差は0になります。

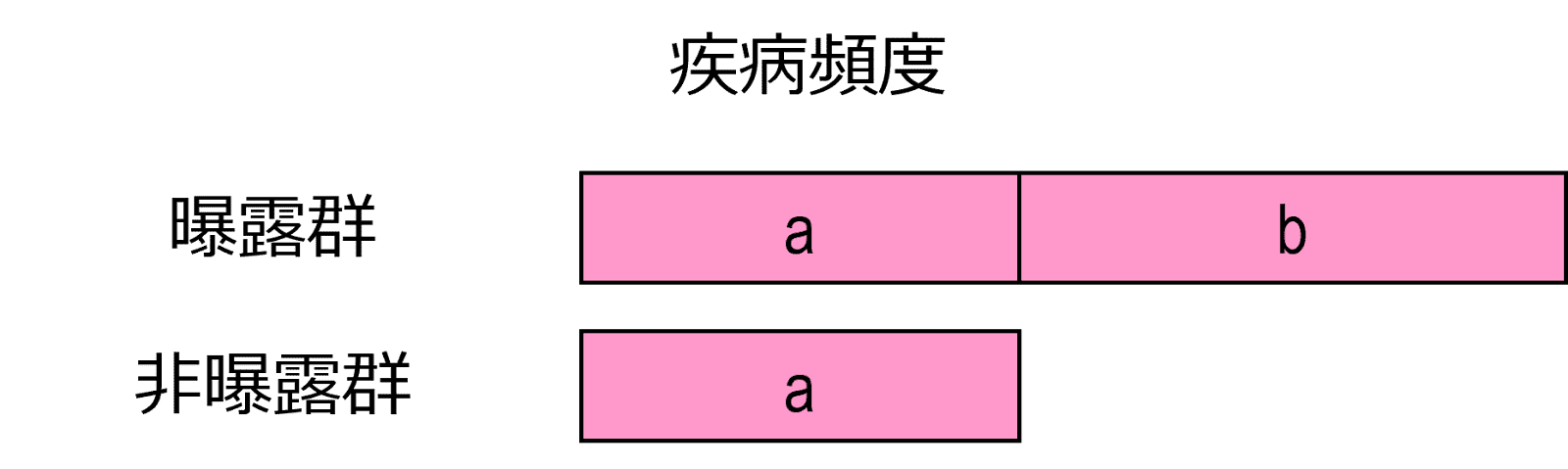
ここで、図のように、 \begin{gather} \mathrm{R_1}=a+b\\ \mathrm{R_0}=a \end{gather} とすると、 $b$ に相当する部分がリスク差ということになります。このとき、曝露群の頻度 $a+b$ のうち、非曝露群の頻度である $a$ の部分は、非曝露群でもこの程度は発生しているのだから、曝露による影響ではないと考えるのが妥当です。そうすると、$b$ の部分に相当するリスク差が、真に曝露によって増加した疾病頻度ということになります。

NNT

リスク差の逆数を NNT:Number Needed to Treat と呼びます。 \begin{align} \mathrm{NNT}=\frac{1}{\mathrm{RD}} \end{align}

例をあげると、仮に、曝露群と非曝露群のリスクがそれぞれ、 \begin{align} \mathrm{R_0}=0.3 \left(30\%\right) \quad \mathrm{R_1}=0.4 \left(40\%\right) \end{align} であった場合、 リスク差は \begin{align} \mathrm{RD}=0.4-0.3=0.1 \end{align} となります。 リスク差が0.1ということは、この要因への曝露を取り除く（予防する）ことができれば、発症者の10人に1人を救うことができるということになります。さらに、この発症を1件減らすためには、曝露予防対策を10人に実施する必要があるということも、リスク差の逆数をとることで簡単に計算できます。 \begin{align} \mathrm{NNT}=\frac{1}{0.1}=10 \end{align} このように、NNTは、介入策の臨床的価値を判断する指標として重要視されています。

寄与危険割合

曝露群の疾病頻度のうちで、真に曝露によって増加した部分の占める割合を寄与危険割合 attributable risk percent、または、寄与分画 attributable fraction と呼びます。 \begin{align} \mathrm{ARP}=\frac{\mathrm{RD}}{\mathrm{R_1}} \end{align} 例えば、曝露群と非曝露群のリスクが先ほどのNNTのときと同様であった場合、 \begin{align} \mathrm{ARP}=\frac{0.1}{0.4}=0.25 \end{align} これは、「曝露によって真に増加している部分は、曝露群全体の25%である」ということを意味しています。特に、曝露とアウトカムの因果関係が認められる場合には、「曝露群での発症の25%は曝露を原因とするものである」と解釈されます。

寄与危険割合は上記の方法で計算するのがオリジナルな考え方ですが、曝露群と非曝露群の疾病頻度が明らかでないと計算できません。ただ、定義式を変形すると、 \begin{align} \mathrm{ARP}&=\frac{\mathrm{R_1}-\mathrm{R_0}}{\mathrm{R_1}}\\ &=\frac{\mathrm{R_1}}{\mathrm{R_1}}-\frac{\mathrm{R_0}}{\mathrm{R_1}}\\ &=1-\frac{\mathrm{R_0}}{\mathrm{R_1}}\\ \end{align} ここで相対リスクの定義式 $\mathrm{RR}=\frac{\mathrm{R_1}}{\mathrm{R_0}}$ より、 \begin{align} \mathrm{ARP}&=1-\frac{1}{\mathrm{RR}}\\ &=\frac{\mathrm{RR}-1}{\mathrm{RR}} \end{align} となります。 つまり、曝露群と非曝露群の疾病頻度が分からなくても、相対リスクが判明していれば寄与危険割合は計算できるということです。この関係は、曝露群・非曝露群の疾病頻度を求めることができないケース・コントロール研究でも、いきなり相対リスクを用いれば、寄与危険割合は求めることができる、という点で大切な関係式です。

集団寄与危険割合

上述の寄与危険、および寄与危険割合の「曝露群の疾病頻度」を「一般集団の疾病頻度」に置き換えたものを、集団（または、人口）寄与危険 population attributable risk、および、集団（または、人口）寄与危険割合 population attributable risk percent と呼びます。集団寄与危険割合は、集団寄与分画 population attributable fraction と呼ぶこともあります。

母集団全体における曝露者と非曝露の割合をそれぞれ \begin{align} \alpha_1 \quad \alpha_0=1-\alpha_1 \end{align} 曝露群、非曝露群、全体の発症確率をそれぞれ \begin{gather} \pi_1 \quad \pi_0\\ \pi_{\bullet }=\alpha_1\pi_1+\alpha_0\pi_0 \end{gather} とします。

表2 集団寄与危険割合の分割表

	発症あり $ \left(D\right)$	発症なし $(\bar{D})$	合計
曝露群 $ \left(E\right)$	$\alpha_1\pi_1$	$\alpha_1 \left(1-\pi_1\right)$	$\alpha_1$
非曝露群 $(\bar{E})$	$\alpha_0\pi_0$	$\alpha_0 \left(1-\pi_0\right)$	$\alpha_0$
合計	$\pi_{\bullet }$	$1-\pi_{\bullet }$	$1$

このとき、集団寄与危険割合は、以下で定義されます。 \begin{align} \mathrm{\mathrm{PAR}}&=\frac{\alpha_1\pi_1-\alpha_1\pi_0}{\alpha_1\pi_1+\alpha_0\pi_0}\\ &=\frac{\alpha_1 \left(\pi_1-\pi_0\right)}{\pi_{\bullet }}\\ &=\frac{\pi_{\bullet }-\pi_0}{\pi_{\bullet }}\\ &=\frac{\alpha_1 \left(\mathrm{\mathrm{RR}}-1\right)}{1+\alpha_1 \left(\mathrm{\mathrm{RR}}-1\right)}\\ &=\frac{\alpha_1 \left(\mathrm{\mathrm{RR}}-1\right)}{\alpha_1\mathrm{\mathrm{RR}+} \alpha_2} \end{align}

指標の意味

集団寄与危険は「一般集団における、曝露によって増加した疾病頻度」、あるいは、「一般集団がすべて非曝露群という理想的な状態であったら、どの程度、疾病頻度を減少させることができるか」という指標です。例えば、「もし母集団において、喫煙が完全になくなるとしたら。肺がんによる死亡がなくなる割合はどのくらいか」という質問に答えることができます。

集団寄与危険割合は、疫学的な実用上、寄与危険割合を考えるだけでは不十分であることから考案されました。すなわち、寄与危険割合は、母集団における曝露の割合を考慮していないため、公衆衛生への全体的な影響の視点が欠けているという点です。

例えば、非曝露群と曝露群のリスクがそれぞれ \begin{align} \pi_1=0.9 \quad \pi_0=0.05 \end{align} であるとします。 つまり、曝露したら、ほとんどの場合でアウトカムが発生するということです。
このとき、寄与危険割合は、 \begin{align} \mathrm{ARP}=\frac{0.85}{0.9}=0.94 \end{align} すなわち、「曝露群での発症の約94%は曝露を原因とするものである」となるため、曝露への対策が重要だと思えます。

しかし、実はその因子に曝露されること自体が稀で、全体における曝露者と非曝露者の割合が \begin{align} \alpha_1=0.001 \quad \alpha_0=0.999 \end{align} である場合はどうでしょう。 ここで、集団寄与危険割合を求めると、まず、全体における発症者の割合は、 \begin{align} \pi_{\bullet }&=\alpha_1\pi_1+\alpha_0\pi_0\\ &=0.001\times0.9+0.999\times0.05\\ &=0.05085 \end{align} 集団寄与危険は、 \begin{align} \alpha_1 \left(\pi_1-\pi_0\right)=0.001\times0.85=0.00085 \end{align} よって、集団寄与危険割合は、 \begin{align} \mathrm{PAR}&=\frac{\alpha_1 \left(\pi_1-\pi_0\right)}{\pi_{\bullet }}\\ &=\frac{0.00085}{0.0585}\\ &=0.0167 \end{align} つまり、曝露を完全に防いだとすると、発症者全体の約1.67%の発症を防ぐということになります。

いっぽう、 \begin{gather} \pi_1=0.3 \quad \pi_0=0.1\\ \alpha_1=0.7 \quad \alpha_0=0.3 \end{gather} の場合はどうでしょう。 つまり、曝露しても発症する確率はそこまで高くないけど、とにかく曝露されている人が多いという状況です。
このとき、各値は、 \begin{align} \mathrm{ARP}=\frac{0.2}{0.3}=0.67 \end{align} \begin{align} \pi_{\bullet }&=\alpha_1\pi_1+\alpha_0\pi_0\\ &=0.7\times0.3+0.3\times0.1\\ &=0.24 \end{align} \begin{align} \alpha_1 \left(\pi_1-\pi_0\right)=0.7\times0.2=0.14 \end{align} \begin{align} \mathrm{PAR}&=\frac{\alpha_1 \left(\pi_1-\pi_0\right)}{\pi_{\bullet }}\\ &=\frac{0.14}{0.24}\\ &=0.58 \end{align} つまり、曝露を完全に防いだとすると、発症者全体の約58%の発症を防ぐということになります。

これら2つの例を比べて見ると、予防のための曝露対策をした場合、後者の方が、効率が良いことが分かります。これが、「母集団における曝露の割合を考慮した結果」です。

相対リスクという用語

先述したように相対リスクは、狭義には「曝露群と非曝露群の発生割合の比」を指す言葉ですが、医学・疫学研究では、しばしば、「リスク」がより広い意味でとらえられ、一般的な用語 generic term として用いられます。例えば、ケース・コントロール研究では、オッズ比 odds ratio、コホート研究で発生率を求めた場合には、発生率比 incidence rate ratio、生存時間分析では、ハザード比 hazard ratio といった具合です。これらの総称が「相対リスク」とされているため、単に「相対リスク」というとどのような指標なのかがあいまいになってしまう可能性があります。そのため、個別の観察や研究結果で述べる場合には、「相対リスク」は用いずに、実際にそこで観察した、たとえばオッズ比などの具体的な観察値の名称を用いた方が良いとされています。

 

参考文献

• ケネス・ロスマン 著, 矢野 栄二, 橋本 英樹, 大脇 和浩 監訳. ロスマンの疫学. 篠原出版新社, 2013, p.87-99
• ジョン・ラチン 著, 宮岡 悦良 監訳, 遠藤 輝, 黒沢 健, 下川 朝有, 寒水 孝司 訳. 医薬データのための統計解析. 共立出版, 2020, p.20-21, p.53-58
• 中村 好一 著. 基礎から学ぶ楽しい疫学. 医学書院, 2020, p.27-35